



read more








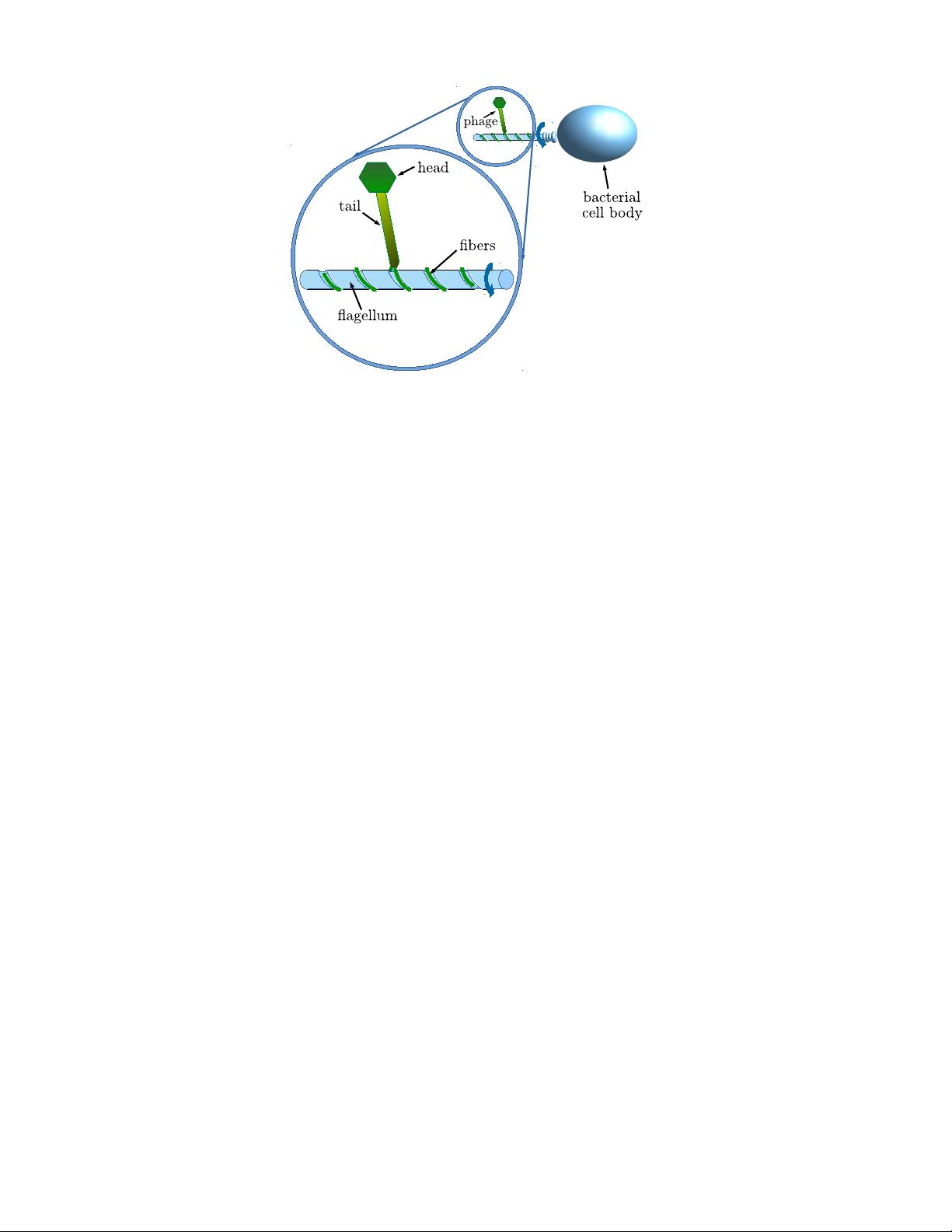
![FIG. 2. Flagellotropic phages: (A) Attachment of phage OWB to V. parahaemolyticus [19]. Red arrows indicate phage particles. (B) Phage PBS1 adsorbed to the flagellar filament of a B. Subtilis bacterium with its tail fibres wrapped around the flagellar filament in a helical shape with a pitch of 35 nm [20]. The phage hexagonal head capsid measures 120 nm from edge to edge [21]. Reprinted (amended) by permission from American Society for Microbiology from Raimondo LM, Lundh NP, Martinez RJ, “Primary Adsorption Site of Phage PBS1: the Flagellum of Bacillus”, J. Virol., 1968, 2 (3), 256-264, Copyright 1968, American Society for Microbiology. (C) χ-phage of E. coli [22]. The head measures 65 to 67.5 nm between the parallel sides of the hexagon [22]; (D) χ-phage at different times between attachment on the flagellar filament of E. coli and reaching the base of the filament [22]. Arrows point to the bases of the flagella. Panels C-D: Reprinted (amended) by permission from American Society for Microbiology from Schade SZ, Adler J, Ris H, “How Bacteriophage χ Attacks Motile Bacteria”, J. Virol., 1967, 1 (3), 599-609, Copyright 1967, American Society for Microbiology.](/figures/fig-2-flagellotropic-phages-a-attachment-of-phage-owb-to-v-2a529nsf.png)
![FIG. 3. Bacterial flagellar filaments and polymorphism: (A) Structure of straight flagellar filament from a mutant of Salmonella typhimurium [24]. Reprinted with permission from O’Brien EJ, Bennett PM, “Structure of straight flagella from a mutant Salmonella”, J. Mol. Biol., 70 (1), 145-152, Copyright 1972 Elsevier. The L-type straight flagellar filament (left) has two types of helical grooves, left-handed long-pitch and right-handed short-pitch grooves, whereas the R-type straight filament (right) has right-handed long-pitch and left-handed short-pitch grooves. Examples of short-pitch grooves are marked by thin blue lines and indicated by arrows. (B) Schematic of some polymorphic states of the flagellar filament, from left to right: L-type straight, normal (left-handed shape), curly (right-handed) and R-type straight. The top panel shows the shape of the filaments while the bottom panel displays the arrangements of flagellin subunits. Examples of short-pitch grooves are marked by thin blue lines and indicated by arrows [25]. Reprinted with permission from Namba K, Vonderviszt F, “Molecular architecture of bacterial flagellum”, Q. Rev. Biophys., 1997, 30 (1), 1-65, Copyright 1997 Cambridge University Press.](/figures/fig-3-bacterial-flagellar-filaments-and-polymorphism-a-2hjcp5ba.png)
This opens up the possibility of a competition between the nut-and-bolt translocation effect and the possibly opposing drag due to translation, which will vary with the helical angle of the flagellar filament. Future studies could address the transient period of wrapping, where the length of the fibres wrapped around the filament is increasing and the ‘ grip ’ is possibly becoming tighter. The authors hope that the modelling developed in this paper will motivate not only further theoretical studies along those lines but also more experimental work clarifying the processes involved in the wrapping and motion of the fibre in the grooves.
The presence of the term involving Lfib in the denominator of Eq. 63 leads to a decrease of U with Lfib, and is physically due to an increase of the viscous drag on the fibres as Lfib increases.
the very drag anisotropy that allows the rotation of helical flagellar filaments to propel bacteria in the bulk will also enable the rotation of helical fibres around a smooth filament to lead to translocation along the axis of the filament.
The common prefactor in the formulae for the translocation speed along the filament, U ∼ −hωflRfl sinα cosα, appears in the expressions from both models.
The authors implicitly capture the effect of the grooves (i) by imposing that the fibres that emanate from the bottom of the tail of the phage are wrapped around the flagellar filament in a helical shape and (ii) via the anisotropy in the drag arising from the relative motion between the fibres and the rotating flagellar filament.
The assumption of a helical wrapping of the fibres coupled with this anisotropy simulates the guiding effect of the grooves in this first model by resisting motion perpendicular to the local tangent of the grooves and promoting motion parallel to it.
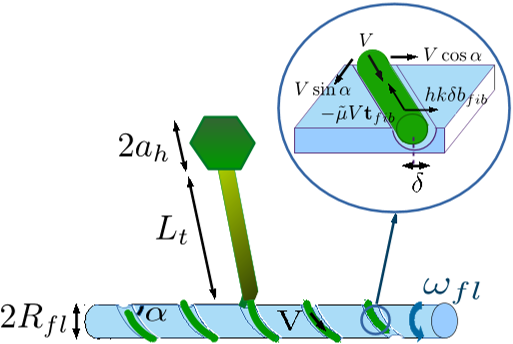
A simple modelling approach consists of viewing each side13of the groove as repelling the fibre, with the resultant of these forces providing a restoring force hkδbfib(s) per unit length, arising from a potential well 12kδ2 where δ is the distance from the centre of the well, and bfib is the local binormal vector to the fibre centreline,bfib =[ h cosα sin ( sRfl/ sinα) ,− cosα cos ( sRfl/ sinα) , h sinα ] , (44)that lies in the local tangent plane of the surface of the flagellar filament and is perpendicular to the tangent vector tfib of the fibre centreline.
The drag force and torque due to the motion of the head in the otherwise stagnant fluid are given byFhead = −6πµahurelhead, (13) ez ·Mhead = ez · [ −6πµah ( rh ∧ urelhead )] − 8πµa3hωp, (14)8 with urelh given byurelh = ωp (ez ∧ rh) + Uez. (15)Taking th = ttail, the centre of the head will be located at position rh = rb +
5. With the assumption that the gap between the fibres and the flagellar filament is negligible compared to the radius Rfl of the flagellar filament, the centreline rfib(s) of the fibres, parametrised by6the contour length position s, is described mathematically asrfib(s) = ( Rfl cos ( sRfl/ sinα) , hRfl sin ( sRfl/ sinα) , s cosα ) , −LLfib < s < LRfib, (1)with total contour length Lfib = L L fib + L R fib, where the authors allow for fibres extending to both sides of the base of the tail to have lengths LLfib (left side) and L R fib (right side).
Here again, the crucial factor −hRflωfl sinα cosα appears in both equations multiplying a positive, non-dimensional expression, and the authors obtain the correct directionality and speed of translocation in agreement with Ref. [27].
These mathematical results capture the basic qualitative experimental observations and predictions of Refs. [23, 27] for the speed and directionality of translocation which are both crucial for successful infection.
The factor −hωfl gives a directionality for U in agreement with the qualitative prediction of Ref. [27] that CCW rotation will only pull the phage toward the cell body if the phage slides along a right-handed groove.
These results are valid in the limit in which the distance d between the fibre and the surface of the flagellar filaments is much smaller than the radius of the flagellar filament (d Rfl), such that the surface of the smooth flagellar filament is locally planar.
The long-tailed approximation from Eq. 63, through the terms with Lt in both numerator and denominator, is able to capture the increasing behaviour of U with Lt. Physically, this trend is caused by the propulsive terms in ez ·Mtail in Eq. 40 (proportional to L3t ) that increase as Lt increases.
17The important point where the two models deviate from each other is their opposite predictions for the translocation speed as a function of the phage tail length and the phage fibre length.
there will be an additional hydrodynamic drag on the phage due to the rotation and translation of the flagellar filament.