PHYSICAL REVIEW C 81, 024304 (2010)
Image reconstruction techniques applied to nuclear mass models
Irving O. Morales,
1
P. Van Isacker,
2
V. Velazquez,
3
J. Barea,
4
J. Mendoza-Temis,
1
J. C. L
´
opez Vieyra,
1
J. G. Hirsch,
1
and A. Frank
1
1
Instituto de Ciencias Nucleares, Universidad Nacional Aut
´
onoma de M
´
exico, 04510 M
´
exico, D.F., Mexico
2
Grand Acc
´
el
´
erateur National d’Ions Lourds, CEA/DSM–CNRS/IN2P3, Bo
ˆ
ıte Postale 55027, F-14076 Caen Cedex 5, France
3
Facultad de Ciencias, Universidad Nacional Aut
´
onoma de M
´
exico, 04510 M
´
exico, D.F., Mexico
4
Instituto de Estructura de la Materia, Consejo Superior de Investigaciones Cient
´
ıficas, Unidad Asociada al Departamento de F
´
ısica
At
´
omica, Molecular y Nuclear, Facultad de F
´
ısica, Universidad de Sevilla, Apartado 1065, E-41080 Sevilla, Spain
(Received 14 April 2009; revised manuscript received 11 January 2010; published 5 February 2010)
A new procedure is presented that combines well-known nuclear models with image reconstruction techniques.
A color-coded image is built by taking the differences between measured masses and the predictions given by the
different theoretical models. This image is viewed as part of a larger array in the (N,Z) plane, where unknown
nuclear masses are hidden, covered by a “mask.” We apply a suitably adapted deconvolution algorithm, used in
astronomical observations, to “open the window” and see the rest of the pattern. We show that it is possible to
improve significantly mass predictions in regions not too far from measured nuclear masses.
DOI: 10.1103/PhysRevC.81.024304 PACS number(s): 21.10.Dr, 42.30.Wb
I. INTRODUCTION
Nuclei are particularly complex systems, ranging from
a single proton to more than three hundred nucleons; too
large for a detailed microscopic treatment but too small for
statistical methods. Interest in them is not restricted to nuclear
physicists because the atomic nuclei that constitute our world
are manufactured inside stars, defining their evolution and fate.
Arguably, the most basic property of a nucleus is its mass.
Understanding nuclear masses provides a test of our basic
knowledge of nuclear structure and is an essential ingredient
of the fundamental astrophysical problem of nucleosynthesis,
which often takes place in far-from-stability conditions, on
ultrashort time scales [1]. Though great progress has been
made in measuring the mass of short-lived nuclei that are far
from the region of stable, naturally occurring isotopes, theory
is needed to predict their properties and guide experiments
that search, for example, for regions of increased stability [2].
Despite the efforts invested in developing techniques that can
accurately describe these masses, the predictions made by
different models often turn out to be disconcertingly different,
even in regions close to known masses. Reliable theoretical
models and methodologies that can predict the mass and other
properties of these “exotic” nuclei are still missing [3].
The efforts to calculate nuclear masses have been hampered
by the absence of a true effective theory of the nuclear
interaction and by the difficulties inherent to quantum many-
body calculations. Instead, simplified approaches to model the
atomic nucleus have been devised. The cornerstone of nuclear
mass models is the semi-empirical mass formula proposed by
von Weizs
¨
acker [4] and Bethe and Bacher [5] in the 1930s,
which is based on a picture of the nucleus as a uniform,
very dense, charged liquid drop—the so-called liquid-drop
model (LDM)—which gives an accurate overall description of
nuclear masses, but lacks some quantum-mechanical effects
due to shell closures, pairing, quadrupole correlations, etc.
Thus, large deviations from the measured masses are observed
in certain regions of the nuclear chart. The inclusion of these
effects usually requires other treatments, like the finite-range
droplet model [6], which combines macroscopic effects with
microscopic shell and pairing corrections, the model of Duflo
and Zuker [7], and the Hartree-Fock approach [8]. In general,
however, it is difficult to match theory and experiment (for
all known nuclei) with an average precision better than about
0.5 MeV [3]. More troublesome is the fact that different model
predictions tend to diverge from each other for regions of nuclei
with unknown mass.
II. SYSTEMATIC PATTERNS
The starting point in the proposed approach is the striking
color patterns in the (N,Z) plane shown in Fig. 1, which result
after taking the difference between the experimentally known
masses [9] and predictions of several models: an improved
macroscopic LDM [10], an upgrade of the LDM by the inclu-
sion of schematic microscopic shell corrections [10] (LDMM),
the 31-parameter Duflo-Zuker (DZ) model [7], and the Garvey-
Kelson (GK) relations [11]. For each model, we observe a
residual systematic pattern related to the physics and that is not
included in the model. Thus, for example, the LDM does not
contain microscopic information on independent-particle mo-
tion, and consequently the pattern shows systematic deviations
related to shell closures, nuclear deformations, and residual
interactions in a compelling graphic form [see Fig. 1(a)].
The microscopic behavior can be parametrized by the inclusion
of a schematic microscopic shell correction [10]:
BE
LDMM
(N,Z) ≡ BE
LDM
(N,Z)
− a
f
F
max
+ a
ff
FF
max
+ a
const
, (1)
where BE
LDM
is the nuclear binding energy as obtained in the
LDM and
F
max
=
n
ν
+ n
π
2
−
n
ν
+ n
π
2
,
FF
max
=
n
ν
+ n
π
2
2
−
n
ν
+ n
π
2
2
,
0556-2813/2010/81(2)/024304(9) 024304-1 ©2010 The American Physical Society

IRVING O. MORALES et al. PHYSICAL REVIEW C 81, 024304 (2010)
FIG. 1. (Color online) Differences between experimental masses and those calculated with the four models: (a) the liquid-drop model
(LDM), (b) the liquid-drop model with schematic shell correction (LDMM), (c) the Duflo-Zuker model (DZ), and (d) the Garvey-Kelson
relations (GK).
are linear and quadratic terms in the numbers of valence
neutron n
ν
(proton n
π
) particles or holes, counted from
the nearest closed shell, and the quantities in brackets are
their average values. The constant a
const
, used to re-center
the prediction average (see Ref. [10]), and a
f
and a
ff
are
parameters found by fitting the experimental masses. Although
this parametrization still leads to large errors, it is able to
schematically reproduce the main trends observed in the mass
surface near the shell closures. These terms are similar to
the ones used in parametrizations proposed by R. F. Casten
[12]. The inclusion of these terms reduces the rms deviation
but some systematic patterns still appear, as is shown in
Fig. 1(b) (note the change of scale). Finally, if we take
a more complex approach such as the DZ model, we still
observe small but systematically correlated errors [Fig. 1(c)].
The remaining patterns suggest physics that have not been
incorporated into the models. Figure 1(d) displays the differ-
ence between experimental masses and masses obtained from
the GK relations [11]. The remaining deviations are, in this
case, close to white noise, which shows that it is in principle
possible to predict masses to a significantly better precision
and, therefore, that it is worthwhile to attempt to take into
account the missing physical effects (see, however, Ref. [13]).
III. IMAGE RECONSTRUCTION
The patterns shown in Fig. 1 suggest an approach to mass
prediction based on image reconstruction techniques. The
basic idea is to consider that the more than 2000 differences
between the different models and the known nuclear masses
represent partial views of a larger image array in the (N,Z)
plane, and that all other mass differences (perhaps around 7000
in number) that exist between the neutron and proton drip lines
remain hidden, covered by a “mask.” Thus, the question is
whether we can “open the window” to unveil the remaining
pattern, or at least part of it. We show here that indeed this
information can be reliably uncovered, at least for regions
not too far from measured masses, with image reconstruction
techniques. The success of the approach strongly depends upon
whether the physical features associated with the changing
patterns in the nuclear landscape can be coded in terms of
(global) regularities in the (N,Z) plane, and whether they
can in turn be modeled by a finite number of harmonic
components. An important assumption in this approach is
that the observed regularity and relative smoothness of the
mass-difference landscape remains throughout [14]. Although
substantial changes in mass differences may occur in a
rather short interval (e.g., because of shell structure or shape
transitions), there are no sudden jumps from one nucleus to
another. Figure 1(a) shows that, to a good approximation, the
landscape can be considered to vary smoothly as a function
of nucleon number. More precise checks of this assumption
can be made, for example by testing whether the GK relations
(which are a measure of smoothness) become increasingly
inaccurate for predictions further away from stable nuclei.
Our tests indicate that this is not the case—they remain equally
accurate, even when approaching areas close to the drip lines
[15]. We are thus motivated to follow this approach further.
024304-2

IMAGE RECONSTRUCTION TECHNIQUES APPLIED TO ... PHYSICAL REVIEW C 81, 024304 (2010)
We display the mass-difference table by a two-dimensional
array of pixels, with N in the horizontal position and Z in
the vertical one. Differences between experimental masses
m
expt
(N,Z) and calculated masses m
th
(N,Z) define the color
image function
i(N,Z) ≡ m
th
(N,Z) − m
expt
(N,Z). (2)
The relationship between i(N,Z) and the full pattern m(N,Z)
is then given by
i(N,Z) = m(N,Z) · w(N,Z), (3)
where w(N,Z) is a binary mask function, taking the value 1
for positions (N,Z) where nuclear masses are known, and 0
otherwise (although a “weighted” mask may be used instead—
see Ref. [16]). We thus need to extract m(N,Z) from Eq. (3).
If I (k
N
,k
Z
), M(k
N
,k
Z
), and W (k
N
,k
Z
) are the Fourier
transforms of i(N,Z), m(N,Z), and w(N,Z), respectively,
then
I (k
N
,k
Z
) = M(k
N
,k
Z
) ∗ W (k
N
,K
Z
), (4)
where M ∗ W is the convolution of the functions M and W .
Since both i(N,Z) and w(N,Z) are known for the entire
domain, their Fourier transforms I (k
N
,k
Z
) and W (k
N
,k
Z
)
can be evaluated directly. The problem is narrowed down
to obtaining the function M(k
N
,k
Z
), from which m(N,Z)
can be recovered by applying an inverse Fourier transform.
Formally, this is a deconvolution problem. Deconvolution is
nontrivial and may lead to non-unique solutions, but there exist
several algorithms, such as the CLEAN method, often used in
radio astronomy [17], and the maximum entropy method [18],
which provide testable methodologies. We have chosen a
specially adapted version of the CLEAN algorithm used in
the reconstruction of texture patches [19].
The main assumption of the CLEAN method is that the
remaining patterns shown in Fig. 1 can be modeled by a finite
number of harmonic components. The Fourier spectrum of
the known data I (k
N
,k
Z
) is viewed as a corrupt version of
the Fourier spectrum of the complete data M (k
N
,k
Z
). This
corruption is due to the mask and the main goal is to remove
this noise and construct a clean Fourier spectrum, choosing
those components that best explain the observed patterns in
the image.
The uncorrupted version of the spectrum is made of
components such as
T (k
N
,k
Z
) = aδ(k
N
− u, k
Z
− v) + a
∗
δ(k
N
+ u, k
Z
+ v),
(5)
where a is the complex amplitude of the component and (u, v)
is the position in Fourier space. The effect of the mask on this
component is
I (k
N
,k
Z
) = T (k
N
,k
Z
) ∗ W (k
N
,K
Z
), (6)
and by expanding the convolution we obtain
I (k
N
,k
Z
) = aW(k
N
− u, k
Z
− v) + a
∗
W (k
N
+ u, k
Z
+ v),
(7)
so that this single component becomes distorted. The form
of the mask guarantees that the dominant peak of its Fourier
spectrum is the DC or constant term (u, v = 0) and, because
of this, the position remains unaltered, only the amplitude
is changed due to the mask, and the corruption of the mask
appears as additional smaller peaks around the component.
To achieve the deconvolution it is necessary to determine the
nature of the original component, namely the true amplitude
and position (a, u, v) given the corrupted Fourier spectrum
I (k
N
,k
Z
) and the Fourier spectrum of the mask M(k
N
,k
Z
).
Because the position of the true components remains the
same and the spurious peaks are smaller than the principal
ones, we can find the principal component of the data by
locating the major pair in I (k
N
,k
Z
). Substitution of k
N
= u
and k
Z
= v in Eq. (7)gives
I (u, v) = aW(0, 0) + a
∗
W (2u, 2v), (8)
which we can rearrange using the conjugate into
a =
I (u, v)W (0, 0) − I
∗
(u, v)W (2u, 2v)
W (0, 0)
2
− W (2u, 2v)W
∗
(2u, 2v)
. (9)
Thus, we can recover the true amplitude of the original
harmonic component T (k
N
,k
Z
) and the true nature of
the component is thus obtained for both the position and
amplitude.
The CLEAN algorithm essentially proceeds by sequentially
finding the frequency position of the peak with maximal
intensity in the corrupted Fourier spectrum. Once this peak
is located, the true amplitude is calculated with Eq. (9) and a
clean version of the Fourier spectrum is updated. This clean
spectrum is constructed placing the component in the true
frequency and with the correct amplitude before proceeding to
the next iteration. A new version of the corrupted spectrum is
calculated eliminating the removed component and the effects
produced on it by the mask. The new corrupted spectrum is
called the residual spectrum.
If R
i
(k
N
,k
Z
)istheith residual and R
0
(k
N
,k
Z
) =
I (k
N
,k
Z
), the CLEAN algorithm consists of the following
steps:
(i) Locate the position (u
i
,v
i
)oftheith clean component
from the maximum of R
i−1
(k
N
,k
Z
).
(ii) Calculate the true amplitude with Eq. (9).
(iii) Generate the ith residual spectrum
R
i
(k
N
,k
Z
) = R
i−1
(k
N
,k
Z
)
− (a
i
W (k
N
− u
i
,k
Z
− v
i
)
+ a
∗
W (k
N
+ u
i
,k
Z
+ v
i
)). (10)
This procedure is repeated until a stopping criterion is reached
at iteration K, after which the clean spectrum C(k
N
,k
Z
)is
constructed:
C(k
N
,k
Z
) =
K
i=1
(a
i
δ(k
N
− u
i
,k
Z
− v
i
)
+ a
i∗
δ(k
N
+ u
i
,k
Z
+ v
i
)). (11)
Once the clean spectrum is constructed, the concealed image
is obtained by applying the inverse Fourier transform to it.
024304-3

IRVING O. MORALES et al. PHYSICAL REVIEW C 81, 024304 (2010)
IV. MASS PREDICTIONS
With the algorithm described previously it is possible
to extrapolate the remaining patterns shown by the mass
differences m = m
expt
− m
th
. Once this extrapolated pattern
is obtained, it is then possible to predict the nuclear masses by
adding the mass predicted by the model:
m(N,Z) = m
extrapolated
(N,Z) + m
th
(N,Z). (12)
It is in this sense that the CLEAN algorithm is able to improve
on the model used to calculate the mass differences.
In order to provide a measure of the degree of improvement
of the model used for the mass differences, two tests have
been applied. In the first we take the set of measured masses
with N 28,Z 28 from the Atomic Mass Evaluation 2003
(AME03) compilation of Audi et al. [9] and divide it into
two subsets. We use the 1454 masses present in the previous
AME95 compilation [20] as input to generate the pattern (by
fitting the mass model’s parameters using this set), and then
we measure the predictability of the model by calculating mass
differences for the other 371 experimental masses [21]. These
predictions can subsequently be compared with the results
obtained by applying CLEAN to the same input subset, as we
explain below. We refer to this as the “AME95-03 test.” This
test has been extensively used before to measure the predictive
power of nuclear mass models [3]. The second test consists
of predicting the mass differences of 301 nuclei at the border
of the AME03-measured landscape [21], following the same
procedure as in the first test. We have applied both tests to
three models with different degrees of accuracy. The first is
a macroscopic LDM with 7 parameters (Eq. (2) in Ref. [10])
that are determined by fitting (a) the (updated) AME95 data for
the AME95-03 test, or (b) the AME03 data without the border
for the AME03-border test. The second model is an upgraded
version of this macroscopic LDM, denoted by LDMM, and
described in Sec. II. Finally, the third mass model used for the
reconstruction is the 31-parameter DZ model [7].
In these tests the CLEAN method is iterated until a rms
deviation of 100 keV is achieved for the input data fit. Table I
shows a comparison of the rms deviations for the AME95-03
test, and those obtained with the CLEAN method for each
model. Table II gives a similar comparison for the AME03-
border test.
In the AME95-03 test the largest CLEAN improvement
(∼62% rms reduction) is obtained for the LDMM of Eq. (1).
The improved rms, surprisingly, is comparable with the
corresponding rms in the DZ model (see Table I). For the
simple LDM (Eq. (2) in Ref. [10]) we also find a large rms
reduction of ∼54%, whereas for the DZ model we find it
TABLE I. AME95-03 test: Predictability for the set
of nuclei in AME03 but not in AME95, restricted to
N,Z 28.
Model RMS RMS (with CLEAN)
LDM, Eq. (2)in[10] 1.9307 MeV 0.8763 MeV
LDMM, Eq. (1) 0.9955 MeV 0.3718 MeV
DZ model [7] 0.3348 MeV 0.2727 MeV
TABLE II. AME03-border test: Predictability for the
set of nuclei in the border of AME03, restricted to
N,Z 28.
Model RMS RMS (with CLEAN)
LDM, Eq. (2)in[10] 2.7763 MeV 0.9168 MeV
LDMM, Eq. (1) 1.9804 MeV 0.9333 MeV
DZ model [7] 0.4039 MeV 0.3133 MeV
to be ∼20%. The latter, smaller improvement is expected,
because this model is already in very good agreement with
the experimental masses. Nevertheless, this rms reduction
represents a significant correction.
A similar situation occurs for the AME03-border test. The
largest improvement (∼66% rms reduction) occurs for the
macroscopic LDM, followed by LDMM of Eq. (1) with a
∼52% rms reduction. Again, as in the AME95-03 test, the
rms in the DZ model decreases by ∼20%. These results
suggest that the CLEAN method can efficiently incorporate
the residual patterns observed in the experimental masses. The
rms, however, being an average measure, is not a sufficiently
clear gauge. Therefore, we now turn to an amplified view of
our results, using two-neutron separation energies S
2n
.
Two-neutron separation energies, S
2n
(N,Z) ≡ BE(N,
Z) − BE(N − 2,Z), contain detailed information about nu-
clear structure effects. In Figs. 2, 3, and 4 we plot S
2n
for
isotope series in the N ∼ 78–128 region for the AME95-03
test using the LDM, the LDMM of Eq. (1), and the DZ model,
respectively.
The predictions of the macroscopic LDM, as shown in
Fig. 2, are completely flat, with no structure at all. In contrast,
the data display strong variations at the magic numbers N = 82
and 126, and substructures near N ∼ 90. After reconstruction,
those structures are well described (with an rms of ∼0.1MeV)
in the fitted region (AME95 data). On the other hand, the
benchmark AME03 data are also surprisingly well predicted
(with an rms of 0.8763 MeV—see Table I). Although the
shell structures are well described by the CLEAN algorithm,
the reconstruction is not sufficiently constrained. This is
illustrated by the presence of spurious substructures that,
although small in magnitude, are not seen in the S
2n
data.
To minimize such spurious effects, it is necessary to impose
additional constraints, and this can be achieved, for example,
by schematically including shell correction terms as is done in
the LDMM of Eq. (1).
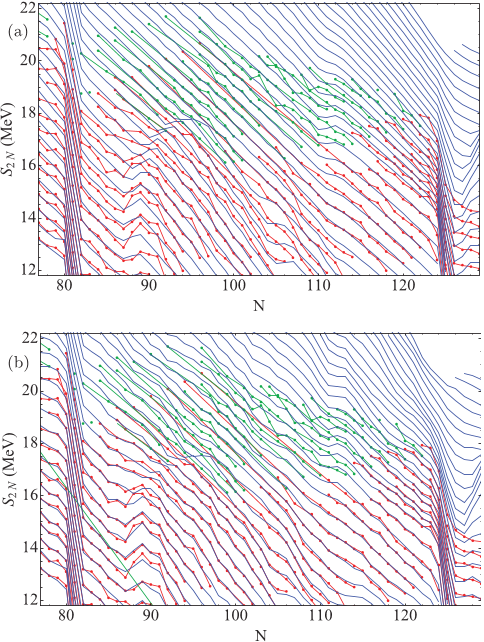
Figure 3 shows S
2n
in the N ∼ 78–128 region of the
AME95-03 test, obtained with the LDMM [isotopic lines
in Fig. 3(a)], and the results obtained after applying the
reconstruction algorithm [isotopic lines in Fig. 3(b)]. In the
LDMM, the magic numbers N = 82 and 126 are incorporated
into the model from the beginning. The experimental S
2n
in
those regions displays discontinuities that are well described
by the LDMM. However, the substructure observed in the
data at N ∼ 90 is not properly accounted for [see Fig. 3(a)].
After applying the reconstruction to LDMM, the substructure
is correctly described (with an rms of ∼0.1 MeV) in the fitted
region. It is remarkable that the region of the benchmark
AME03 data (green bullets in Fig. 3) is also accurately
024304-4

IMAGE RECONSTRUCTION TECHNIQUES APPLIED TO ... PHYSICAL REVIEW C 81, 024304 (2010)
80 90 100 110 120
12
14
16
18
20
22
N
S
2
N
MeV
(a)
80 90 100 110 120
12
14
16
18
20
22
N
S
2 N
MeV
(b)
FIG. 2. (Color online) AME95-03 test: Two-neutron separation
energies S
2n
isotopic lines (in blue) predicted by (a) the LDM
and (b) its improvement using the CLEAN reconstruction. Red
bullets indicate the input (fitted) data and green bullets indicate the
benchmark (predicted) data.
predicted (with an rms of 0.3718 MeV—see Table I). The
constraints imposed by the schematic shell-correction terms
in the LDMM of Eq. (1) are thus sufficient to remove the
spurious substructure observed in the LDM reconstruction.
The results for S
2n
obtained with the DZ model in the N ∼
78–128 region of the AME95-03 test, and its improvement by
the image reconstruction method, are shown in Figs. 4(a) and
4(b), respectively. In this case, the DZ model shows the pres-
ence of the substructure at N ∼ 90, but the experimental S
2n
are not accurately described. Furthermore, the isotopic lines
become flat outside the region where measurements are avail-
able. The DZ model has an rms of 0.3384 MeV (see Table I),
giving an excellent overall description of S
2n
in the predicted
region. Nevertheless, the reconstruction method can be used
to improve the description by a significant ∼20%.
Figures 2, 3, and 4 show that the main effect of applying
the CLEAN algorithm to the predictions of the various models
is to add “texture” to the mass surface, which corresponds to
some of the physical effects not included in the model.
We have made similar tests in the N ∼ 110–160 region for
the AME03-border case, using the S
2n
obtained with the LDM,
LDMM, and DZ models, and the corresponding calculations
using the image reconstruction method. The improvements as
a result of the CLEAN procedure are of the same quality as
for the AME95-03 test.
80 90 100 110 120
12
14
16
18
20
22
S
2 N
(MeV)
80 90 100 110 120
12
14
16
18
20
22
N
N
S
2 N
(MeV)
(a)
(b)
FIG. 3. (Color online) AME95-03 test: Two-neutron separation
energies S
2n
isotopic lines (in blue) predicted by (a) the LDMM
and (b) its improvement using the CLEAN reconstruction. Red
bullets indicate the input (fitted) data and green bullets indicate the
benchmark (predicted) data.
The mass predictions obtained applying the CLEAN
algorithm to the DZ model are comparable to the best
available global mass predictions. However, it is of interest
to also compare them with the masses recommended by
Audi et al. [20], which are predicted using the systematic
trends of the mass surface and its derivatives. This method
provides the best short-range mass extrapolations [3], which
have been published for sets of three or four nuclides in the
neighborhood of those with measured masses in the Atomic
Mass Evaluations [9,20]. These predictions are performed
nucleus by nucleus, combining a (rather elaborate) graphical
analysis with relevant physical information [9]. This procedure
leads to an rms of 0.1615 MeV for the predictions corre-
sponding to the AME95-03 test. Since these extrapolations are
more accurate than the DZ+CLEAN predictions, we expect
that the masses obtained applying the CLEAN algorithm to
the DZ model should be closer to the predictions of Audi
et al. than the DZ masses. In order to test this we have
calculated the rms deviation between the masses extrapolated
by Audi et al. and the predictions of the DZ model with and
without CLEAN. For the DZ model we obtain an rms of
0.3305 MeV while for the DZ+CLEAN predictions we get
an rms of 0.2694 MeV, which is significantly smaller. This
shows that the DZ predictions are indeed improved using the
CLEAN algorithm.
024304-5