Open Research Online
The Open University’s repository of research publications
and other research outputs
Increase in |S
L
| induced by channel coupling: the case
of deuteron scattering
Journal Item
How to cite:
Mackintosh, R.S. and Pang, D.Y. (2012). Increase in |SL| induced by channel coupling: the case of deuteron
scattering. Physical Review C, 86(4) 047602.
For guidance on citations see FAQs.
c
2012 American Physical Society
Version: Version of Record
Link(s) to article on publisher’s website:
http://dx.doi.org/doi:10.1103/PhysRevC.86.047602
http://prc.aps.org/abstract/PRC/v86/i4/e047602
Copyright and Moral Rights for the articles on this site are retained by the individual authors and/or other copyright
owners. For more information on Open Research Online’s data policy on reuse of materials please consult the p olicies
page.
oro.open.ac.uk

PHYSICAL REVIEW C 86, 047602 (2012)
Increase in |S
L
| induced by channel coupling: The case of deuteron breakup
R. S. Mackintosh
*
Department of Physical Sciences, The Open University, Milton Keynes, MK7 6AA, United Kingdom
D. Y. Pang
†
School of Physics and Nuclear Energy Engineering, Beihang University, Beijing, 100191, China
(Received 26 July 2012; published 9 October 2012)
For deuteron scattering from
58
Ni at laboratory energies of 56, 79, and 120 MeV, we study the dynamic
polarization potentials (DPPs) induced by S-wave and D-wave breakup (BU), separately and together, in order to
gain insight into the nature of the DPP as well as a counterintuitive property: the existence of L values for which
the BU coupling increases |S
L
|, a ‘wrong-way’ effect. The effect is associated with the existence of emissive
regions in the imaginary DPP, suggesting a connection with the nonlocal nature of the DPP. T he same relationship
was previously found for
6
Li scattering, indicating a generic effect bearing on the dynamics of nuclear reactions.
DOI: 10.1103/PhysRevC.86.047602 PACS number(s): 25.45.De, 24.50.+g, 24.10.Ht, 24.10.Eq
I. INTRODUCTION
Reference [1] presented a study of the dynamic polarization
potential (DPP) due to projectile breakup for
6
Li nuclei
scattering from
12
C at energies from 90 to 318 MeV. At the
lower energies, and for certain values of partial-wave angular
momentum L, the magnitude |S
L
| of the elastic channel S ma-
trix went the ‘wrong way’ (WW) when coupling to t he breakup
channels was switched on, i.e., |S
L
| increased. For these
values of L, channel coupling reduced the absorption from the
elastic channel. There appeared to be an association between
this occurrence and the appearance of generative (emissive)
regions in the local equivalent dynamic polarization potential.
This WW phenomenon was noted long ago [2] and occurs in
other scattering cases, for example,
6
He scattering at energies
near the barrier [3–5]. In that case, too, emissive regions appear
in the imaginary part of the DPP due to breakup (BU). Not all
cases of channel coupling result in a WW effect. For example,
the reaction channel coupling of protons to deuteron channels
modifies the proton elastic |S
lj
| the ‘right way.’ There appears
to be a correlation: with p ↔ d (no WW), the change in total
cross section in the elastic channel due to the coupling far ex-
ceeds the cross section to the deuteron reaction channels; how-
ever, with BU of
6
Li [ 1], the reverse is the case and the BU cross
section is greater than the increase in total reaction cross sec-
tion that occurs with BU coupling. In the case of p ↔ d cou-
pling, the other correlate with WW, noted above, the presence
of emissive regions in the DPP, occurs only slightly in the sur-
face region; see Ref. [6]. The WW phenomenon appears to be
one effect of the nonlocality of the DPP. In line with Austern’s
discussion [7], the coupling removes flux from the interaction
region returning (some of it) elsewhere in the nucleus.
This work is not a comprehensive study of the effect of
coupled channels on deuteron scattering; that would require
the inclusion of (d ↔ p) and (d ↔ t ) couplings and many
*
r.mackintosh@open.ac.uk
†
dypang@buaa.edu.cn
other processes. It is also not a comprehensive study of the
effect of projectile breakup on deuteron scattering; that would
require a more complete description of the deuteron and its
breakup. It is a study, based mainly on deuteron breakup, of
an anomalous generic feature of scattering that seems to be
related to nonlocal effects of channel coupling.
II. CDCC CALCULATIONS
Continuum discretized coupled channels (CDCC) calcula-
tions were carried out, with the standard formalism using the
code
FRESCO [8], in order to study the contribution of deuteron
breakup (BU) to the effective deuteron-nucleus interaction.
Calculations included coupling to the S-wave continuum
(SBU), the D-wave continuum (DBU), and both continua
(SDBU) since we had observed different degrees of WW
for the SBU and SDBU cases. The deuteron was described
as an S-wave state in a Gaussian potential: V (r) = 72.15 ×
exp [−(r/1.484)
2
] MeV. Nuclear and Coulomb breakup were
included and the maximum multipole order in the expansion of
the coupling potentials was q = 4. The continuum discretiza-
tion was specified by k
max
= 1.0fm
−1
, with k = 0.05 fm
−1
,
i.e., continuum energies up to 42 MeV.
Proton-target and neutron-target potentials were
determined by renormalizing the potentials of the Bruy
`
eres
Jeukenne-Lejeune-Mahaux (JLMB) folding model [9]. The
measured experimental data were fitted in a grid search
by the elastic scattering angular distributions for SDBU
calculations. The elastic scattering angular distributions for
SBU and DBU calculations will not be fitted, but the DPPs
will not depend strongly upon these potentials. Fitting the
angular distributions for SDBU calculations was a suitable
compromise context for studying the DPPs for all cases. In
the SDBU case there is full coupling between the states i n the
S-wave and D-wave continua.
The JLMB normalization factors for each energy presented
in Table I are quite close to unity. The last two columns of
this table give the volume integrals of the resulting deuteron-
nucleus folded potential, the ‘bare potential’ for that energy.
Subtracting this from the potentials found by inverting the
047602-1
0556-2813/2012/86(4)/047602(5) ©2012 American Physical Society

BRIEF REPORTS PHYSICAL REVIEW C 86, 047602 (2012)
TABLE I. Real and imaginary renormalization factors N
R
and
N
I
for the p-
58
Ni and n-
58
Ni potentials. The last two columns give
volume integrals of the real and imaginary components of the folded
d-
58
Ni potential in MeV fm
3
.
E
lab
N
R
N
I
J
R
J
I
56.0 0.90 1.05 341.25 102.18
79.0 0.95 1.05 330.33 106.30
120.0 0.95 1.05 280.88 108.49
elastic channel S-matrix from the CDCC calculations yields
the DPPs presented below. The maximum radius for the CCDC
calculations was 60 fm with a step size of 0.05 fm, satisfactory
for elastic scattering. The Coulomb radius was 1.25 × 58
1/3
fm. No spin-orbit interactions were included. The fits to the
angular distributions are presented in Fig. 1.
III. THE ANOMALOUS BEHAVIOR OF |S
L
| FOR
DEUTERON SCATTERING
Figure 2 shows three representative cases of the effect of
breakup coupling on the magnitude |S
L
| of the elastic channel
S matrix. In Fig. 2(a) for 56 MeV and S-wave breakup, the
coupling increases |S
L
| over two partial waves, L = 11 and
L = 12. In Fig. 2(b) for 79 MeV and D-wave breakup, |S
L
| is
slightly increased for just one L.InFig.2(c) for 120 MeV and
both S- and D-wave breakup, there is no increase in |S
L
| for any
L. These three cases are referred to in Table II, discussed below,
as showing WW, only just showing WW, and not showing WW.
For the 56 MeV cases not shown, both DBU and SDBU cases
show WW for one L value rather than the two for SBU.
IV. CALCULATION OF DPP
For each energy, the bare potential is subtracted from the
potential found by inverting [10,11] the elastic channel S
10
-3
10
-2
10
-1
10
0
10
1
10
2
0 20 40 60 80 100 120 140 160
σ/σ
Ruth
θ
c.m.
(deg)
56 MeV (x100)
79 MeV
120 MeV (x0.01)
exp
no coupling
SBU
DBU
SDBU
FIG. 1. For 56, 79, and 120 MeV deuterons on
56
Ni, the fit to
the experimental angular distributions (large dots) with no coupling
(double dotted line), S-wave breakup (dots), D-wave breakup (small
dashes), and the full CDCC calculation with S-wave and D-wave
breakup (solid line).
0.0
0.3
0.6
0.9
56 MeV
(a)
SBU
no couplings
0.0
0.2
10 11 12 13
0.0
0.3
0.6
0.9
|S
L
|
79 MeV
(b)
DBU
0.1
0.2
0.3
11 12 13 14
0.0
0.3
0.6
0.9
5 10 15 20 25
L
120 MeV
(c)
SDBU
FIG. 2. For deuterons on
56
Ni, the magnitude of the elastic scat-
tering matrix, |S
L
|. The dashed lines are for no coupling to breakup
channels and the solid lines are for coupling included as follows:
(a) 56 MeV, S-wave breakup, (b) 79 MeV, D-wave breakup, and
(c) 120 MeV, S-andD-wave breakup.
matrix, S
L
, from the CDCC calculations. The difference is the
DPP (actually, the local equivalent of the formal nonlocal and
L-dependent DPP) arising from the breakup coupling for that
energy. The characteristics of the resulting DPPs are presented
in Table II: the volume integrals, J
R
and J
I
, of the real and
imaginary parts of the DPPs are calculated by subtracting the
corresponding volume integral of the bare potential from that
of the inverted potential. We also present the differences in
the rms radii, R
R
and R
I
, due to breakup coupling, σ
reac
,
the change in total reaction cross section induced by breakup,
and the cross section, CDCC σ
BU
, into the particular breakup
channels that were included. The SBU column presents the
results for the case with S-wave breakup channels only, the
DBU column is for D-wave breakup, and the SDBU column
is for both S-wave and D-wave continua included and coupled
together. The last column presents the numerical sums of
the quantities for S-wave breakup and D-wave breakup for
comparison with SDBU values. The sum has some significance
for J
R
and J
I
, but we include the sums for R
R
and
R
I
as well, and comment on the results. The line labeled
‘Emissive’ indicates whether there is an emissive region in
the imaginary part of the DPP around 4 fm, as will be seen
in figures presented below. All potentials exhibit an emissive
region near the nuclear center. The last line indicates whether
there are partial waves for which |S
l
| goes the wrong way
(WW), i.e., increases, when the indicated coupling is included.
From Table II we note a link between WW and an emissive
region in the DPP. The WW effect appears to be strongest at
lower energies, and is inhibited by D-wave BU.
In the SDBU column of Table II, the line CDCC σ
BU
presents the separate SBU and DBU cross sections to both
the S-wave BU channels and D-wave BU channels and their
sum, the total BU cross section. The individual values are
much less than for the SBU and DBU calculations.
The following cases have a cross section to the BU channels
that exceeds the increase in total cross section induced by
047602-2

BRIEF REPORTS PHYSICAL REVIEW C 86, 047602 (2012)
TABLE II. For deuteron scattering from
58
Ni, volume integrals J (in MeV fm
3
) of the real and i maginary DPPs induced by projectile
breakup. Convention used: Positive is attractive or absorptive.
Quantity SBU DBU SDBU SBU + DBU
56 MeV
J
R
4.77 −6.24 −1.55 − 1.47
J
I
15.25 15.06 18.29 30.31
R
R
−0.042 −0.0628 −0.141 − 0.1048
R
I
0.0643 0.2245 0.1956 0.2888
σ
reac
90.4 86.6 86.7 177.0
CDCC σ
BU
84.65 88.25 83.62 = 32.31 + 51.31 172.90
Emissive ? yes yes yes
WW ? yes yes yes
79 MeV
J
R
3.67 −4.65 −0.85 − 0.98
J
I
13.19 12.36 17.11 25.55
R
R
−0.0406 −0.0659 −0.135 − 0.1065
R
I
0.0390 0.2066 0.1649 0.2465
σ
reac
76.7 86.2 93.40 162.9
CDCC σ
BU
75.35 93.76 97.36 = 32.07 + 65.29 169.11
Emissive ? yes yes yes, small
WW ? yes yes, just no
120 MeV
J
R
1.90 −2.55 −0.72 − 0.65
J
I
9.59 7.66 13.57 17.25
R
R
−0.0346 −0.0634 −0.1165 − 0.0980
R
I
0.0080 0.1415 0.0983 0.1395
σ
reac
49.4 63.2 76.1 112.6
CDCC σ
BU
52.17 75.86 90.12 = 27.17 + 62.41 128.03
Emissive ? yes yes no
WW ? yes, weak no no
the BU coupling: DBU at 56 MeV; DBU and SDBU at
79 MeV; SBU, DBU, and SDBU at 120 MeV. This suggests
the suppression of fusion by breakup, a well-known effect at
lower energies.
The sums in the last column of Table II agree quite well for
the real, but not imaginary, DPPs. The J
R
values agree even
though they are small in magnitude as a result of subtraction
between substantial surface repulsion and interior attractive
effects. We show below that in the asymptotic radial range
(7 fm and beyond), the SBU and DBU real DPPs add quite
closely to the SDBU real DPP. In Ref. [12] and references
therein, the lack of additivity of DPPs for channels that are
not mutually coupled provided evidence for the nonlocality
of the underlying DPP, but in the present case it was not
possible to switch off the coupling between the S-wave and
D-wave continua. Thus it is the near additivity of J
R
, not the
nonadditivity of J
I
, that is noteworthy. The sum of the SBU
and DBU breakup cross sections greatly exceeds the SDBU
breakup cross section, in line with the nonadditivity of J
I
.
The radial forms of the real and imaginary parts of the DPPs
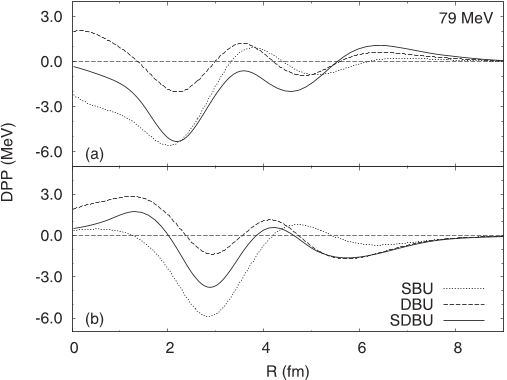
are presented for 56, 79, and 120 MeV in Figs. 3–5. The DPPs
behave in a very regular way, falling somewhat in magnitude
with increasing energy. Concerning the real DPP, we note
that for SBU it is mostly attractive, with only weak surface
repulsion, whereas for DBU it is much more repulsive in the
surface. The SDBU DPP shows clear surface repulsion and
interior attraction. The repulsive-tending bump at all energies
near 3.5 fm almost makes the DPP repulsive at 56 MeV. The
total (bare plus DPP) real potential is attractive for all r but its
rms radius is reduced at all energies.
The overall shape of the imaginary DPP varies regularly
with energy. The absorption has a maximum magnitude in the
-6.0
-3.0
0.0
3.0
56 MeV
(a)
-6.0
-3.0
0.0
3.0
0 2 4 6 8
DPP (MeV)
R (fm)
(b)
SBU
DBU
SDBU
FIG. 3. For 56 MeV deuterons on
56
Ni, (a) the real and (b) the
imaginary components of the DPP generated by S-wave breakup
(dots), D-wave breakup (short dashes), and for S-wave and D-wave
breakup included together (solid line).
047602-3

BRIEF REPORTS PHYSICAL REVIEW C 86, 047602 (2012)
-6.0
-3.0
0.0
3.0
79 MeV
(a)
-6.0
-3.0
0.0
3.0
0 2 4 6 8
DPP (MeV)
R (fm)
(b)
SBU
DBU
SDBU
FIG. 4. For 79 MeV deuterons on
56
Ni, as for Fig. 3.
surface around 6 fm, which is greatest at low energies. There
is an emissive peak at the nuclear center at all energies. More
significant is the bump at around 4 fm that becomes emissive at
79 MeV and especially at 56 MeV. We postulate a connection
between this emissiveness and the tendency for a WW effect
that is most pronounced at the lowest energy. The systematic
features of the DPP are consistent with the generic properties
presented long ago [13].
Is the emissivity near 4 fm, apparently associated with
WW, of empirical significance? In the case of
6
Li [1], a notch
test showed that the emissive region in the DPP was within
the radial range that could be sensitive to elastic scattering.
Deuteron scattering is much more sensitive to the nuclear
interior; see, e.g. the model-independent fitting of Ermer
et al. [14]. Their model-independent potential for 52 MeV
deuterons scattering from
40
Ca revealed emissive regions in
the full potential, not just DPPs. The present work makes that
more plausible. It might be interesting to modify the central
potential to remove the emissive feature near r = 0, examine
its effect on the angular distribution, and verify that it is not
associated with the WW effect.
V. GENERIC EFFECT: COMPARISON WITH
6
Li ON
12
C
The above calculations were prompted by the results of
Ref. [1] where a relationship between WW effects and emissive
regions appeared in the DPP due to breakup of
6
Li on
12
C.
-6.0
-3.0
0.0
3.0
120 MeV
(a)
-6.0
-3.0
0.0
3.0
0 2 4 6 8
DPP (MeV)
R (fm)
(b)
SBU
DBU
SDBU
FIG. 5. For 120 MeV deuterons on
56
Ni, as for Fig. 3.
Figure 9 of that paper shows the trend of how |S
L
| is modified
by BU of
6
Li for five energies from 90 to 380 MeV. We
restate here the key facts: At 90 MeV, WW occurs for L = 12
(slightly), L = 13 (|S
L
| almost doubled), and L = 14 (|S
L
|
increased by about 70%) and the imaginary DPP becomes
emissive by almost 3 MeV between 2 and 3 fm. At 123.5 MeV,
|S
L
| has a bump at L = 11 but just misses going WW, while
the DPP has an emissive peak with a maximum value of about
2 MeV. At 168.6 MeV there is neither WW nor an emissive
region. Finally, we note that the extent to which the BU cross
section exceeds the increase in reaction cross section due to
breakup falls with energy, the ratio being 2.91 at 90 MeV, 2.35
at 123.5 MeV, and 2.18 at 168.6 MeV. There appears to be a
generic effect of projectile breakup.
We intend to carry out ψ-potential studies [15,16]ofthese
and similar cases to investigate the spatial distribution of
absorption and emission within the target nucleus. This might
throw light on the causation of WW and its relationship to
Austern’s account [7] of nonlocality in nuclear interactions, a
fundamental aspect nuclear interaction dynamics. We note a
contemporary requirement [17] for a precise understanding of
deuteron reactions.
ACKNOWLEDGMENT
This work is supported by the the National Natural Science
Foundation of China (Nos. 11035001 and 11275018).
[1] D. Y. Pang and R. S. Mackintosh, Phys.Rev.C84, 064611
(2011).
[2] R. S. Mackintosh and A. A. Ioannides, in Advanced Methods
in the Evaluation of Nuclear Scattering Data, Lecture Notes in
Physics 236 (Springer-Verlag, Berlin, 1985), p. 283.
[3] R. S. Mackintosh and N. Keeley, Phys.Rev.C70, 024604
(2004).
[4] R.S.MackintoshandN.Keeley,Phys.Rev.C79, 014611 (2009).
[5] N. Keeley, R. S. Mackintosh, and C. Beck, Nucl. Phys. A 834,
792c (2010).
[6] R. S. Mackintosh and N. Keeley, Phys.Rev.C85, 064603
(2012).
[7] N. Austern, Phys.Rev.B137, 752 (1965).
[8] I. J. Thompson, Comput. Phys. Rep. 7, 167 (1988).
[9] E. Bauge, J. P. Delaroche, and M. Girod, Phys.Rev.C63, 024607
(2001).
047602-4