




Did you find this useful? Give us your feedback









186 citations
55 citations
54 citations
...Forsgren, Gill and Griffin [10] extend constraint-based preconditioners to deal with regularized saddle point systems using an approximation of the (1, 1) block coupled with an augmenting term (related to a product with the constraint matrix and regularized (2, 2) block)....
[...]
48 citations
48 citations
2,277 citations
...The main focus ∗Received by the editors January 17, 2006; accepted for publication (in revised form) March 5, 2007; published electronically August 22, 2007....
[...]
2,253 citations
...This paper concerns the formulation and analysis of preconditioned iterative methods for the solution of augmented systems of the form (1.1) ( H −AT A G )( x1 x2 ) = ( b1 b2 ) , with A an m×n matrix, H symmetric, and G symmetric positive semidefinite....
[...]
2,205 citations
1,644 citations
1,551 citations
zero elements of G are associated with linearized equality constraints, where the corresponding subset of equations (5.1) are the Newton equations for a zero of the constraint residual.
The interior-point method requires the solution of systems with a KKT matrix of the form(6.1)( H −JT−J −Γ) ,where H is the n × n Hessian of the Lagrangian, J is the m × n Jacobian matrix of constraint gradients, and Γ is a positive-definite diagonal with some large and smallCopyright © by SIAM.
If the zero elements of G are associated with linear constraints, and the system (5.3) is solved exactly, it suffices to compute the special step y only once, when solving the first system.
The authors prefer to do the analysis in terms of the doubly augmented system because it provides the parameterization based on the scalar parameter ν.Copyright © by SIAM.
provided that the constraint preconditioner is applied exactly at every PCG step, the right-hand side of (5.3) will remain zero for all subsequent iterations.
It should be emphasized that the choice of C and B affects only the efficiency of the active-set constraint preconditioners and not the definition of the linear equations that need to be solved.
An advantage of using preconditioning in conjunction with the doubly augmented system is that the linear equations used to apply the preconditioner need not be solved exactly.
The preconditioner (4.5) has the factorization P 1P(ν) = RPP 2 P(ν)R T P , where RPis the upper-triangular matrix (4.2a) and P 2P(ν) is given by(4.6) P 2P(ν) = ⎛⎝M + (1 + ν)ATCD−1C AC νATCνAC νDC νDB ⎞⎠ .
In this strict-complementarity case, the authors expect that the proposed preconditioners would asymptotically give a cluster of 700 unit eigenvalues.
Consider the PCG method applied to a generic symmetric system Ax = b with symmetric positive-definite preconditioner P and initial iterate x0 = 0.
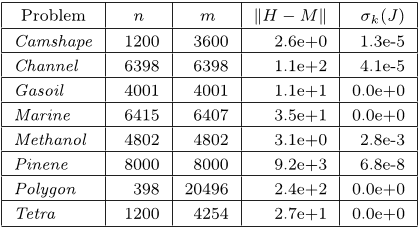
The data for the test matrices was generated using a primaldual trust-region method (see, e.g., [16, 20, 32]) applied to eight problems, Camshape, Channel, Gasoil, Marine, Methanol, Pinene, Polygon, and Tetra, from the COPS 3.0 test collection [6, 8, 9, 10].
Theorems 3.6 and 4.1 predict that for the preconditioners P (1) and P 1P(1), 700 (= m + rank(AS)) eigenvalues of the preconditioned matrix will cluster close to unity, with 600 of these eigenvalues exactly equal to one.
Since SC is independent of ν, the spectrum of P 1P(ν)−1B(ν) is also independent of ν. Lemma 3.5 implies that SC has at least rank(AS) eigenvalues that are 1 + O ( μ1/2 ) , which establishes part (b).To establish part (c), the authors need to estimate the difference between the eigenvalues of SC and S, where S is given by (3.3a).
For their example with 100 variables and 100,000 inequality constraints, a matrix of dimension 150 would need to be factored instead of a matrix of dimension 100,100.
Without loss of generality it may be assumed that the rows of A are ordered so that the m1 row indices in S corresponding to linearlyCopyright © by SIAM.