



Did you find this useful? Give us your feedback















31 citations
7 citations
5 citations
3 citations
...[23] apply Kalman gain to minimise target error and Zhang, Ji...
[...]
...Similar to the approach mentioned in [23] we use Kalman Gain to minimize the error between the estimated and actual measurements....
[...]
...as mentioned in [23] is used to minimize the error between the estimated and actual values by the tracker module....
[...]
2 citations
...In [10], an efficient SMC–PHD filter based on the Kalman–gain approach was proposed to...
[...]
7 citations
...Additionally, there are other works in the literature that combine the implementation of the GM and particle PHD filter into one filter such as the GM particle PHD filter in [27] and [29] and the Gaussian mixture SMC-PHD in [30]....
[...]
5 citations
...2) Extended Particle Filter (EPF): Given that the measurement model of (4) is nonlinear, but Gaussian, it is possible to use a proposal distribution that exploits a linear approximation to the posterior [19] in the same way as the extended Kalman filter (EKF) uses a local linearization about its estimates....
[...]
...As an attempt to solve the importance sampling problem, Maskell and Julier [19] proposed an optimized proposal distribution for SMC filters with multiple modes in general....
[...]
...These errors arise due to the stochastic nature of drawing samples from the proposal distribution and the stochasticity of the resampling process [19]....
[...]
...Furthermore, in MTT which involves multiple modalities, if particles are in clusters representing the modes of the posterior, the iterative process of randomly drawing samples from proposal distributions results in random fluctuations in the total weight attributed to each mode [19]....
[...]
...h(fk−1(xk−1)) is then evaluated at each sigma point and Hk computed from these samples [19]....
[...]
5 citations
...[25] proposed the Kalman particle PHD filter for multitarget visual tracking, which uses the Kalman filter to construct the proposal density also in the prediction step....
[...]
4 citations
2 citations
...[26] presented an improvement to the SMC-PHD filter, which incorporates the latest measurements into the resampling step by using the UKF....
[...]
In their future work, the proposed filter will be extended to track maneuvering and closely spaced targets and applied to other target tracking applications including that in a multipleinput-multiple-output ( MIMO ) radar environment.
In the AP-PHD filter implementation, 1000 particles were used per existing track and 10005 particles were used for the newborn track.
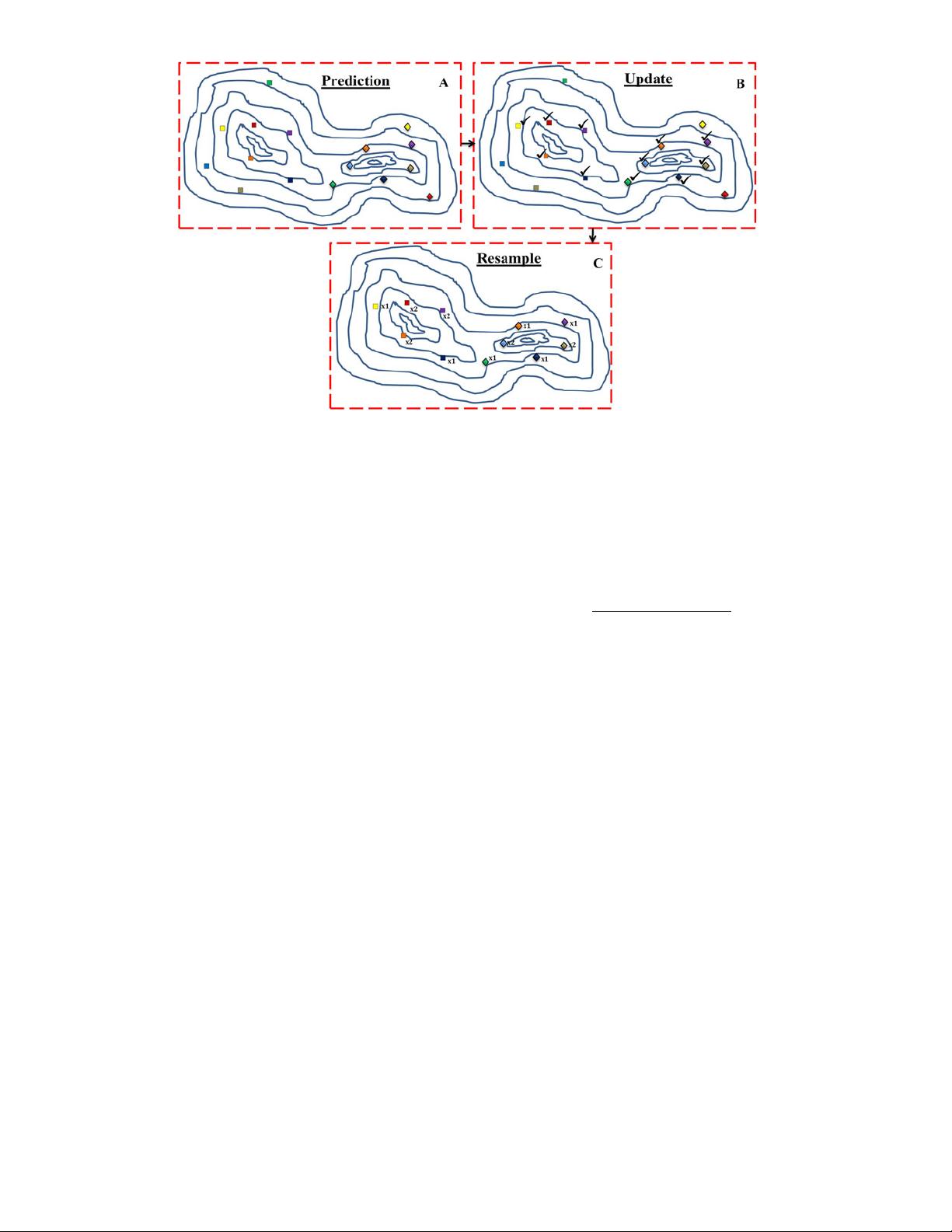
the Kalman gain as a correction technique seeks to achieve minimal variance and thereby gives better accuracy (in approximating the posterior).
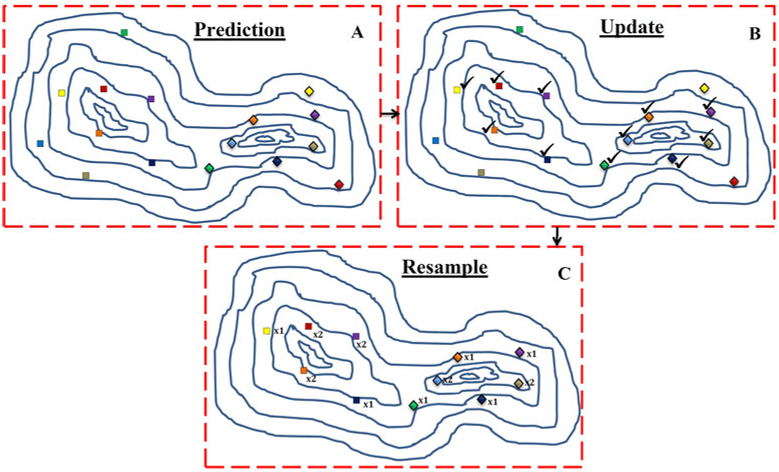
The auxiliary importance sampling [23] process starts with the selection of the measurements that are well described by the targets states extracted from the estimated PHD and this is achieved using the auction algorithm.
In their future work, the proposed filter will be extended to track maneuvering and closely spaced targets and applied to other target tracking applications including that in a multipleinput-multiple-output (MIMO) radar environment.
Tables V and VI show filter performance results averaged over 1000 MC runs with and without measurement set partition, respectively.
The t th target-originated nonlinear measurement model is given aszk = hk(xk, nk) (4) where hk(·) is a nonlinear function and nk is an i.i.d. process noise vector.
the above measurement set partition approach can be applied under the following assumptions: that newborn targets exist for at least two consecutive time steps, the maneuvering of targets is not too abrupt, the sample period δt is not too large, measurement noise is not too large, clutter is not too dense, and clutter is not time correlated.
The maximum number of Guassian terms was set to 100, with the merging (Tm) and pruning threshold (Tp) set at 10 m and 10−3, respectively.
The plots indicate that the proposed filter with ρ = 500 particles per existing track is able to properly track all targets and in addition to being able to identify all target births and deaths while successfully accommodating nonlinearities under high clutter condition.
The tracking performance was improved because only target-originated measurements were used for weight computation and the MSE at each time step was reduced resulting in fewer number of particles for state estimation.
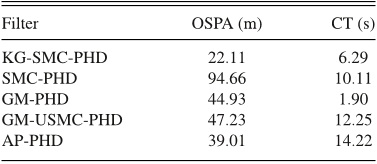
Fig. 7 clearly shows that the proposed filter outperforms the SMC-PHD filter as it maintains an average OSPA distance of less than 51 m up to clutter intensity of κk = 8 × 10−3 (radm)−1 due to the particle state correction technique in their approach while the SMC-PHD filter starts to exhibit breakdown from about κk = 6.4 × 10−3 (radm)−1 (i.e., λ = 40).
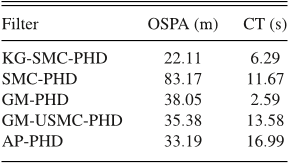
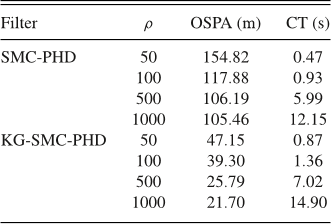
in Table V, it can be observed that with just 500 particles per existing track, the KG-SMCPHD filter outperformed all other filters by having lower OSPA distance.
The authors now discuss the filter limitations in terms of OSPA distance and number of clutter points, number of particles and CT as well as general filter performance.
In terms of miss-distance, Fig. 8 also suggests that the proposed filter is more efficient as only few a particles (less than 1000) are required to achieve an OSPA distance of less than 50 m while the SMC-PHD filter requires about 10 000 particles.
respectively, asx̃lk|k−1 ≈ { qk(·|x̃lk−1, Żk), l = 1, . . . , Lk−1 pk(·|Żk), l = Lk−1 + 1, . . . ,Lk (30)with corresponding weightsw̃lk|k−1 =⎧ ⎪⎪⎪⎨⎪⎪⎪⎩φk|k−1(x̃lk, x̃ l k−1)qk(x̃k|k−1|x̃lk−1,Zk) wlk−1, l = 1, . . . , Lk−1γk(x̃lk) Jkpk(x̃k|k−1|Zk) , l=Lk−1 +1, . . . ,Lk(31) with the termφk|k−1(xk, xk−1) = pS(xk−1)fk|k−1(xk, xk−1) + bk|k−1(xk, xk−1)where Lk = Lk−1 + Jk , qk(·|·) and pk(·|·) denote the proposal distributions for persistent and newborn targets, respectively; γk(·) is the PHD of the spontaneous birth, pS(·) is the probability of target survival, fk|k−1(xk, xk−1) is the single target motion model, and bk|k−1(xk, xk−1) is the PHD of spawned targets;
This is because both EPF and UPF helps us to place generated samples “under” measurements as soon as measurements become available.