
Local Commuting Projector Hamiltonians and
the Quantum Hall Effect
Anton Kapustin
California Institute of Technology, Pasadena, California
Lukasz Fidkowski
Department of Physics, University of Washington, Seattle
October 22, 2018
Abstract
We prove that neither Integer nor Fractional Quantum Hall Ef-
fects with nonzero Hall conductivity are possible in gapped systems
described by Local Commuting Projector Hamiltonians.
1
arXiv:1810.07756v1 [cond-mat.str-el] 17 Oct 2018

1 Introduction
One of the simplest classes of exactly soluble many-body Hamiltoni-
ans is the class of Local Commuting Projector Hamiltonians (LCPH).
These are finite-range lattice Hamiltonians which have the form
H =
X
Γ
Φ(Γ),
where the local terms Φ(Γ) are commuting projectors. Usually one
also assumes that each local Hilbert space is finite-dimensional, oth-
erwise one gets a hugely degenerate excitation spectrum. The toric
code [1], or more generally, Levin-Wen Hamiltonians associated to
unitary spherical fusion categories [2], provide interesting examples
of such Hamiltonians in two dimensions, so many topologically or-
dered states can be described by LCPH. It is believed that all known
Symmetry Protected Topological phases of fermions and bosons with
a finite symmetry can also be described by LCPH. Nevertheless, it
is also widely believed that neither IQHE nor FQHE phases can be
realized by LCPH. In this short note, we provide a proof of this.
More precisely, we prove the following. Suppose H is a local lat-
tice Hamiltonian with an on-site U(1) symmetry defined on a torus
of size L. It is well-known that it is possible to extend H to a 2-
parameter family H(β
x
, β
y
) of local lattice Hamiltonians depending
on the “holonomies”
1
(β
x
, β
y
) ∈ R
2
/(2πZ)
2
. If H(β
x
, β
y
) has a unique
ground state for all β
x
, β
y
, then its ground-states form a rank-one vec-
tor bundle E over T
β
= R
2
/(2πZ)
2
. It was argued in [3, 4] that the
first Chern number of E is equal to the Hall conductance of the system.
More precisely, the Hall conductance is defined in the thermodynamic
limit L → ∞. If one assumes that the limiting ground state exists, and
the spectral gap does not close in the limit L → ∞, one can indeed
prove that the thermodynamic limit of the first Chern number of E
exists and is equal to the Hall conductance [5, 6, 7]. (There is an al-
ternative proof of the quantization of the Hall conductance which only
requires H to be gapped, but does not make any assumption about
the gap for nonzero β
x
, β
y
[8]). This line of reasoning extends to the
case when the ground-state is degenerate [6]: if the thermodynamic
limit of all ground-states is the same, then the limit of the first Chern
1
In many papers “holonomies” are called fluxes. We find this terminology confusing,
since the word “flux” is also used to describe a region of nonzero magnetic field, while
β
x
, β
y
parameterize a flat U(1) gauge field on a torus.
2

number exists and is equal to q times the Hall conductance, where q
is the degeneracy of the ground-states on a torus of a sufficiently large
size. We prove the following
Theorem. Let H be an LCPH with range R on a torus of size
L > 4R, and suppose H has an on-site U(1) symmetry. Then the 2-
parameter family H(β
x
, β
y
) of Hamiltonians depending on the ”holonomies”
β
x
, β
y
∈ R
2
/(2πZ)
2
is a family of LCPH, and thus the gap assumption
is satisfied. Moreover, the Chern number of the corresponding bundle
of ground-states vanishes.
Assuming that the thermodynamic limit exists, this implies that
neither IQHE nor FQHE states can be realized by Local Commuting
Projector Hamiltonians with an on-site U(1) symmetry.
While for simplicity we only discuss the case d = 2, in arbitrary
dimension the same arguments show that all Chern classes of the bun-
dle of ground-states vanish if H is an LCPH, and in fact the bundle
of ground-states is topologically trivial.
The proof uses some well-known results from algebraic geometry.
The same mathematical results were used in [11] to show that a Chern
insulator with a finite-range band Hamiltonian cannot have correla-
tions which decay faster than any exponential. This is no coincidence:
correlations of all local observables in a ground-state of an LCPH van-
ish beyond a finite range. One might conjecture that neither IQHE
nor FQHE can occur if correlations of all local observables decay faster
than any exponential.
The content of the paper is as follows. In section 2, we recall the
definition of a local lattice Hamiltonian on a torus with holonomies
following [8, 6]. The proof of the theorem occupies sections 3 and 4.
The work was partly performed at the Aspen Center for Physics,
which is supported by National Science Foundation grant PHY-1607611.
The research of A. K. was supported by the U.S. Department of En-
ergy, Office of Science, Office of High Energy Physics, under Award
Number de-sc0011632 and by the Simons Investigator Award. L. F.
was supported by NSF DMR-1519579
2 Lattice Hamiltonian on a torus with
holonomies
The space will be a torus T
2
of size L × L. We identify it with
R
2
/(LZ)
2
. A lattice is a finite subset Λ ⊂ T
2
. The Hilbert space
3

is either a tensor product
V = ⊗
λ∈Λ
V
λ
,
where V
λ
is a finite-dimensional Hilbert space, or a super-tensor prod-
uct
V =
b
⊗
λ∈Λ
V
λ
,
where V
λ
is a finite-dimensional Z
2
-graded Hilbert space. We will
denote by A
Γ
the algebra of observables supported at a subset Γ ∈ Λ.
Following [8], we use an `
1
distance on T
2
:
dist(p, p
0
) = |x(p) − x(p
0
)|modL + |y(p) − y(p
0
)|modL.
A local lattice Hamiltonian with range R has the form
H =
X
Γ
Φ(Γ),
where Φ(Γ) is a Hermitian element of A
Γ
, and the sum is over all
subsets Γ ⊂ Λ of diameter less than R. In the Z
2
-graded case, each
Φ(Γ) is required to be even. In addition, one usually assumes that the
norms of the operators Φ(Γ) are uniformly bounded [8]. In the cases
of interest to us, this will be automatic.
A local lattice Hamiltonian is said to have an on-site symmetry G
if each V
λ
is a unitary (or anti-unitary) representation of G, and each
Φ(Γ) commutes with the action of G on A
Γ
. In particular, a local
lattice Hamiltonian has an on-site symmetry U(1) if for each λ ∈ Λ
we are given an (even) Hermitian operator Q
λ
: V
λ
→ V
λ
with integral
eigenvalues, and for all Γ of diameter less than R we have
[Φ(Γ), Q(Γ)] = 0,
where
Q(Γ) =
X
λ∈Γ
Q
λ
.
Note that Q(Γ) is additive under disjoint union:
Q(Γ ∪ Γ
0
) = Q(Γ) + Q(Γ
0
), if Γ ∩ Γ
0
= ∅.
Given a local lattice Hamiltonian with an on-site U(1) symmetry
and range R, and assuming L > 2R, one can define a family of local
lattice Hamiltonians with range R depending on (β
x
, β
y
) ∈ R
2
/(2πZ)
2
4
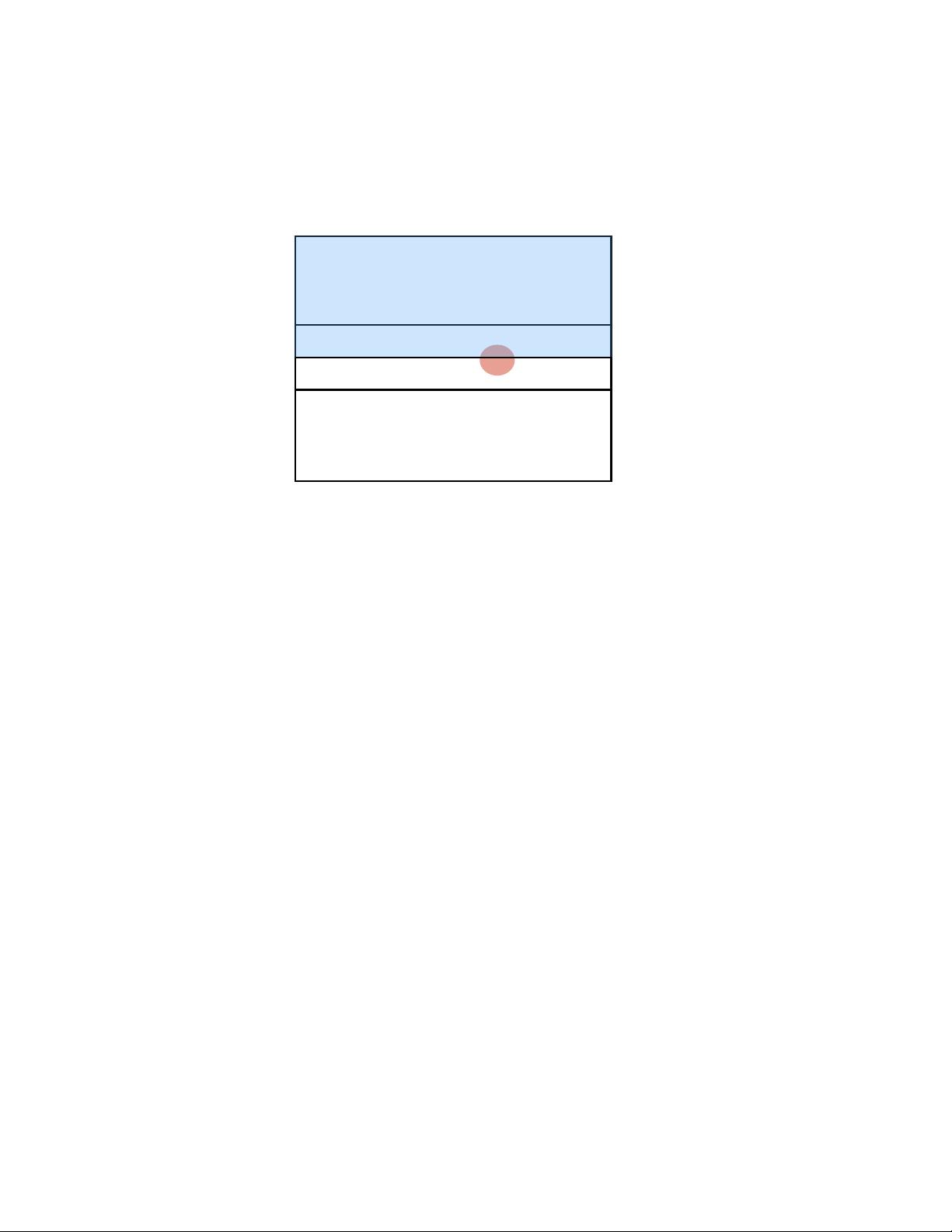
y=R
y=L-R
T
d
y=0
y=L/2
Figure 1: The operator Φ(Γ, 0, β
y
) is equal to Φ(Γ) unless Φ(Γ) straddles the
line y = 0 (red region), in which case it is defined by e
−iβ
y
Q(Λ
d
)
Φ(Γ)e
iβ
y
Q(Λ
d
)
,
where Q(Λ
d
) is the operator that measures the U(1) charge of T
d
(blue re-
gion).
as follows [8, 6, 7]. Let T
`
be the subset of T
2
given by 0 < x(p) < L/2.
Let T
d
be the subset of T
2
given by 0 < y < L/2. Let Λ
`
= Λ
T
T
`
and Λ
d
= Λ
T
T
d
. We define (see Fig. 1)
Φ(Γ, 0, β
y
) =
e
−iβ
y
Q(Λ
d
)
Φ(Γ)e
iβ
y
Q(Λ
d
)
if Γ
T
Λ
d
6= ∅, dist(Γ, {y = 0}) < R,
Φ(Γ) otherwise
Then we define
Φ(Γ, β
x
, β
y
) =
e
−iβ
x
Q(Λ
`
)
Φ(Γ, 0, β
y
)e
iβ
x
Q(Λ
`
)
if Γ
T
Λ
`
6= ∅, dist(Γ, {x = 0}) < R,
Φ(Γ, 0, β
y
) otherwise
It follows from U(1)-invariance of Φ(Γ) and additivity of Q(Γ) that
Φ(Γ, β
x
, β
y
) is an element of A
Γ
, and thus
H(β
x
, β
y
) =
X
Γ
Φ(Γ, β
x
, β
y
)
is a local lattice Hamiltonian. Since Q
λ
has integral eigenvalues, it is
clear that each Φ(Γ, β
x
, β
y
) is 2π-periodic in both β
x
and β
y
. Thus
H(β
x
, β
y
) is a family of local lattice Hamiltonians parameterized by
points of a torus T
β
= R
2
/(2πZ)
2
.
5
