




read more









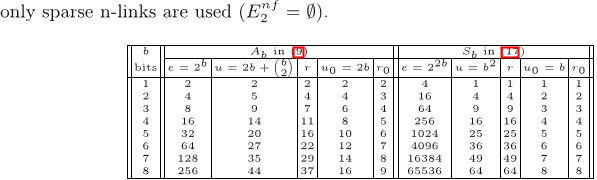
More elaborate analysis of the algorithm ( e. g. error bounds, value of the minimized energy, computational complexity, running times ) and comparison with state-of-the-art approaches on standard benchmarks is left for future work.
The LS error in edge weights induces error in the s − t cut or binary labeling, which is decoded into a suboptimal solution to the multi-label problem.
Many visual computing tasks can be formulated as graph labeling problems, e.g. segmentation and stereo-reconstruction [1], in which one out of k labels is assigned to each graph vertex.
The authors perform a single (non-iterative and initialization-independent) s − t cut to obtain a “Gray” binary encoding, which is then unambiguously decoded into the k labels.
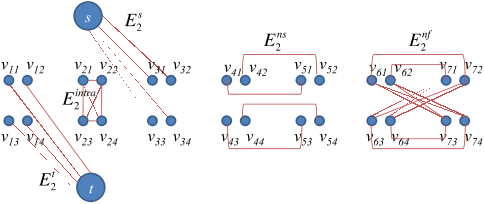
the cost of severing intra-links in G2 to assign li to vertex vi in G isDintrai (li) =b∑m=1b∑n=m+1(lim ⊕ lin) wvim,vin (3)where ⊕ denotes binary XOR.
every sequence of b binary labels (vij)bj=1 is decoded to a decimal label li ∈ Lk = {l0, l1, ..., lk−1}, ∀vi ∈ V , i.e. the solution to the original multi-label MRF problem.
The authors then construct GLSE , a noisy version of G, by adding uniformly distributed noise with support [0, noise level] to the edge weights.
the authors are exploring the use of non-negative least squares (e.g. Chapter 23 in [16]) to guarantee non-negative edge weights as well as quantifying the benefits of the Gray encoding.
The Markov random field (MRF) formulation captures this desired label interaction via an energy ξ(l) to be minimized with respect to the vertex labels l.ξ(l) = ∑vi∈V Di(li) + λ∑(vi,vj)∈E Vij(li, lj , di, dj) (1)where Di(li) penalizes labeling vi with li, and Vij , aka prior, penalizes assigning labels (li, lj) to neighboring vertices1.
If Vij(li, lj , di, dj) = Vij(di, dj), i.e. label-independent, the authors can simply ignore the outcome of li ⊕ lj by setting it to a constant.
The calculated edge weights are optimal in the sense that they minimize the least squares (LS) error when solving a linear system of equations capturing the original MRF penalties.
(4)The interaction penalty Vij(li, lj, di, dj) for assigning li to vi and lj to neighboring vj in G must equal the cost of assigning a sequence of binary labels (lim)bm=1 to (vim)bm=1 and (ljn) b n=1 to (vin) b n=1 in G2.
the cost of severing t-links in G2 to assign li to vertex vi in G is calculated asDtlinksi (li) =b∑j=1lijwvij ,s + l̄ijwvij ,t (2)where l̄ij denotes the unary complement (NOT) of lij .
For b = 2, (5) simplifies toVij(li, lj , di, dj) = (li1 ⊕ lj1)wvi1,vj1 + (li1 ⊕ lj2)wvi1,vj2+ (li2 ⊕ lj1)wvi2,vj1 + (li2 ⊕ lj2)wvi2,vj2 (15)The authors can now substitute all possible 2b2b = 22b = 16 combinations of the pairs of interacting labels (li, lj)∈{l0, l1, l2, l3}×{l0, l1, l2, l3}, or equivalently, ((li)2, (lj)2) ∈ {00, 01, 10, 11}× {00, 01, 10, 11}.
in the general case when Vij depends on the labels li and lj of the neighboring vertices vi and vj , a single edge weight is insufficient to capture such elaborate label interactions, intuitively, because wi,j needs to take on a different value for every pair of labels.