Parsimonious hydrological modeling of urban sewer and river catchments

TL;DR: In this paper, a parsimonious model of flow capable of simulating flow in natural/engineered catchments and at WWTP (Wastewater Treatment Plant) inlets was developed.

About: This article is published in Journal of Hydrology.The article was published on 2012-09-25 and is currently open access. It has received 36 citations till now. The article focuses on the topics: Impervious surface & Combined sewer.

Summary

1. Introduction

• Catchment modeling is a mature discipline, and much research and modeling has been carried out on natural catchments.
• Such models are valuable for many purposes, of course.
• Aquatic Science and Technolerland. , Swiss Federal Institute of m/, last accessed December and Woolhiser (2002) for a review).
• The model integrates the main physical processes in urban catchments (i.e., precipitation, infiltration, soil moisture, runoff, streamflow and groundwater flow), but without consideration of the detailed pipe drainage network.
• In urban systems, these two endpoints drain overlapping basins.

2. Design and mathematical description of the model

• The basin is modeled as a set of three storages (one surface and two subsurface), each characterized by a state variable representing the water stored within it (Fig. 1).
• The two meteorological forcings considered are precipitation and air temperature, T, both assumed uniform over the basin.
• The subterranean layer is represented as composed of two reservoirs: the upper soil (or root zone) region and the groundwater region with, respectively, storages of Su and Sg (Botter et al., 2010).

2.1. Modeling of surface processes

• This water bypasses the subsurface flow, and is treated as a separate component in the lumped model.
• When falling on the pervious fraction of the basin, the rain can either infiltrate or produce overland flow.
• This storage also receives the precipitation flux falling on any impervious surfaces, jAi.
• The output, Q sup, from this storage produces the fast component of the total streamflow.

2.2. Modeling of subsurface processes

• Surface infiltration enters the root zone storage, the total volume of which is: Su ¼ ZhAp; ð3Þ with Z [L] the depth of the active soil layer.
• Two types of outputs from this region are considered: evapotranspiration, ET, and deep percolation, Je.

ET ¼ ApETmaxf ðhÞ; ð4Þ

• A fraction jAi of the rainfall enters this apotranspires or percolates to the subsurface linear reservoir (Sg ).
• Note that same ulate flow at the WWTP entrance, the subsurface reservoir discharges into the pipe to artificial inputs from water use (see Section 2.4).
• The maximum evapotranspiration is computed through a modified version of the Blaney–Criddle equation (e.g., Doorenbos and Pruitt, 1975): ETmax ¼ aþ b½pð0:46Tþ 8:13Þ ; ð6Þ where a and b are fitting parameters and p is the mean annual percentage of daytime hours, which varies only with latitude (Allen et al., 1998).
• This formulation of subterranean flow, based on Botter et al. (2010), is easily extendible to account for interflow (or subsurface runoff) through shallow soil layers.

2.3. Consideration of CSOs

• A characteristic feature of hybrid sewer networks are CSOs.
• In the drainage network, CSOs divert flows above a certain level directly to receiving waters, rather than to the WWTP (Butler and Davies, 2010; Lee and Bang, 2000; Wisner et al., 1981).
• The authors consider in this study that a single, representative flow delimiter is sufficient to model the effect of all CSOs of the system in a lumped fashion manner.
• This representative CSO is modeled using a diversion law that follows a linear threshold-limited function (in Fig. 2).

2.4. Dynamics of wastewater production

• During dry weather, discharges arriving at the WWTP inlet are determined mainly by two phenomena: (i) infiltration of groundwater into the pipe network (see Section 2.2 and Dupont et al. (2006); Göbel et al. (2004)) and, (ii) water use and consequent wastewater production.
• This ‘artificial’ water input, which is not present in a natural catchment, is modeled based on statistical analysis presented by Jordan (2010).
• Monthly, daily and hourly flow coefficients are extrapolated from temporal series analysis and considered as characteristic of the system.
• This includes direct water consumption in households, and all parasitic clear water (fountains, street washing, industrial uses, etc).

3. Optimization of hydrological quality index

• Model calibration was performed based on the two objective functions in Table 1, since this combination has been found to yield better overall fits (Hingray et al., 2009; Perrin et al., 2001).
• The list of fitting criteria and the range of prior values given before calibration process can be found in Table 2.
• Similarly to Fenicia et al. (2006) and Seibert (2000), the calibration approach adopted here is based on a Monte Carlo algorithm designed to optimize the model performance, using the Nash–Sutcliffe (NS) and the Normalized Bias (NB) criteria (Table 1).
• The former places an emphasis on the model’s ability to estimate large magnitudes (i.e., peak discharge), while the latter weights more the deviation between simulated and observed water balance, as follows: Minfð1 NSÞþ j NB jg: ð10Þ 4 http://www.meteosuisse.ch, last accessed January 2012.

4.1. Application of the model to an urban basin: Modeling of flow at the river outlet and WWTP entrance

• The same modeling framework is employed to model both the dynamics of flows at an urban river outlet and inlet of a local WWTP.
• The application area is the city of Lausanne in Switzerland, which has a population of about 200,000 and is characterized by a steep average gradient towards nearby Lake Geneva.
• A feature of Lausanne is that the WWTP catchment and the river catchment overlap over a fraction of the city (Fig. 3).
• The model is calibrated twice on the same time period, once to model the WWTP input, and once to model the river output to the adjacent Lake Geneva, which is the receiving water body for both river and WWTP discharges.

4.2. Application to the WWTP basin

• The WWTP catchment under study is the Lausanne hybrid (partially-separate) sewer system, drains to the Vidy Bay WWTP.
• A large part of the water is in consequence diverted through drainage out of the WWTP basin.
• The flow rate at the WWTP entrance during significant storm events is attenuated by the presence of CSOs; this behavior is captured by the simulator.
• The modeling results in Fig. 4 do not capture perfectly the measured data.

4.3. Application to the river basin

• The modeled river, called the Vuachère, is located in the eastern part of the city of Lausanne (Fig. 3).
• The flow rate was measured at the outlet of the river basin, just before discharge into Lake Geneva.
• The calibration and validation periods were taken the same as for the WWTP basin modeling.
• Different factors in the model drive the simulated flow dynamics in the river.

5. Sensitivity analysis

• A sensitivity analysis was conducted to estimate the influence of the model parameters (Table 2).
• Each parameter was varied within the prior range of acceptable values for this parameter, and the two fitting criteria (Nash–Sutcliff and Normal Bias) computed.
• The authors see from Fig. 7 that two parameters mainly govern the overall performance of the model.
• These are the discharge constants of the surface impervious reservoir (ksup) and the subsurface reservoir (ksub).
• On the other hand, changes in the ksub value degrade the ability of the model to reproduce the base flow, and thus move the Normal Bias criterion away from its optimal value of 0, in addition to affecting the Nash–Sutcliff criterion.

6. Discussion

• The lumped modeling approach was designed to predict, with an identical framework, both flow at the WWTP inlet and at the outlet of the river basin overlapping the WWTP catchment.
• Saturation excess could be easily implemented but at cost of additional calibration parameter.
• Another key assumption is the way CSOs are represented.
• For the river, CSOs provide additional water as excess water in the pipe network is diverted to prevent overloading the WWTP.
• In agreement with Leon et al. (2010), the study presented here presents a physically consistent model that, despite its simplifications, allows prediction of water flow dynamics in two structurally different basins.

7. Conclusion

• A hierarchical physically based storage and transmission model was designed as an alternative means for simulating continuous flow dynamics in complex engineered urban basins.
• The model ignores the complexity of the drainage network, while reproducing efficiently the flow dynamics at the different end-points.
• Two important modeling assumptions are: (i) the pipe network is replaced by an underground impervious area and thus overland flow and pipe discharge can be together modeled as a fast discharge linear reservoir, and (ii) the water diverted out of the sewer system through the different CSOs can be combined together through the hydraulic discharge function of a representative CSO.
• Therefore, their approach is ideal for repetitive tasks such as model calibration and optimization.
• In addition, the model can serve as the flow part of more complex models assessing complex diffuse pollution production and transfer processes.

Figures

Fig. 6. Sample hydrograph for the calibration period (a) and full validation period (b) for flow modeled at river outlet. Gray dashes are field measurements, solid lines are model predictions and precipitation rate is on the right abscissa of (b).

Fig. 7. Results of the sensitivity analysis. The model is sensitive to ksub; ksup and c to a lesser extent. The NS criterion is in black and NB in gray. All model parameters are scaled between 0 and 100.

Fig. 1. Schema of the WWTP catchment conceptualization. The pipe and channel netw reservoir. The other part of the rain jAp enters the pervious zone (Su), where it can ev framework applies for river basin modeling. In the case where the model is used to sim network, thereby modeling the drainage effect of the sewer system, which is in addition WWTP is replaced by the river. Symbols are explained in the text.

Fig. 8. Dominant pathways considered. Endpoints of the system are the river and the WWTP.

Table 1 Mathematical expressions of adopted fitting criteria functions e.g.,(Nash and Sutcliffe, 1970; Hingray et al., 2009; Schaefli and Gupta, 2007; Fenicia et al., 2007; Reusser et al., 2008). Zsim and Zobs are the modeled and observed values and n is the number of observations.

Table 2 Calibration parameters and the range of values considered. For the Monte-Carlo parameter optimization procedure, a uniform distribution was considered.

Fig. 2. Linear low partitioning function applied to the representative CSO. The maximum flow reaching the WWTP is limited by the threshold, Qlim . The excess is diverted out of the modeled pipe network.

Fig. 3. Two basins are studied. For the Vidy Bay WWTP (white), the catchment is fully artificial, and is composed of Lausanne’s pipe network. The other is the urban basin of the Vuachère river (gray). The two basins partly overlap.

Fig. 4. Sample of the hydrograph for the calibration period (a) and full validation period (b) for flow modeled at WWTP inlet. Gray dashes are field measurements, solid lines are model predictions and precipitation rate is on the right abscissa of (b).

Fig. 5. Comparison of flow modeled at the WWTP with the presented model (black) and the RS-3.0 model (gray).

Frequently asked questions

Q1. What are the main physical processes driving the discharge at the two basin end-points in this?

The dominant physical processes driving water discharge at the two basin end-points in this study are Hortonian runoff, evapotranspiration, and gravity-driven percolation to groundwater. 

Q2. What are the two important assumptions that can be used to simplify sewer hydrologic/hydraulic?

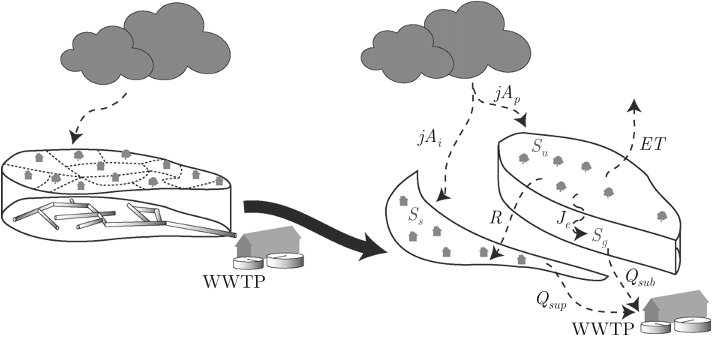
Two important modeling assumptions are: (i) the pipe network is replaced by an underground impervious area and thus overland flow and pipe discharge can be together modeled as a fast discharge linear reservoir, and (ii) the water diverted out of the sewer system through the different CSOs can be combined together through the hydraulic discharge function of a representative CSO. 

Q3. What is the common urban hydrological model used in research and engineering?

Most popular urban hydrological models used in research and engineering (e.g., MOUSE (Hernebring et al., 2002), SWMM3) are spatially distributed with link-node drainage networks. 

Q4. What is the purpose of the study?

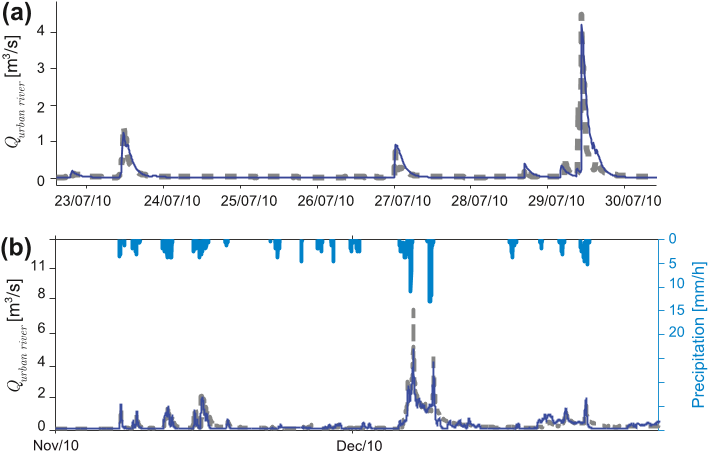
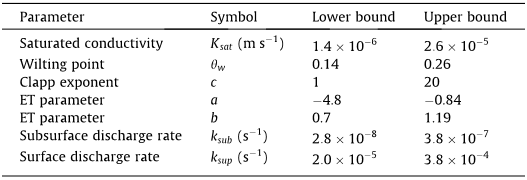
In this study, a hierarchical physically based storage and transmission model was designed as an alternative means for simulating continuous flow dynamics in complex engineered urban basins. 

Q5. What is the purpose of the model?

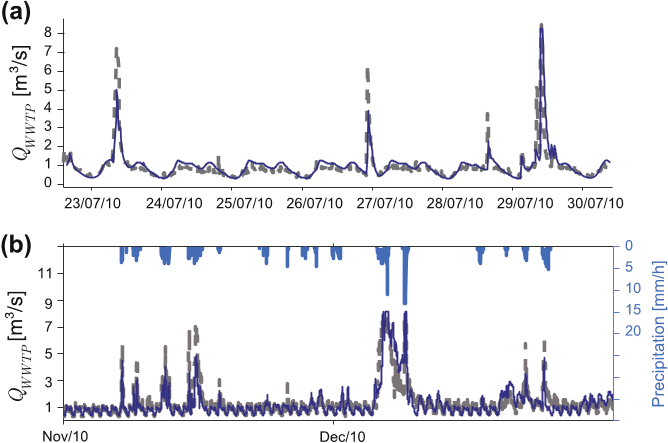
In addition, the hydrological model integrates functions that aim to reproduce characteristic daily variations of dry weather flow to the WWTP. 

Q6. Why is detailed modeling of drainage systems often deemed necessary?

Detailed modeling of drainage systems is often deemed necessary because of the complexity of flow paths in urban catchments (Cantone and Schmid, 2011; Gironás et al., 2009). 

Q7. What is the type of precipitation determined by the model?

The type of precipitation is determined based on a temperature threshold (DeWalle and Rango, 2008; Schaefli et al., 2005): when T is above the threshold Tcr , precipitation occurs as rain, otherwise precipitation is frozen. 

Q8. What is the closest CSO to the WWTP?

This CSO, the closest CSO to the WWTP, is responsible for more than a third of all CSO discharge, and is typically the first to become operational in storms (e-dric.ch, 2008). 

Q9. What is the model’s function for determining discharges at the WWTP inlet?

During dry weather, discharges arriving at the WWTP inlet are determined mainly by two phenomena: (i) infiltration of groundwater into the pipe network (see Section 2.2 and Dupont et al. (2006); Göbel et al. (2004)) and, (ii) water use and consequent wastewater production. 

Q10. What is the definition of a typical urban catchment?

It is a typical urban catchment, where much water comes from toilets, washing, industry and other uses, rather than directly from natural sources. 

Q11. What is the effect of the infiltration excess on the model?

Saturation excess was not implemented in their modeling scheme as the authors considered an unlimited reservoir height – i.e., the reservoir is never full – and this could lead to underestimation of surface runoff (Buda et al., 2009; MartínezMena et al., 1998; Nachabe et al., 1997).