




Did you find this useful? Give us your feedback










1 citations
1 citations
1 citations
2,993 citations
1,414 citations
...In summary, a bidirectional search of the task-constrained configuration space Ctask is performed by growing two Rapidly-exploring Random Trees (RRTs, see [21])....
[...]
1,260 citations
1,123 citations
1,007 citations
...Traditionally, task-constrained motion in configuration space for redundant robots is generated through kinematic control techniques [1], [2], [3], [4]....
[...]
For redundant robotic systems subject to repetitive task constraints, the authors have presented a control-based approach for planning cyclic, collision-free configuration space paths. Future work will be aimed at several objectives, such as: • the use of specific metrics for Ctask ; • a formal proof of probabilistic completeness for the planner ; • the extension of the proposed approach to robotic systems subject to nonholonomic constraints ( e. g., wheeled mobile manipulators ). The authors believe that their contribution fills a void in the literature.
The authors used4 N + 1 = 11 equispaced samples of the desired task path and generated motions using Euler’s method with integration step ∆s = 0.002.
Since the drawing task is 3-dimensional, the degree of redundancy is 6 − 3 = 3 (the wrist roll is frozen because it is irrelevant for the task).
At the end, the forward and backward trees contain 29 and 34 vertices, respectively, while the mean and the maximum task errors are 0.0275 mm and 0.0418 mm.
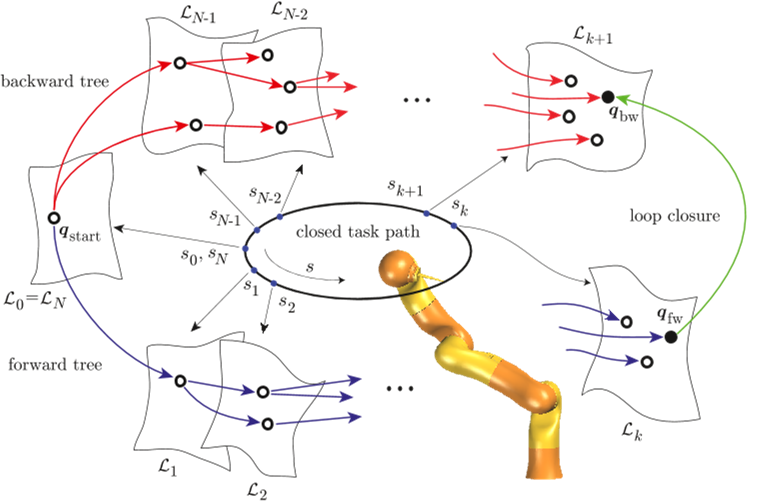
As customary in bidirectional search, extension steps are occasionally replaced (a parameter controls this event) by connection steps aimed at reducing the gap between the two trees.
When closure is obtained, a solution to the C-TCMP problem is reconstructed by patching together the subpath from qstart to qfw on Tfw, the loop closure subpath from qfw to qbw, and the subpath from qbw to qstart on Tbw (in the reverse direction).
The basic idea here is to identify a suitable subset of nq − nt ‘redundant’ configuration variables, and to perform the desired reconfiguration on these variables.
For redundant robotic systems subject to repetitive task constraints, the authors have presented a control-based approach for planning cyclic, collision-free configuration space paths.
Since the problem addressed in this paper is a special case of Task-Constrained Motion Planning (TCMP), the authors will adopt the terminology and framework introduced in [17].
At each iteration, a random configuration qrand is first generated3 in Ctask; this is done by picking a value for s ∈ {s1, . . . , sN−1}, and then choosing one of the inverse kinematic solutions for the corresponding sample of td(s).
For path or motion planning purposes, it is appropriate to use the geometric form of such model, which specifies the admissible tangent vectors to a configuration space path q(s), where s is a path parameter, asq′ = ṽ, (1)with the notation ( )′ = d( )/ds.
For each value of w̃, the motion generation scheme (3–4) is then integrated numerically starting from qnear at s = si and ending at s = si+1.
The mean and the maximum value of the task error norm over the whole path are, respectively, 0.0729 mm and 0.1354 mm, confirming that the proposed method guarantees continued satisfaction of the task constraint.
The authors emphasize that, unlike sampling-based constrained motion planners, the use of the motion generation scheme (3– 4) guarantees that the task variables move along the desired path throughout the motion.
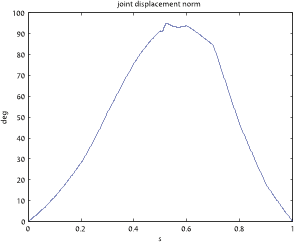
Cyclicity in configuration space is confirmed by Fig. 5, which shows that the displacement with respect to the initial configuration returns to zero at the end of the motion.
The solution shown in Fig. 3 took 83 s to compute, with a final size of the forward and backward trees of 116 and 33 vertices, respectively.
Future work will be aimed at several objectives, such as: • the use of specific metrics for Ctask; • a formal proof of probabilistic completeness for theplanner;• the extension of the proposed approach to robotic systems subject to nonholonomic constraints (e.g., wheeled mobile manipulators).