




Did you find this useful? Give us your feedback

![Figure 3: (A) Schematic representation of the uterus and the diffusive trajectory of the sperm that reaches an ovule. The possibility to form a zygote is determined by whether the time of the fastest sperm to reach the ovule is within the fertile period. (B) In a Brownian simulation in a schematic uterus, the trajectories with short arrival time are concentrated along two symmetric optimal paths (white dashed line) [14].](/figures/figure-3-a-schematic-representation-of-the-uterus-and-the-1vcj3wep.png)





13 citations
2 citations
160 citations
132 citations
80 citations
80 citations
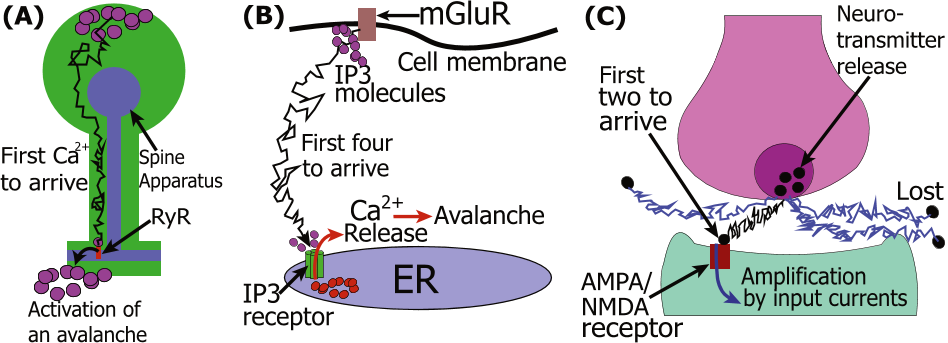
neuronal connections often occur on a dendritic spine, where the fast calcium increase in dendrites may happen a few milliseconds after initiation in the spine head.
The computation of the backward rate has long history that begins with Arrhenius’ law k−1 = AeE/kT , where A is a constant, and E is activation energy, then Kramers’ rate, derived from the molecular stochastic Langevin equation, which gives the prefactor A.
When particle move by diffusion, is it sufficient that the first particle arrives to a receptor to open it and lead to an avalanche either through the entry of ions or the opening of the neighboring receptors.
More specifically, mass-action theory of chemical reactions between two reactants insolution, A and B, is expressed asA k1 k−1 B,where k1 and k−1 are the forward and backward reaction rates, respectively.
Disproportionate numbers of particles in natural processes should not be considered wasteful, but rather, they serve a clear purpose: they are necessary for generating the fastest response.
The single particle survival probability isPr{t1 > t} = ∫ Ω p(x, t) dx, (5)so that Pr{τ 1 = t} = d dt Pr{τ 1 < t} = N(Pr{t1 > t})N−1 Pr{t1 = t}, where Pr{t1 = t} =∮∂Ωa∂p(x,t) ∂n dSx and Pr{t1 = t} = NR ∮ ∂Ω1 ∂p(x,t) ∂n dSx.
The number of spermatozoa is thus the main determinant of the selection and since the mean time for the first one to arrive is O(1/logN), a large number of them is necessary to affect the search process.
Activation occurs by the first particle to find a small target and the time scale for this activation uses very different geometrical features (optimal paths) than the one described by the traditional mass-action law, reaction-diffusion equations, or Markov-chain representation of stochastic chemical reactions.
Brownian trajectories (ions) in a bounded domain Ω to a binding site, the shortest arrival time τ 1 is by definitionτ 1 = min(t1, . . . , tN), (2)where ti are the i.i.d. arrival times of the N ions in the medium.
The asymptotic laws for the expected first arrival time ofBrownian particles to a target for large N , are,τ̄ d1 ≈ δ 2 min4D ln( N√ π ) , in dim 1 (8)τ̄ d2 ≈ ≈ s 2 24D log( π √ 2N8 log ( 1 ε)) , in dim 2 (9)τ̄ d3 ≈ δ 22D √ log ( N 4a2π1/2δ2) , in dim 3. (10)These formulas show that expected arrival time of the fastest particles is O(1/ log(N)) (see Fig. 2).