




Did you find this useful? Give us your feedback
![FIG. 1. Carter-Penrose diagrams of the spacelike stretched black hole spacetime for the case r0 < r− < r+ on the left and of the manifold M with mirrors described in the text on the right (adapted from Ref. [16]).](/figures/fig-1-carter-penrose-diagrams-of-the-spacelike-stretched-307om29m.png)





25 citations
21 citations
16 citations
9 citations
...With the notable exception of [23, 24, 29, 34], most of the works cited above concerned either asymptotically flat or asymptotically de Sitter black holes....
[...]
7 citations
...(An analytic approximation good for fields with large mass is available, however [8], and exact results are obtainable in d = 3 with AdS asymptotics [9, 10]....
[...]
6,464 citations
1,806 citations
1,793 citations
...One important task is the computation of expectation values of the renormalized stressenergy tensor for a matter field in a given quantum state [7, 8]....
[...]
460 citations
In the future, the authors intend to extend this method to compute the expectation value of the stress-energy tensor. The authors anticipate that this method can be extended to wider classes of rotating black hole spacetimes, and in particular in four dimensions to the Kerr spacetime.
The advantage of using the Minkowski spacetime is that its symmetries allow us to compute the Green’s function in both closed form and as a mode sum.
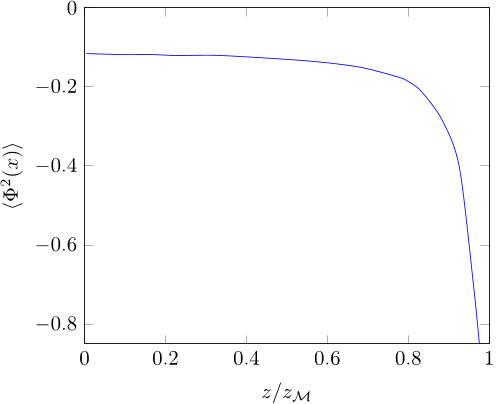
After this matching is performed, the vacuum polarization is just given by〈Φ2(x)〉 = lim θ̃→0 GBHren(x, x ′) , (3.28)which is a well-defined smooth function for x ∈ Ĩ.
In the context of quantum field theory, as it is detailed below, the nonexistence of an everywhere timelike Killing vector field in the exterior region of the spacetime is directly related to the nonexistence of a well defined quantum vacuum state which is regular at the horizon and is invariant under the isometries of the spacetime.
The dimensionless coupling ν ∈ (1,∞) is the warp factor, and in the limit ν → 1 the above metric reduces to the metric of the BTZ black hole in a rotating frame.
This is followed by a detailed account of the Hadamard renormalization procedure, in which the authors subtract the divergences in the mode sum by a sum over Minkowski modes with the same singularity structure.
To find the renormalized vacuum polarization in other Hadamard states of interest, such as the Boulware vacuum state, it would suffice to use the Hartle-Hawking state as a reference and just to calculate the difference, which is finite without further renormalization.
the singular, state-independent part of the Feynman propagator isGHad(x, x ′) :=i 4 √ 2π U(x, x′)√ σ(x, x′) + i . (2.21)This is known as the “Hadamard singular part” and it is singular at x′ → x.