




Did you find this useful? Give us your feedback










39 citations
17 citations
...At the surface of a granular bed, streamwise grooves can be generated by counterrotating vortices when the flow is turbulent [17,18] or by the diffusion-like transport of grains from the troughs to the crests of the bed in a laminar regime [19]....
[...]
11 citations
10 citations
7 citations
2,182 citations
...Accordingly, the sediment flux resulting from their collective motion, called bedload transport, is usually expressed as a function of shear stress (Meyer-Peter & Müller 1948)....
[...]
...Most authors relate bedload directly to the Shields parameter with a sediment transport law (Meyer-Peter & Müller 1948)....
[...]
1,309 citations
935 citations
...A natural question to ask, then, will be whether the bedload instability grows as far as to split a broad channel into smaller ones, thus creating the precursor of a braided river (Stebbings 1963; Métivier, Lajeunesse & Devauchelle 2017)....
[...]
876 citations
...For randomly packed spheres, the packing fraction is approximately φ∼ 0.6 (Bernal & Mason 1960)....
[...]
703 citations
...Current ripples are iconic underwater bedforms found in streams, on beaches and sometimes in the sedimentary record (Allen 1982; Coleman & Melville 1994)....
[...]
The authors speculate that this might not be fortuitous, as experimenters often wish the sediment bed to be invariant in the cross-stream direction. At this point, the authors can only imagine an ideal set-up, specially designed to observe the bedload instability. Once such a framework is set, it will become a matter of numerical routines to explore it beyond linearity.
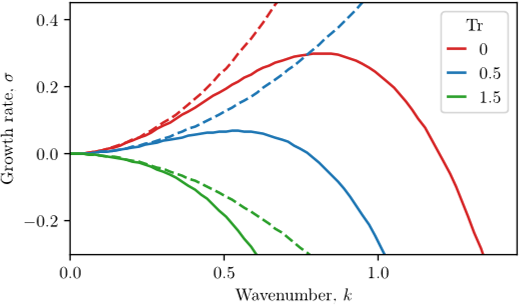
Stokes flowBedload diffusion reinforces streamwise streaks provided (i) bedload transport is weak, and (ii) the flow exerts a lower shear stress on the crests than in the troughs.
As long as the flow-induced force is comparable to their weight, the entrained grains remain close to the bed surface, where they travel with the flow, until they eventually settle down.
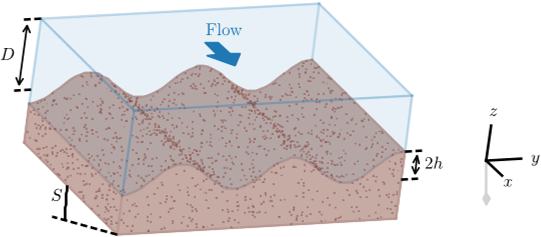
In steady state, the shear stress the fluid exerts on the bed, τ , is the projection of its weight on the streamwise direction:τ = ρgDS (2.1)where ρ is the density of the fluid, and g the acceleration of gravity.
The bedload instability is sensitive to boundary conditions; it persists in a rectangular pipe, but disappears when the flow is driven by a travelling lid.
Once the perturbation has outgrown hmax, the instability enters a nonlinear regime, to which the present analysis grants no access.
Over a granular bed, these slow secondary currents transport sediment across the primary flow to accumulate it in upwelling areas, thus reinforcing the ridges that brought them about.
The bedload density equation (2.7), the cross-stream flux equations (2.9) and (2.10), and the the Exner equation form a closed system, which the slope-induced flux makes nonlinear.
they diffuse across the bedload layer towards areas of lesser transport, thus moving across the stream in the absence of transverse flow.
Because it can only grow near the threshold of sediment transport, the unstable perturbation quickly enters a nonlinear regime which the authors havenot investigated.
When water flows over a granular bed with enough strength, it dislodges some of the superficial grains and entrains them downstream (Shields 1936; Einstein 1937; Bagnold 1973).
Although most bedload experiments involve open channels, the free surface of the flow makes the tracking of sediment grains difficult.
while the stabilising mechanism vanishes, the unstable coupling between the flow and the bed persists—the bedload instability then thrives.
In addition, the parameter γ, which accounts for the gravityinduced flux of sediment, has never been measured in a laminar flow (section 2.3).
In steady state, the balance between entrainment and settling sets the number of travelling grains, which thus depends primarily on the flow-induced shear stress (Charru et al. 2004a; Lajeunesse et al. 2010).
The pipe should be wider than the wavelength of the perturbation; an aspect ratio of approximately 20, for instance, should allow two parallel streaks to grow.
of course, raises the question of its actual existence, but the authors suspect that the basic reason for its absence from the literature is that the aspect ratio of laboratory channels is usually too small to accommodate its growth.
A reliable theory of bedload diffusion, tested against laboratory experiments, would therefore help us understand their morphology.
To identify the bedload instability unambiguously, one need only reduce the bedload flux until the wavelength of the instability reaches its minimum, which should be the above value.
Re ( ĥ exp ( ikyD))) , (4.6)thus confirming that, regardless of the wavenumber k, the shear stress is always stronger at the crest.
The linear stability analysis the authors have presented in this paper identifies a new instability associated with bedload transport, caused by the cross-stream diffusion of the travelling grains.
the accumulationof these steps generates a diffusive flux, qd, towards the less populated areas of the bedload layer.