




Did you find this useful? Give us your feedback









120 citations
74 citations
...0004 (the same value has been used in [15])....
[...]
...Note that we use a different definition of the surface elevation from the one in [15] where the 1/2 factor is not included (the consequence is that the coefficient in the nonlinear term in equation (2) differs by a factor of 4 from the one in equation (3....
[...]
...In [15] the equation is written in a nondimensional form and the coefficient K = Γ/ω0 is introduced)....
[...]
...We considered the NLS equation discussed in [15]...
[...]
...More recently, the role of dissipation and wind in the modulational instability has been considered together within the NLS equation, [15] (then confirmed by fully nonlinear simulations, [16])....
[...]
70 citations
63 citations
...The case ΓM/ f = O( 2) gives rise to the following damped/forced nonlinear Schrödinger equation [11, 8, 12]...
[...]
...For a logarithmic velocity profile in the boundary layer, the Miles growth rate ΓM results in [4, 7, 8]...
[...]
...The pressure P induced at the water surface then depends on the surface elevation η as follows [4, 8] 1 ρw P(x, t) = ΓM f c(2)p 2π ηx(x, t) (2)...
[...]
41 citations
... (2014). New terms which appear in that modification of the NLS equation may be eliminated after appropriate change of variables, and then the equation turns to the form considered in (Leblanc, 2007; Kharif et al, 2010; Onorato & Proment, 2012). Numerical simulations of individual wave groups affected by wind were performed within different frameworks in (Yan and Ma, 2010; Adcock and Taylor, 2011). Laboratory a...
[...]
56 citations
...Conte & Miles (1959) developed a numerical method to treat this singularity and solve the Rayleigh equation....
[...]
...Conte & Miles (1959) computed the values of β as a function of κc0/u∗ for a logarithmic wind profile of the form U (z) = u∗ κ ln(z/z0), (3.7) where z0 is the roughness length given by z0 = αchu 2 ∗/g (αch is the Charnock constant ≈0.011–0.018)....
[...]
42 citations
...Following Miles (1996), the coefficient β is given by the following expression: β = −π k (d2U/dz2)(zc) |(dU/dz)(zc)| w2(zc) U 21 (∂η/∂x) 2 , (2.10) where z = η(x) is the equation of the surface wave profile....
[...]
41 citations
...In the regime we are considering, we have shown that the effect of the wind is contrary, as expected (Leblanc 2007)....
[...]
...Our aim is to extend the works of Segur et al. (2005a) and Leblanc (2007) who investigated this problem by considering damping and wind effects separately....
[...]
...To study the modulational stability of this solution we follow Segur et al. (2005a) and Leblanc (2007), and we superimpose to the solution (4.1) a small perturbation Ψ = Ψs(1 + δζ (ξ, τ )), (4.4) where δ 1....
[...]
The evolution of a two-dimensional nonlinear wave train on deep water, in the absence of dissipative effects, exhibits the Fermi–Pasta–Ulam recurrence phenomenon.
Since damping affects the modulational instability of waves in deep water, they assumed that it might affect the early development of rogue waves.
For an energy flux to occur from the wind to the water waves, there must be a phase shift between the fluctuating pressure and the interface.
The present paper is aimed at reporting on the behaviour of Benjamin–Feir instability when dissipation and wind input are both taken into account.
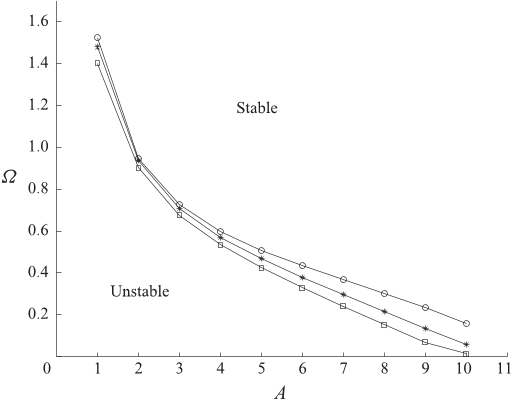
In the presence of wind and dissipation, the unstable domain shrinks for low-frequency regime: this means that young waves are more sensitive to modulational instability than old waves.
Email address for correspondence: kharif@irphe.univ-mrs.frnearly uniform wave trains become modulated and then demodulated until they are again nearly uniform.
when the perturbations are small initially, they cannot grow large enough for nonlinear resonant interaction between the carrier and the sidebands to become important.
Since Stokes (1847), it is well known that the potential water wave problem admits as solutions uniform wave trains of two-dimensional progressive waves.
This situation was discussed by Segur et al. (2005a, see their comment (iii) p. 238), and it was claimed that even with substantial growth of the perturbation, the Stokes solution of (3.4) is still linearly stable: it is always possible to find a gap (denoted ∆) between unperturbed and perturbed solution that satisfies the linear stability criterion.