



read more









The skin-effect results from eddy currents within the wire that counteract the current in the core, and forces the current to the surface of the wire.
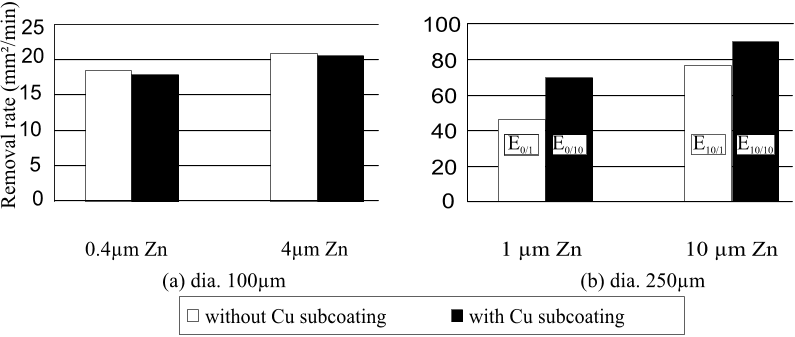
Since the coating is substantially less electrical resistant than the steel core, most of the Joule heating power will be dissipated in the coating.
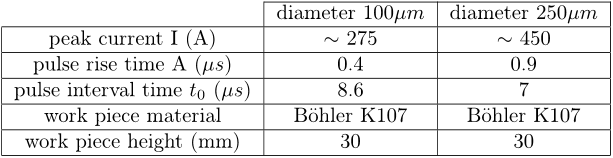
For the steel wire of diameter 100µm the influence of the skin-effect is less, it yields an increase of the resistance by a factor 2 to 3, resulting in a value which is 30 times as high as a copper wire.
A voltage source delivers a current that depends on the load: impedance of the machine, the wire, the gap and the work piece, which is a disadvantage while compared to current sources, who are supposed to deliver a fixed current independently of the process’s impedance.
It is also mentioned that conductive coatings out of non-permeable materials on top of steel wires lower the impedance even at high frequencies.
The frequency dependence of a wire’s internal inductance is approximately given by equation 5, with ξ given by equation 2.2πνL R0 ≈ ξ2 − ξ66 if ξ << 12πνL R0 ≈ ξ − 3 64ξ + 3 128ξ3 if ξ >> 1 (5)The wire’s inductance L0 at low frequencies equals µ 8π [7].
The internal inductance of a coated a-magnetic wire can be calculated by calculating the energy stored in the magnetic field inside the wire.
Since the resistance of a steel wire at the frequencies under consideration seems to be independent of carbon content, the 0.7%C wire can be chosen to profit from its higher tensile strength in precision applications [6, 8].
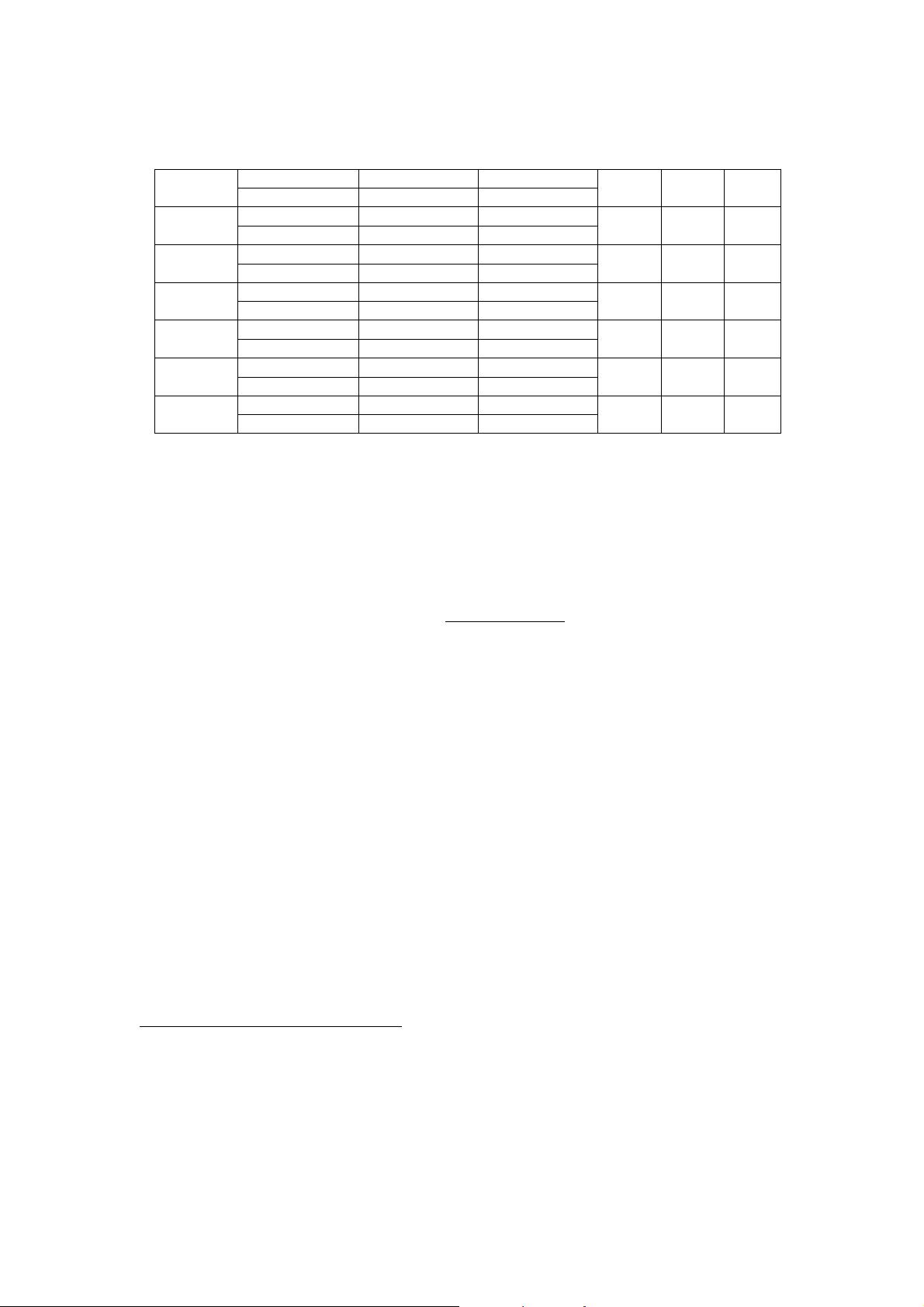
When calculated for a steel wire (0.7%C) with a 4 µm Zn-coating the D.C. resistance is 17.32 Ω/m, compared to 22.73 Ω/m without coating.
Since all known coatings (Cu, CuZnx, Zn,...) are a-magnetic, the skin-effect can be neglected in the calculation of the resistance of the coating.
For thick coatings the D.C. as well as the high frequency resistances are comparable to those of plain brass wires, while the tensile strength of their cores stays considerably higher.
This means that e.g. a plain steel wire with high resistance will be weakened and broken even at lower peak currents (erosion energy), and hence lower speed, than a coated steel wire which has low resistance.
For a coating with outer radius ro and inner radius ri it is given byRcoating = 1σcoatingπ(r2o − r2i ) (4)The total value of the wire’s resistance is then found by assuming that the core of the wire is electrically parallel to the coating.
The dropping of the inductance due to the skin-effect in steel wires, as explained in section 2.2.1, will be counteracted by using a thin conductive coating which is non-permeable (copper, brass, zinc, . . . ) in the same way the rising of the resistance in counteracted.
It has been shown by the examination of the wire’s impedance, that the skin-effect becomes a predominant phenomenon in wire-EDM, while machining with ferro-magnetic wires.
In this sense the resistance electrically parallel to the steel core is smaller and less able to lower the total resistance of the wire.