




Did you find this useful? Give us your feedback
















43 citations
3 citations
257 citations
227 citations
188 citations
180 citations
156 citations
This promising result of the global stability analysis can, in turn, be a basis for future efforts aiming at the detection of this instability and thereby providing an experimental evidence for its existence. Building on the findings of this first study, future work will explore in greater detail the parameter space and the effect of boundary conditions on type 2 Super-HMRI, which are more relevant to those present in TC flow experiments.
Energy is drawn from the background flow rΩ(r) to the growing perturbations due to the coupling between meridional circulation and azimuthal field perturbations brought about by the imposed azimuthal field, a mechanism also underlying HMRI at negative shear [6, 29].
The imposed background helical magnetic field B0 = (0, B0φ(r), B0z) consists of a radially varying, current-free azimuthal component, B0φ(r) = βB0zro/r, and a constant axial component, B0z , where the constant parameter β characterizes field’s helicity.
A basic condition for the local WKB approximation to hold is that the radial wavelength, λr, of the perturbations must be much smaller than the characteristic radial size, ro, of the system over which the equilibrium quantities vary, i.e., λr ≪ ro.
Since the authors focus on positive Rossby numbers, Ro > 0, or positive shear, the flow is generally stable both hydrodynamically, according to Rayleigh’s criterion (but see Ref. [13]), as well as against SMRI with a purely axial field (β = 0) [24–26].
depending on Ha and Re, conducting boundaries can lead either to increase or decrease of the growth rate compared to its WKB value, whereas insulating boundaries alwaysreduce the growth rate about three times compared to those for the conducting ones for fixed Hartmann and Reynolds numbers.
Since the authors are primarily interested in the flow stability in the case of positive shear, or so-called “super-rotation” [15, 16], the inner cylinder is assumed to rotate slower than the outer one, Ωi < Ωo, inducing an azimuthal nonuniform flow U0 = (0, rΩ(r), 0) between the cylinders with radially increasing angular velocity, dΩ/dr > 0, and hence positive Rossby number, Ro > 0.
In this section, the authors use a radially local WKB approximation, where the radial dependence of the perturbations is assumed to be of the form ∝ exp(ikrr) with kr being the radial wavenumber.
Another reason for the differences in the growth rates between the local and the global wide gap cases is that a finite distance between the cylinders also excludes (cuts off) very small radial wavenumbers (α → 1), which correspond to larger growth rates at β ∼ 1 in the WKB analysis (see Fig. 1(b)).
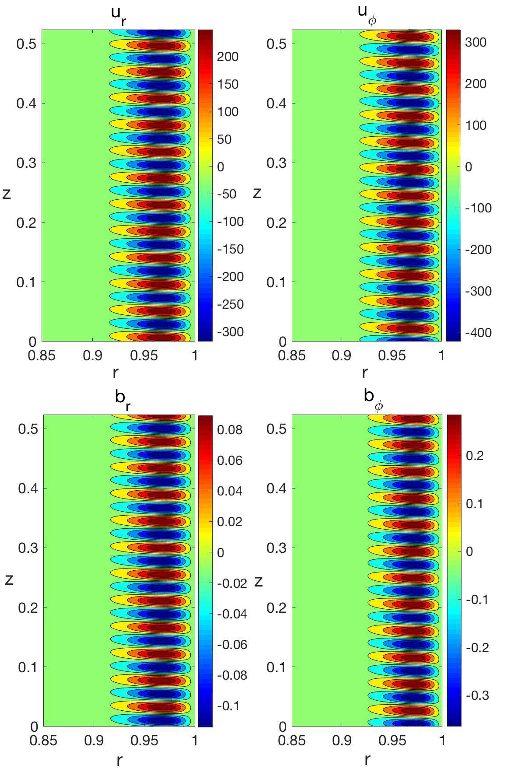
As noted above, in this subsection, the primary goal of these calculations is to identify this new instability in a TC flow setup commonly employed in lab experiments, which in the present case has a radially increasing angular velocity (positive shear) profile.
Regarding the dependence on β parameter in Eq. (4), it is readily seen that, as long as β 6= 0, it enters the coefficients of these dispersion relations through the re-scaled wavenumbers, Hartmann, Lundquist and Reynolds numbers, k∗z ≡ kz/β, k∗ ≡ k/β, Ha∗ ≡ Ha/β, S∗ ≡ S/β, Re∗ ≡ Re/β2, Rm∗ ≡ Rm/β2, in terms of which the authors carry out the following WKB analysis.
type 2 Super-HMRI represents a new, dissipation-induced instability mode at positive shear, which appears to require the presence of both finite viscosity and resistivity.
This latter branch is basically an extension of the more familiar HMRI operating at negative shear, which in the inductionless limit also satisfies Eq. (5), but at Ro < RoLLL, where RoLLL = 2(1 − √2) ≈ −0.83 is the lower Liu limit [19, 24, 27].
The authors take β ∼ 1 in these calculations for the wide-gap, since it is rather costly to achieve large β in experiments due to very high axial currents required.
In particular, the maximum growth rate, γm, occurs for (Ha ∗ m, Re ∗m) ≈ (700, 9 · 104) when Pm is small (Fig. 1(c)), but for orders of magnitude smaller (Ha∗m, Re ∗m) = (2.54, 0.23) when Pm is large (Fig. 2(c))
the authors will see in the global linear analysis below that this mode of instability is in fact not restricted only to large β and can even exist at smaller β ∼ 1, but in this case the WKB approach is questionable and should be applied with caution.