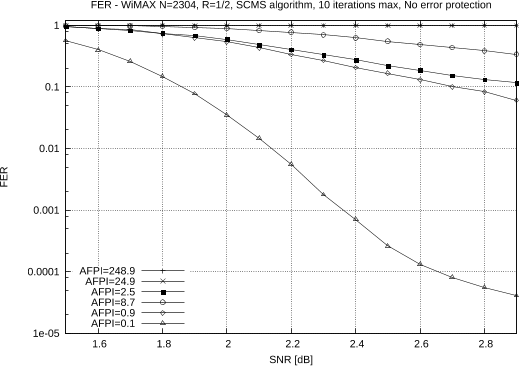
Abstract: With scaling of process technologies and increase in process variations, embedded memories will be inherently unreliable. Approximate computing is a new class of techniques that relax the accuracy requirement of computing systems. In this paper, we present the A daptive Co ding for approximate Co mputing (ACOCO) framework, which provides us with an analysis-guided design methodology to develop adaptive codes for different computations on the data read from faulty memories. In ACOCO, we first compress the data by introducing distortion in the source encoder, and then add redundant bits to protect the data against memory errors in the channel encoder. We are thus able to protect the data against memory errors without additional memory overhead so that the coded data have the same bit-length as the uncoded data. We design the source encoder by first specifying a cost function measuring the effect of the data compression on the system output, and then design the source code according to this cost function. We develop adaptive codes for two types of systems under ACOCO. The first type of systems we consider, which includes many machine learning and graph-based inference systems, is the systems dominated by product operations. We evaluate the cost function statistics for the proposed adaptive codes, and demonstrate its effectiveness via two application examples: max-product image denoising and naive Bayesian classification. Next, we consider another type of systems: iterative decoders with min operation and sign-bit decision, which are widely applied in wireless communication systems. We develop an adaptive coding scheme for the min-sum decoder subject to memory errors. A density evolution analysis and simulations on finite length codes both demonstrate that the decoder with our adaptive code achieves a residual error rate that is on the order of the square of the residual error rate achieved by the nominal min-sum decoder.