




Did you find this useful? Give us your feedback












40 citations
28 citations
24 citations
23 citations
20 citations
The rock (or stone) breaking and crushing process plays an important role in minimizing the particle size of stone or rock for various construction activities, such as building bridges or infrastructure.
The vibration that occurred during the operation of the screen unit and sand units is transmitted the power to the shaft through the belt pulley directly related to the excitation force generated by actuating motors.
The vibration isolation for the artificial sand production plant is mainly achieved by utilizing rubber mounts and/or coil springs.
indiscriminate collection of sand from rivers causes flooding and destruction of the natural environment such as river ecosystems, leading to various social issues.
More specifically, for the sand unit, VAL, ∆VAL, transmissibility and percent isolation are calculated by 116 dB, 31 dB, 0.028, and 97.2%, respectively.
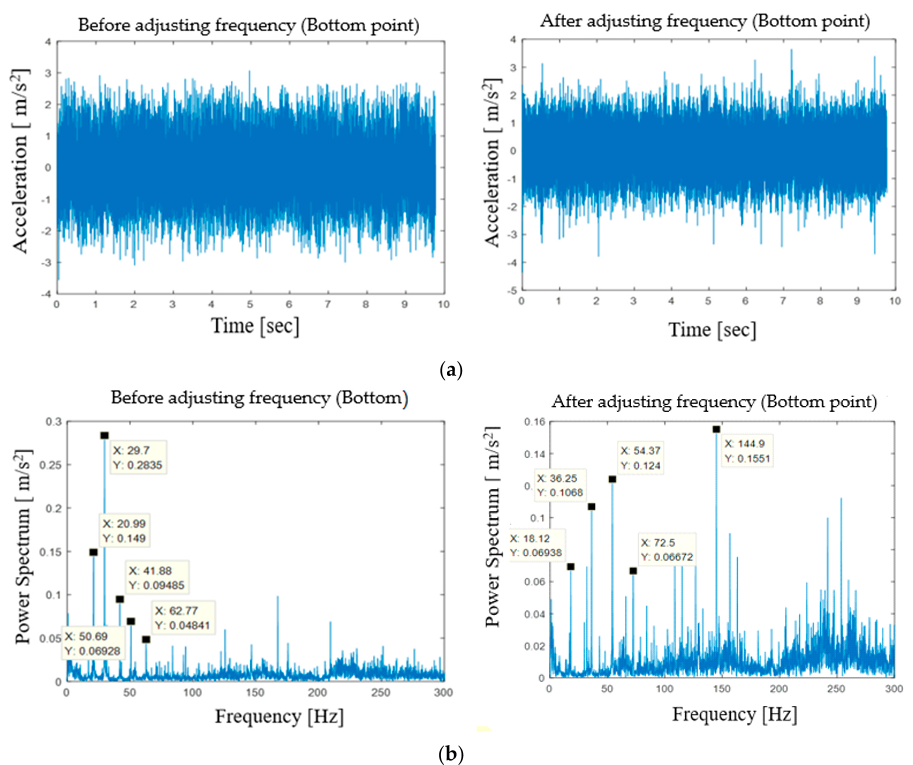
In this work, the beating phenomenon can occur by resonance when the fundamental frequencies corresponding to the driving frequencies of sand and screen unit actuators are close.
The example of passive isolators in a mechanical system includes metal coil spring, cork, felt, pneumatic springs and viscoelastic material, such as elastomer or rubber springs.
The vibration acceleration level (VAL) at the upper point of the coil spring is calculated by 150 dB, and the VAL at the bottom point of the coil spring is by 140 dB, respectively.
The vibration isolation design has three criteria or requirements as follows [32–38]: (i) the frequency ratio should be more than three (f /fn = r ≥ 3), (ii) the vibration transmissibility (or percentage isolation) should be below 0.1 (%I ≥ 90%, where, %I represents the vibration isolation rate percentage) (iii) the minimum value of the vibration isolation efficiency should be under 12.5%.
Appl. Sci. 2020, 10, 4327 3 of 17Consequently, the main technical contribution of this work is to experimentally investigate the vibration characteristics of the artificial sand production plant through on-site measurement.
Based on Equation (4), the calculated VAL at the top point of the coil spring is 147 dB, and the calculated VAL at the bottom point of the coil spring is 116 dB, respectively.
the occurrence of the beating behavior is seriously considered as one of the main reasons which can cause high vibration levels.
Appl. Sci. 2020, 10, 4327 4 of 17Appl. Sci. 2020, 10, x FOR PEER REVIEW 3 of 17 isolations of the sand and screen units are evaluated, and vibration sources are identified.