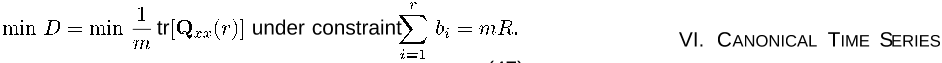IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 46, NO. 3, MARCH 1998 647
Wiener Filters in Canonical Coordinates for
Transform Coding, Filtering, and Quantizing
Louis L. Scharf, Fellow, IEEE, and John K. Thomas
Abstract— Canonical correlations are used to decompose the
Wiener filter into a whitening transform coder, a canonical filter,
and a coloring transform decoder. The outputs of the whitening
transform coder are called canonical coordinates; these are the
coordinates that are reduced in rank and quantized in our
finite-precision version of the Gauss–Markov theorem. Canonical
correlations are, in fact, cosines of the canonical angles between
a source vector and a measurement vector. They produce new
formulas for error covariance, spectral flatness, and entropy.
Index Terms—Adaptive filtering, canonical coordinates, canon-
ical correlations, quantizing, transform coding, Wiener filters.
I. INTRODUCTION
C
ANONICAL correlations were introduced by Hotelling
[1], [2] and further developed by Anderson [3]. They are
now a standard topic in texts on multivariate analysis [4], [5].
Canonical correlations are closely related to coherency spectra,
and these spectra have engaged the interest of acousticians
and others for decades. In this paper, we take a fresh look at
canonical correlations, in a filtering context, and discover that
they provide a natural decomposition of the Wiener filter. In
this decomposition, the singular value decomposition (SVD)
of a coherence matrix plays a central role: The right singular
vectors are used in a whitening transform coder to produce
canonical coordinates of the measurement vector; the diagonal
singular value matrix is used as a canonical Wiener filter to
estimate the canonical source coordinates from the canonical
measurement coordinates; and the left singular vectors are used
in a coloring transform decoder to reconstruct the estimate of
the source. The canonical source coordinates and the canonical
measurement coordinates are white, but their cross correlation
is the diagonal singular value matrix of the SVD, which is
also called the canonical correlation matrix.
The Wiener filter is reduced in rank by purging subdominant
canonical measurement coordinates that have small squared-
canonical correlation with the canonical source coordinates.
Quantizing is done by independently quantizing the canonical
Manuscript received September 24, 1996; revised May 21, 1997. This work
supported by the National Science Foundation under Contract MIP-9529050
and by the Office of Naval Research under Contract N00014-89-J-1070. The
associate editor coordinating the review of this paper and approving it for
publication was Dr. Jos
´
e Principe.
L. L. Scharf is with the Department of Electrical and Computer Engi-
neering, University of Colorado, Boulder, CO 80309-0425 USA (e-mail:
scharf@boulder.colorado.edu).
J. K. Thomas is with the Data Fusion Corporation, Westminster, CO 80021
USA (e-mail: thomasjk@datafusion.com).
Publisher Item Identifier S 1053-587X(98)01999-0.
measurement coordinates to produce a quantized Wiener filter
or a quantized Gauss–Markov theorem.
The abstract motivation for studying canonical correlations
is that they provide a minimal description of the correlation
between a source vector and a measurement vector. Canonical
correlations are also cosines of canonical angles; therefore,
some very illuminating geometrical insights are gained from a
study of Wiener filters in canonical coordinates. The concrete
motivation for studying canonical correlations is that they are
the variables that determine how a Wiener filter can be reduced
in rank and quantized for a finite-precision implementation.
Canonical correlations decompose formulas for error co-
variance, spectral flatness, and entropy, and they produce
geometrical interpretations of all three. These decompositions
show that canonical correlations play the role of direction
cosines between random vectors, lending new insights into
old formulas. All of these finite-dimensional results generalize
to cyclic time series and to wide-sense stationary time series.
Finally, experimental training data may be used in place of
second-order information to produce formulas for adaptive
Wiener filters in adaptive canonical coordinates.
II. P
RELIMINARY OBSERVATIONS
Let us begin our discussion of canonical coordinates by
revisiting an old problem in linear prediction. The zero-
mean random vector
has covariance matrix
(1)
The determinant of
may be written as
(2)
where
is the error variance for estimating the scalar
from the vector . This error variance may be written
as
(3)
(4)
We call
the squared coherence between the scalar
and the vector because it may be written as the product
(5)
(6)
1053–587X/98$10.00 1998 IEEE
648 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 46, NO. 3, MARCH 1998
The vector is the coherence between and ,
or the cross correlation between the white random scalar
and the white random vector :
(7)
This basic idea may be iterated to write
as
(8)
(9)
where
is the squared coherence between the scalar
and the vector . This formula for
is the Gram determinant, with each prediction error
variance written in terms of squared coherence. It provides a
fine-grained resolution of entropy and spectral flatness:
(10)
(11)
Therefore, entropy is near its maximum, and spectral flatness
is near 1 when the squared coherences between
and
are near zero for all .
The sequence of Wiener filters that underlies this decompo-
sition of
is
(12)
which is a decomposition of the filter into a whitener
, a coherence filter , and a colorer .
This idea is fundamental.
III. C
ANONICAL CORRELATIONS IN A FILTERING CONTEXT
The context for our further development of canonical cor-
relations is illustrated in Fig. 1. The
source vector
and the measurement vector are generated by Mother
Nature. Father Nature views only the measurement vector
,
and from it, he must estimate Mother Nature’s source vector
. This problem is meaningful because the zero-mean random
vectors
and share the covariance matrix :
(13)
Fig. 1. Filtering problem.
(a)
(b)
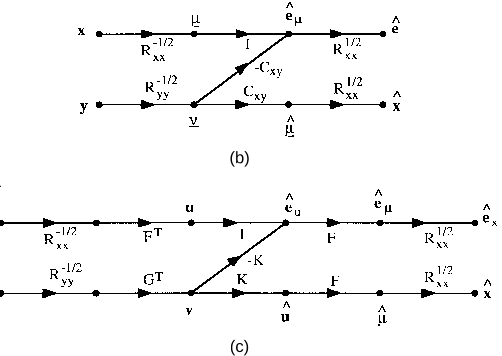
(c)
Fig. 2. Wiener filter in various coordinate systems.
A. Standard Coordinates
The linear MMSE estimator of
from is , and
the corresponding (orthogonal) error is
. In standard
coordinates, the Wiener filter
and the error covariance
matrix
are
(14)
(15)
We shall call Fig. 2(a) the Wiener filter in standard coordi-
nates.
The linear transformation
(16)
resolves the source vector
and the measurement vector
into orthogonal vectors and , with respective covariances
and
(17)
This is one of the Schur decompositions of
. From this
formula, it follows that
may be written as
(18)
(19)
SCHARF AND THOMAS: WIENER FILTERS IN CANONICAL COORDINATES FOR TRANSFORM CODING, FILTERING, AND QUANTIZING 649
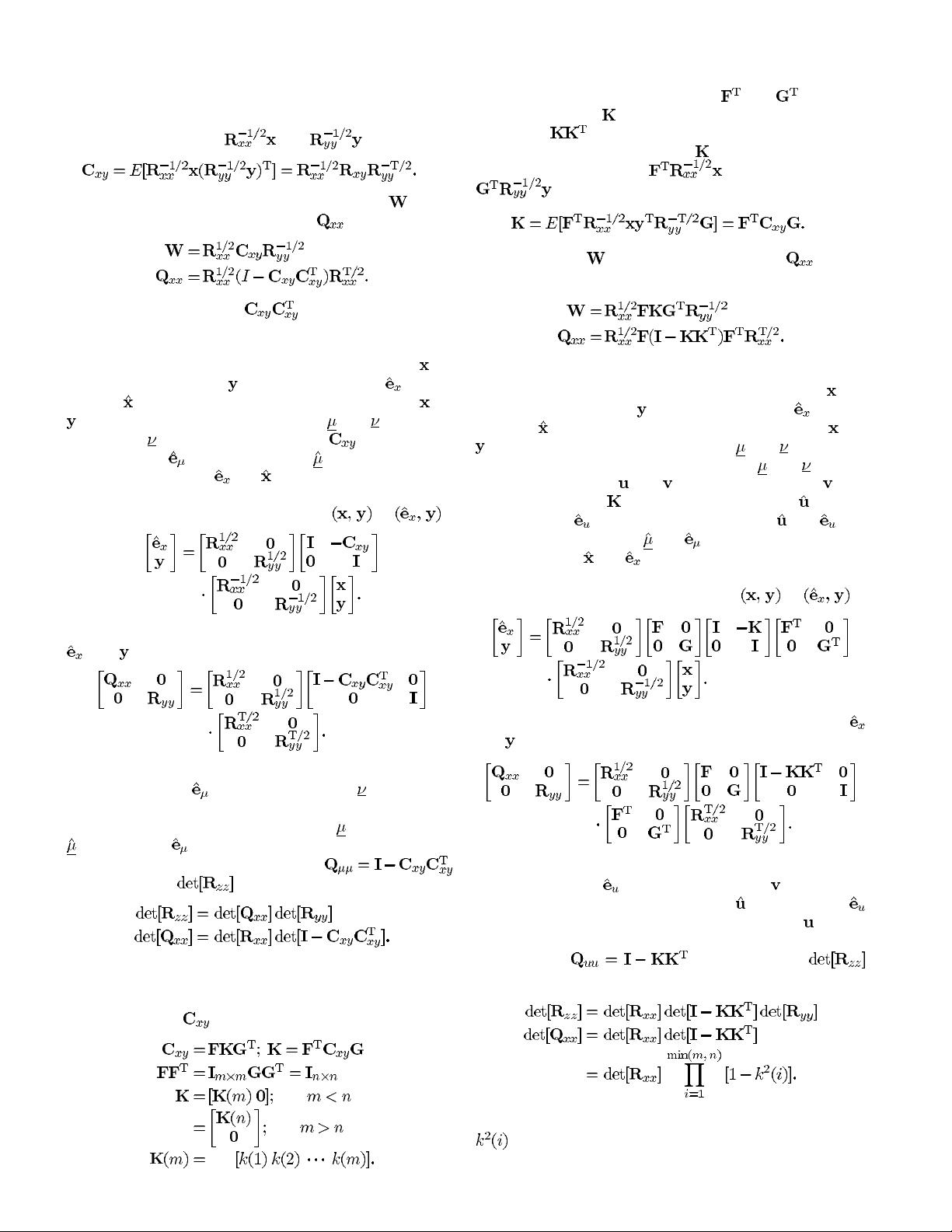
B. Coherence Coordinates
The coherence matrix measures the cross-correlation be-
tween the white vectors
and :
(20)
Using coherence, we can refine the Wiener filter
and its
corresponding error covariance matrix
as
(21)
(22)
We shall call the matrix
the squared coherence
matrix.
The corresponding Wiener filter, in coherence coordinates,
is illustrated in Fig. 2(b). It resolves the source vector
and
the measurement vector
into the error vector and the
estimate
in three stages. The first stage whitens both and
to produce the coherence coordinates and , the second
stage filters
with the coherence filter to produce the
estimator error
and the estimator , and the third stage
colors these to produce
and . We shall call this the Wiener
filter in coherence coordinates.
The refined linear transformation from
to is
(23)
The corresponding refinement for the covariance matrix for
and is
(24)
The diagonal structure of this covariance matrix shows that
the estimator error
and the measurement , in coherence
coordinates, are also uncorrelated, providing an orthogonal
decomposition of the coherence coordinate
into the estimator
and the error . It also shows that the covariance matrix
for the error in coherence coordinates is
.
The formula for
is now
(25)
(26)
C. Canonical Coordinates
We achieve one more level of refinement by replacing the
coherence matrix
by its SVD:
(27)
(28)
diag (29)
We shall call the orthogonal matrices
and transform
coders, the matrix
the canonical correlation matrix, and
the matrix
the squared canonical correlation matrix.
The canonical correlation matrix
is the cross correlation
between the white vector
and the white vector
:
(30)
The Wiener filter
and error covariance matrix in these
canonical coordinates are
(31)
(32)
The corresponding Wiener filter, in canonical coordinates, is
illustrated in Fig. 2(c). It resolves the source vector
and
the measurement vector
into the error vector and the
estimator
in five stages. The first stage whitens both and
to produce the coherence coordinates and , the second
stage transforms the coherence coordinates
and into the
canonical coordinates
and , the third stage filters with
the canonical filter
to produce the estimator and the
estimator error
, the fourth stage transforms and into
the coherence coordinates
and , and the fifth stage colors
these to produce
and . We shall call this the Wiener filter
in canonical coordinates.
The refined linear transformation from
to is
(33)
The corresponding refinement of the covariance matrix for
and is
(34)
The diagonal structure of this covariance matrix shows that
the estimator error
and the measurement are also un-
correlated, meaning that the estimator
and the error
orthogonally decompose the canonical coordinate . It also
shows that the covariance matrix for the error in canonical
coordinates is
. The formula for
is now
(35)
(36)
This formula shows that the squared canonical correlations
are objects of fundamental importance for filtering. We
pursue this point in Section IV.

650 IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 46, NO. 3, MARCH 1998
IV. FILTERING FORMULAS IN CANONICAL COORDINATES
We summarize as follows. The Wiener filter in canonical
coordinates replaces the source and measurement vectors in
standard coordinates with source and measurement vectors
in canonical coordinates. In these coordinates, the source
and measurement are white but diagonally cross correlated
according to the canonical correlation matrix
. This canon-
ical correlation matrix is also the Wiener filter for estimating
the canonical source coordinates from the canonical mea-
surement coordinates. The error covariance matrix associated
with Wiener filtering in these canonical coordinates is just
.
Recall that the canonical correlations are defined as
(37)
(38)
so that each canonical correlation
measures the cosine
of the angle between two unit variance random variables: one
drawn from the canonical source coordinates and one drawn
from the canonical measurement coordinates. For this reason,
we call the squared canonical correlations
direction
cosines. By making the canonical variables diagonally cor-
related, we have uncoupled the measurement of one direction
cosine from the measurement of another.
A. Linear Dependence
We think of the Hadamard ratio
as a
measure of linear dependence of the variables
and . Using
the results of (8) and (35), we may write the Hadamard ratio
as the product
(39)
This formula tells us that what matters is the intradependence
within
as measured by its direction cosines, the in-
tradependence within
as measured by its direction cosines,
and the interdependence between
and as measured by the
direction cosines between
and . These latter direction
cosines are measured in canonical coordinates, much as
principal angles between subspaces are measured in something
akin to canonical coordinates. They are scale invariant.
B. Relative Filtering Errors
The prior error covariance for the message vector
is ,
and the posterior error covariance for the error
is
. The volumes of the concentration ellipses associated with
these covariances are proportional to
and .
The relative volumes depend only on the direction cosines
:
(40)
C. Entropy and Rate
The entropy of the random vector
is
(41)
Normally, we write this entropy as the conditional entropy of
given , plus the entropy of . The conditional entropy, or
equivocation, is therefore
(42)
and the direction cosines determine how
brings information
about
to reduce its entropy from its prior value of .
The second term on the right-hand side of this equation is
the negative of rate in canonical coordinates. Thus, the rate
at which
brings information about is determined by the
direction cosines or squared canonical correlations between
the source and the measurement.
V. R
ANK REDUCTION FOR TRANSFORM
CODING,FILTERING, AND QUANTIZING
The Wiener filter in canonical coordinates is a filterbank
idea. That is, the measurement is decomposed into canonical
coordinates that bring information about the canonical coordi-
nates of the source. It is also a spread-spectrum idea because
the canonical coordinates are white. The question of rank
reduction and bit allocation for finite-precision Wiener filtering
or, equivalently, for source coding from noisy measurements is
clarified in canonical coordinates. The problem is to quantize
the canonical coordinates
so that the trace of the error
covariance matrix
is minimized. The error covariance
matrix and its trace are
(43)
tr
(44)
where the
are the energies of the “impulse responses”
for the coloring (or synthesizing) transform decoder:
(45)
If the canonical measurement coordinates
that are weakly
correlated with the canonical source coordinates are purged

SCHARF AND THOMAS: WIENER FILTERS IN CANONICAL COORDINATES FOR TRANSFORM CODING, FILTERING, AND QUANTIZING 651
and the remaining are uniformly quantized with bits, then
the resulting error covariance matrix for estimating the source
vector
from the reduced-rank and quantized canonical mea-
surement vector
is
tr
(46)
In this latter form, we observe that tr
consists of three
terms: the infinite-precision filtering error, the bias-squared
introduced by rank reduction, and the variance introduced by
quantizing. The trick is to properly balance the second and
third. To this end, we will consider the rate-distortion problem
tr under constraint
(47)
Using the standard procedure for minimizing with constraint
(see, for example, [9] and [10]), we obtain the solution
(48)
(49)
(50)
(51)
These formulas generalize the formulas of [9] by providing a
solution to the problem of uniformly quantizing the Wiener
filter or quantizing the Gauss–Markov theorem. They may be
interpreted as follows.
If the bit rate
is specified, then the slicing level
is adjusted to achieve it. The slicing level determines the
bit allocation
, the rank , and the minimum achievable
distortion
. Conversely, if the distortion is specified, is
adjusted to achieve it. This determines
, , and the minimum
rate
. These formulas are illustrated in Fig. 3 for the idealized
case where the
are unity. The components of distortion
illustrate the tradeoff between bias and variance.
(a) (b)
(c) (d)
Fig. 3. Components of distortion. (a) Squared canonical correlation. (b)
Infinite-precision distortion. (c) Extra components of distortion due to rank
reduction and quantizing. (d) Finite-precision distortion.
VI. CANONICAL TIME SERIES
If and are jointly stationary random vectors whose
dimensions increase without bound (that is, they are stationary
time series), then all of the correlation matrices in these formu-
las are infinite Toeplitz matrices with Fourier representations
(52)
Furthermore, if the time series are not perfectly predictable
(that is, the power spectra
and satisfy the Sz
¨
ego
conditions), then
and may be spectrally
factored as
(53)
where the filters
and are minimum phase, meaning
that
, , , and are causal and stable
filters. Then, the various square roots in the filtering fomulas
have the Fourier representations
(54a)
(54b)
(54c)
The SVD representation for
becomes a Fourier represen-
tation; therefore
(55)