PUBLISHED VERSION
Lerche, Christoph; von Smekal, Lorenz Johann Maria
Infrared exponent for gluon and ghost propagation in Landau gauge QCD Physical Review
D, 2002; 65(12):125006
©2002 American Physical Society
http://link.aps.org/doi/10.1103/PhysRevD.65.125006
http://link.aps.org/doi/10.1103/PhysRevD.62.093023
http://hdl.handle.net/2440/34444
PERMISSIONS
http://publish.aps.org/authors/transfer-of-copyright-agreement
“The author(s), and in the case of a Work Made For Hire, as defined in the U.S.
Copyright Act, 17 U.S.C.
§101, the employer named [below], shall have the following rights (the “Author Rights”):
[...]
3. The right to use all or part of the Article, including the APS-prepared version without
revision or modification, on the author(s)’ web home page or employer’s website and to
make copies of all or part of the Article, including the APS-prepared version without
revision or modification, for the author(s)’ and/or the employer’s use for educational or
research purposes.”
20
th
May 2013

Infrared exponent for gluon and ghost propagation in Landau gauge QCD
Christoph Lerche
*
and Lorenz von Smekal
†
Institut fu
¨
r Theoretische Physik III, Universita
¨
t Erlangen-Nu
¨
rnberg, Staudtstrasse 7, D-91058 Erlangen, Germany
共Received 28 February 2002; published 3 June 2002兲
In the covariant description of confinement, one expects the ghost correlations to be infrared enhanced.
Assuming ghost dominance, the long-range behavior of gluon and ghost correlations in Landau gauge QCD is
determined by one exponent
. The gluon propagator is infrared finite 共vanishing兲 for
⫽ 1/2 (
⬎ 1/2) which
is still under debate. Here, we study the critical exponent and coupling for the infrared conformal behavior
from the asymptotic form of the solutions to the Dyson-Schwinger equations in an ultraviolet finite expansion
scheme. The value for
is directly related to the ghost-gluon vertex. Assuming that it is regular in the infrared,
one obtains
⯝0.595. This value maximizes the critical coupling
␣
c
(
), yielding
␣
c
max
⯝(4
/N
c
)0.709
⬇2.97 for N
c
⫽ 3. For larger
the vertex acquires an infrared singularity in the gluon momentum; smaller ones
imply infrared singular ghost legs. Variations in
␣
c
remain within 5% from
⫽ 0.5 to 0.7. Above this range,
␣
c
decreases more rapidly with
␣
c
→0
⫹
as
→1
⫺
which sets the upper bound on
.
DOI: 10.1103/PhysRevD.65.125006 PACS number共s兲: 11.10.Gh, 11.10.Jj, 12.38.Aw, 12.38.Lg
I. INTRODUCTION
In gauge theories without Higgs mechanism, particles car-
rying the global charges of the gauge group cannot strictly be
localized. Localized physical states are necessarily neutral in
QED and colorless in QCD. The extension to all gauge in-
variant and thus physical states is possible only with a mass
gap in the physical world. Then, color-electric charge super-
selection sectors do not arise in QCD and one concludes
confinement.
The necessary conditions for this were formulated more
than 20 years ago. In the next section we briefly recall these
conditions and how they constrain the infrared behavior of
ghost and gluon propagators in the Landau gauge QCD.
Based on linear-covariant gauges, their derivation may not
fully be divorced from perturbation theory. Their essence is
quite generic and summarized in the Kugo-Ojima criterion
which should apply in one way or another, whenever some
form of Becchi-Rouet-Stora 共BRS兲 cohomology construction
does for gauge theories. One way towards a nonperturbative
definition of the Landau gauge is provided via stochastic
quantization for which the full five-dimensional BRS ma-
chinery is in the garage. The time-independent diffusion
equation of this formulation is closely related to the Dyson-
Schwinger equations 共DSEs兲 in four dimensions as we de-
scribe next. Some of the necessary extensions, which have
already been implemented in previous DSE studies of infra-
red exponents for other reasons, imply the Kugo-Ojima cri-
terion. We summarize these studies and how they are con-
firmed qualitatively in this way, at the end of the
Introduction. These various issues related to our study are
collected in Secs. I A–I D to supply additional background
information.
In Sec. II, we set up the DSE structures relevant for our
present study. We summarize the general properties of the
ghost-gluon vertex, most importantly its nonrenormalization
and ghost-antighost symmetry in the Landau gauge, which
will be essential for infrared critical exponents and coupling
later. We then present the ultraviolet subtraction procedure
with the special care necessary to make sure that it does not
artificially affect the infrared. Some confusion arose recently
concerning the relation between asymptotic infrared expan-
sions and the renormalization group which we first clarify in
Sec. III. We then review the nonperturbative definition of the
running coupling that is based on the nonrenormalization of
the ghost-gluon vertex in the Landau gauge, and show that in
four dimensions it approaches a constant
␣
c
in the infrared
whenever this vertex has an asymptotic conformal behavior
also. As a by-product of the vertex nonrenormalization, the
infrared behavior of both propagators thereby results to be
determined by one unique exponent
in any given dimen-
sion. The general machinery to determine the infrared critical
exponent and coupling is outlined in Sec. IV. There, we also
discuss the results with an additional regularity assumption
on the vertex in the infrared, which in four dimensions leads
to the values
⬇0.595 and
␣
c
⬅
␣
c
max
⯝(4
/N
c
)0.709
⬇2.97 for N
c
⫽ 3. We furthermore discuss the infrared trans-
versality of the vertex and show how this resolves an appar-
ent contradiction with a previous study.
We then discuss more general vertices involving an addi-
tional exponent which controls singularities in its external
momenta to discuss bounds on
␣
c
and
. Thereby we will
find that values of
smaller than that for the regular vertex
imply infrared divergences in ghost legs, whereas larger ones
lead to an infrared divergence of the vertex in the gluon
momentum. While the latter can only come together with an
infrared vanishing gluon propagator, which will always over-
compensate this divergence, the former add to the infrared
enhancement of ghost exchanges. In particular, this would
have to happen for an infrared finite gluon propagator 共with
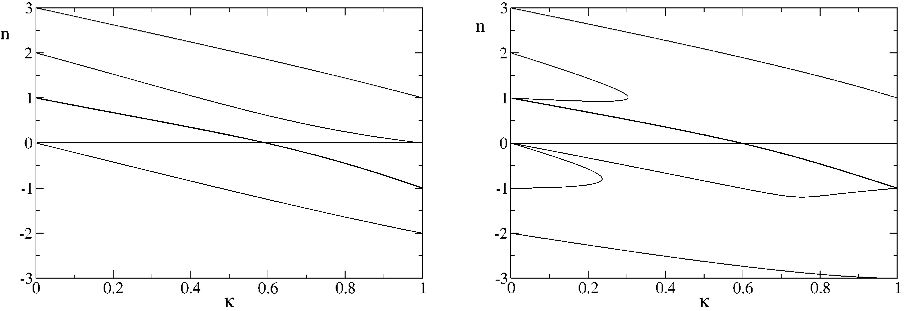
⫽ 0.5) as presently favored by lattice simulations.
Our summary and conclusions are given in Sec. V, and we
include two appendixes which may provide the interested
reader with some more technical details.
A. The Kugo-Ojima confinement criterion
Within the framework of BRS algebra, completeness of
the nilpotent BRS-charge Q
B
, the generator of the BRS
*
Now at Instituto de Fı
´
sica Corpuscular, Edificio Institutos de
Paterna, Apartado 22085, CP 46071, Valencia, Spain.
†
Electronic address: smekal@theorie3.physik.uni-erlangen.de
PHYSICAL REVIEW D, VOLUME 65, 125006
0556-2821/2002/65共12兲/125006共22兲/$20.00 ©2002 The American Physical Society65 125006-1

transformations, in a state space V of indefinite metric is
assumed. The semidefinite physical subspace V
phys
⫽ Ker Q
B
is defined on the basis of this algebra by those states which
are annihilated by the BRS charge Q
B
. Since Q
B
2
⫽ 0, this
subspace contains the space Im Q
B
of so-called daughter
states which are images of others, their parent states in V.A
physical Hilbert space is then obtained as 共the completion of兲
the covariant space of equivalence classes Ker Q
B
/ImQ
B
,
the BRS-cohomology of states in the kernel modulo those in
the image of Q
B
, which is isomorphic to the space V
s
of
BRS singlets. It is easy to see that the image is furthermore
contained in the orthogonal complement of the kernel 共given
completeness they are identical兲. It follows that states in
Im Q
B
do not contribute to the inner product in V
phys
.
Completeness is thereby important in the proof of positiv-
ity for physical states 关1,2兴, because it assures the absence of
metric partners of BRS singlets, so-called ‘‘singlet pairs.’’
With completeness, all states in V are either BRS singlets in
V
s
or belong to so-called quartets which are metric-partner
pairs of BRS-doublets 共of parent with daughter states兲; and
this then exhausts all possibilities. The generalization of the
Gupta-Bleuler condition on physical states, Q
B
兩
典
⫽ 0in
V
phys
, eliminates half of these metric partners leaving un-
paired states of zero norm which do not contribute to any
observable. This essentially is the quartet mechanism: Just as
in QED, one such quartet, the elementary quartet, is formed
by the massless asymptotic states of longitudinal and time-
like gluons together with ghosts and antighosts which are
thus all unobservable. In contrast to QED, however, one ex-
pects the quartet mechanism also to apply to transverse gluon
and quark states, as far as they exist asymptotically. A viola-
tion of positivity for such states then entails that they have to
be unobservable also. Increasing evidence for this has been
seen in the transverse gluon correlations over the last years
关3兴.
But that is only one aspect of confinement in this descrip-
tion. In particular, asymptotic transverse gluon and quark
states may or may not exist in the indefinite metric space V.
If either of them do, and the Kugo-Ojima criterion is realized
共see below兲, they belong to unobservable quartets. Then, the
BRS transformations of their asymptotic fields entail that
they form these quartets together with ghost-gluon and/or
ghost-quark bound states, respectively 关2兴. It is furthermore
crucial for confinement, however, to have a mass gap in
transverse gluon correlations. The massless transverse gluon
states of perturbation theory must not exist even though they
would belong to quartets due to color antiscreening and su-
perconvergence in QCD for less than ten quark flavors
关4,5,3兴.
Confinement depends on the realization of the unfixed
global gauge symmetries. The identification of gauge-
invariant physical states, which are BRS singlets, with color
singlets is possible only if the charge of global gauge trans-
formations is BRS exact and unbroken. The sufficient con-
ditions for this are provided by the Kugo-Ojima criterion:
Considering the globally conserved current
J
a
⫽
F
a
⫹
兵
Q
B
,D
ab
c
¯
b
其
共
with
J
a
⫽ 0
兲
, 共1兲
one realizes that the first of its two terms corresponds to a
coboundary with respect to the space-time exterior derivative
while the second term is a BRS coboundary. Denoting their
charges by G
a
and N
a
, respectively,
Q
a
⫽
冕
d
3
x
共
i
F
0i
a
⫹
兵
Q
B
,D
0
ab
c
¯
b
其
兲
⫽ G
a
⫹ N
a
. 共2兲
For the first term herein there are only two options, it is
either ill-defined due to massless states in the spectrum of
F
a
, or else it vanishes.
In QED massless photon states contribute to the ana-
logues of both currents in Eq. 共1兲, and both charges on the
right-hand side 共rhs兲 in Eq. 共2兲 are separately ill-defined. One
can employ an arbitrariness in the definition of the generator
of the global gauge transformations 共2兲, however, to multiply
the first term by a suitable constant so chosen that these
massless contributions cancel. In this way one obtains a
well-defined and unbroken global gauge charge which re-
places the naive definition in Eq. 共2兲 above 关6兴. Roughly
speaking, there are two independent structures in the globally
conserved gauge currents in QED which both contain mass-
less photon contributions. These can be combined to yield
one well-defined charge as the generator of global gauge
transformations leaving any other combination spontane-
ously broken, such as the displacement symmetry which led
to the identification of the photon with the massless Gold-
stone boson of its spontaneous breaking 关2,7兴.
If
F
a
contains no massless discrete spectrum on the
other hand, i.e., if there is no massless particle pole in the
Fourier transform of transverse gluon correlations, then G
a
⬅0. In particular, this is the case for channels containing
massive vector fields in theories with the Higgs mechanism,
and it is expected to be also the case in any color channel for
QCD with confinement for which it actually represents one
of the two conditions formulated by Kugo and Ojima. In
both these situations one first has equally, however,
Q
a
⫽ N
a
⫽
再
Q
B
,
冕
d
3
xD
0
ab
c
¯
b
冎
, 共3兲
which is BRS exact. The second of the two conditions for
confinement is that this charge be well-defined in the whole
of the indefinite metric space V. Together these conditions
are sufficient to establish that all BRS-singlet physical states
are also color singlets, and that all colored states are thus
subject to the quartet mechanism. The second condition
thereby provides the essential difference between the Higgs
mechanism and confinement. The operator D
ab
c
¯
b
determin-
ing the charge N
a
will in general contain a massless contri-
bution from the elementary quartet due to the asymptotic
field
␥
¯
a
(x) in the antighost field, c
¯
a
→
x
0
→⫾⬁
␥
¯
a
⫹ ••• 共in the
weak asymptotic limit兲,
D
ab
c
¯
b
→
x
0
→⫾⬁
共
␦
ab
⫹ u
ab
兲
␥
¯
b
共
x
兲
⫹ •••. 共4兲
Here, the dynamical parameters u
ab
determine the contribu-
tion of the massless asymptotic state to the composite field
CHRISTOPH LERCHE AND LORENZ VON SMEKAL PHYSICAL REVIEW D 65 125006
125006-2

gf
abc
A
c
c
¯
b
→
x
0
→⫾⬁
u
ab
␥
¯
b
⫹ •••. These parameters can be
obtained in the limit p
2
→0 from the Euclidean correlation
functions of this composite field, e.g.,
冕
d
4
xe
ip(x⫺ y)
具
D
ae
c
e
共
x
兲
gf
bcd
A
d
共
y
兲
c
¯
c
共
y
兲
典
⬅
冉
␦
⫺
p
p
p
2
冊
u
ab
共
p
2
兲
. 共5兲
The theorem by Kugo and Ojima asserts that all Q
a
⫽ N
a
are
well-defined in the whole of V 共and do not suffer from spon-
taneous breakdown兲, if and only if
u
ab
⬅u
ab
共
0
兲
⫽
!
⫺
␦
ab
. 共6兲
Then, the massless states from the elementary quartet do not
contribute to the spectrum of the current in N
a
, and the
equivalence between physical BRS-singlet states and color
singlets is established 关1,2,6兴.
In contrast, if det(1⫹ u)⫽0, the global gauge symmetry
generated by the charges Q
a
in Eq. 共2兲 is spontaneously bro-
ken in each channel in which the gauge potential contains an
asymptotic massive vector field 关1,2兴. While this massive
vector state results to be a BRS singlet, the massless Gold-
stone boson states which usually occur in some components
of the Higgs field replace the third component of the vector
field in the elementary quartet and are thus unphysical. Since
the broken charges are BRS exact, this hidden symmetry
breaking is not directly observable in the physical Hilbert
space.
The different scenarios are classified according to the re-
alization of the global gauge symmetry on the whole of the
indefinite metric space of covariant gauge theories. If it is
unbroken, as in QED and QCD, the first condition is crucial
for confinement. Namely, it is then necessary to have a mass
gap in the transverse gluon correlations, since otherwise one
could in principle have nonlocal physical 共BRS-singlet and
thus gauge-invariant兲 states with color, just as one has gauge-
invariant charged states in QED 共e.g., the state of one elec-
tron alone in the world with its long-range Coulomb tail兲.
Indeed, with unbroken global gauge invariance, QED and
QCD have in common that any gauge invariant localized
state must be chargeless/colorless 关2兴. The question is the
extension to nonlocal states as approximated by local ones.
In QED this leads to the so-called charge superselection sec-
tors 关8兴, and nonlocal physical states with charge arise. If in
QCD, with unbroken global gauge symmetry and mass gap,
every gauge-invariant state can be approximated by gauge-
invariant localized ones 共which are colorless兲, one concludes
that every gauge-invariant 共BRS-singlet兲 state must also be a
color singlet.
B. Infrared dominance of ghosts in the Landau gauge
The 共second condition in the兲 Kugo-Ojima confinement
criterion, u⫽⫺1 leading to well-defined charges N
a
, can in
Landau gauge be shown by standard arguments employing
Dyson-Schwinger equations 共DSEs兲 and Slavnov-Taylor
identities 共STIs兲 to be equivalent to an infrared enhanced
ghost propagator 关6兴. In momentum space the nonperturba-
tive ghost propagator of Landau gauge QCD is related to the
form factor occurring in the correlations of Eq. 共5兲 as fol-
lows:
D
G
共
p
兲
⫽
⫺ 1
p
2
1
1⫹ u
共
p
2
兲
, with u
ab
共
p
2
兲
⫽
␦
ab
u
共
p
2
兲
.
共7兲
The Kugo-Ojima criterion, u(0)⫽⫺1, thus entails that the
Landau gauge ghost propagator should be more singular than
a massless particle pole in the infrared. Indeed, there is quite
compelling evidence for this exact infrared enhancement of
ghosts in the Landau gauge 关9兴. For lattice calculations of the
Landau gauge ghost propagator, see Refs. 关10–12兴. The
Kugo-Ojima confinement criterion was also tested on the
lattice directly 关13兴.
Lattice verifications of the positivity violations for trans-
verse gluon states by now have a long history 关14–19兴. Nu-
merical extractions of their indefinite spectral density from
lattice data are reported in 关20兴. As mentioned, however, this
follows from color antiscreening and superconvergence in
QCD already in perturbation theory 关4,5兴, and it is indepen-
dent of confinement.
Its remaining dynamical aspect resides in the cluster de-
composition property of local quantum field theory in this
formulation 关8,2兴. Within the indefinite inner product struc-
ture of covariant QCD it can be avoided for colored clusters,
only without mass gap in the full indefinite space V. In fact,
if the cluster decomposition property holds for a gauge-
invariant product of two 共almost local兲 fields, it can be
shown that both fields are gauge-invariant 共BRS-closed兲
themselves. With mass gap in the physical world, this then
eliminates the possibility of scattering a physical asymptotic
state into a color singlet consisting of widely separated col-
ored clusters 共the ‘‘behind-the-moon’’ problem兲关2兴.
The necessity for the absence of the massless particle pole
in
F
a
in the Kugo-Ojima criterion shows that the 共un-
physical兲 massless correlations to avoid the cluster decom-
position property are not the transverse gluon correlations.
An infrared suppressed propagator for the transverse gluons
in Landau gauge confirms this condition. This holds equally
well for the infrared vanishing propagator obtained from
DSEs 关21,23,22兴, and conjectured in the studies of the impli-
cations of the Gribov horizon 关24,25兴, as for the infrared
suppressed but possibly finite ones extracted from improved
lattice actions for quite large volumes 关26–28兴.
An infrared finite gluon propagator with qualitative simi-
larities in the transverse components appears to result also in
simulations using the Laplacian gauge 关29兴. Related to the
Landau gauge, this gauge fixing was proposed as an alterna-
tive for lattice studies in order to avoid Gribov copies 关30兴.
For a perturbative formulation see Ref. 关31兴. Due to intrinsic
nonlocalities, its renormalizability could not be demonstrated
so far. Deviations from the Landau gauge condition were
observed already at O(g
2
) in the bare coupling in Ref. 关32兴.
Moreover, the gluon propagator was seen to develop a large
longitudinal component in the nonperturbative regime 关29兴.
INFRARED EXPONENT FOR GLUON AND GHOST... PHYSICAL REVIEW D 65 125006
125006-3

In fact, compared to the transverse correlations, it seems to
provide the dominant component in the infrared, and it might
in the end play a role analogous to that of the infrared en-
hanced ghost correlations in the Landau gauge. However, the
precise relation with Landau gauge still seems somewhat un-
clear. It is certainly encouraging nevertheless to first of all
verify that no massless states contribute to the transverse
gluon correlations of the Laplacian gauge either.
C. Nonperturbative Landau gauge
A problem mentioned repeatedly already, which is left in
the dark in the description of confinement within the covari-
ant operator formulation presented so far, is the possible in-
fluence of Gribov copies 关24兴.
Recently, renewed interest in stochastic quantization arose
because it provides ways of gauge fixing in the presence of
Gribov copies, at least in principle 关33,34兴. The relation to
Dyson-Schwinger equations is provided by a time-
independent version of the diffusion equation in this ap-
proach in which gauge-fixing is replaced by a globally re-
storing drift-force tangent to gauge orbits in order to prevent
the probability distribution from drifting off along gauge or-
bit directions.
In particular, in the limit of the Landau gauge, it is the
conservative part of this drift-force, the derivative with re-
spect to transverse gluon-field components of the Faddeev-
Popov action, which leads to the standard Dyson-Schwinger
equations as clarified by Zwanziger 关35兴. He furthermore
points out that these equations are formally unchanged if
Gribov’s original suggestion to restrict the Faddeev-Popov
measure to what has become known as the interior of the first
Gribov horizon is implemented. This is simply because the
Faddeev-Popov measure vanishes there, and thus no bound-
ary terms are introduced in the derivation of Dyson-
Schwinger equations 共DSEs兲 by this additional restriction.
Phrased otherwise, it still provides a measure such that the
expectation values of total derivatives with respect to the
fields vanish, which is all we need to formally derive the
same Dyson-Schwinger equations as those without restric-
tion.
In the stochastic formulation this restriction arises natu-
rally because the probability distribution gets concentrated
on the 共first兲 Gribov region as the Landau gauge is ap-
proached. Therefore there should be no problem of principle
with the existence of Gribov copies in the standard DSEs.
However, the distribution of the probability measure among
the gauge orbits might be affected by neglecting 共the non-
conservative兲 part of the drift force. Ways to overcome this
approximation are currently being investigated. Moreover,
providing for a correct counting of gauge copies inside the
Gribov region, the full stochastic equation will allow com-
parison with results from Monte Carlo simulations using lat-
tice implementations of the Landau gauge in a much more
direct and reliable way. In particular, this should be the case
for the lattice analog of the stochastic gauge fixing used in
simulations such as those of Refs. 关16–18兴.
Here, we restrict ourselves to the standard Landau gauge
DSEs which are best justified nonperturbatively from the sto-
chastic approach to be valid modulo the aforementioned ap-
proximation. For their solutions, on the other hand, restrict-
ing the support of the Faddeev-Popov measure to the interior
of the Gribov region has the effect of additional boundary
conditions to select certain solutions from the set of all pos-
sible ones which might contain others as well. Consider two
invariant functions Z(k
2
) and G(k
2
) to parametrize the Lan-
dau gauge structure,
D
共
k
兲
⫽
Z
共
k
2
兲
k
2
冉
␦
⫺
k
k
k
2
冊
, D
G
共
k
兲
⫽⫺
G
共
k
2
兲
k
2
,
共8兲
in Euclidean momentum space of gluon and ghost propaga-
tor, respectively. Additionally when obtained as DSE solu-
tions, suitable boundary conditions have to be satisfied by
these functions. The following infrared bounds were derived
by Zwanziger for each of the two as properties of the propa-
gators from the restricted measure.
The observation that the ‘‘volume’’ of configuration space
in the infinite-dimensional 共thermodynamic兲 limit is con-
tained in its surface lead to the so-called horizon condition
which entails that the ghost propagator must be more singu-
lar than a massless particle pole in the infrared 关35–37兴,
lim
k
2
→0
G
⫺ 1
共
k
2
兲
⫽ 0. 共9兲
This condition is equivalent to the Kugo-Ojima criterion, u
⫽⫺1 for well-defined color charges in the Landau gauge,
cf., Eqs. 共6兲 and 共7兲 with G(k
2
)⫽ 1/
关
1⫹ u(k
2
)
兴
.
From the proximity of the Gribov horizon in infrared di-
rections Zwanziger furthermore concluded 关25兴 that
lim
k
2
→0
Z
共
k
2
兲
/k
2
⫽ 0. 共10兲
This removes the massless transverse gluon states of pertur-
bation theory as also required by the Kugo-Ojima criterion.
The infrared vanishing of the gluon propagator is a stronger
requirement than this, however. It currently remains an open
question why this has not been seen in Monte Carlo simula-
tions as yet. An infrared suppression of the gluon propagator
itself, rather than Z(k
2
), was observed for the Landau gauge
in 关38兴 and, more considerably, at large volumes in SU共2兲 in
the three-dimensional case 关39–41兴, as well as in Coulomb
gauge 关42兴. The three-dimensional results are interesting in
that the large distance gluon propagator measured there
seems incompatible with a massive behavior at low momenta
共that was noted also in 关18兴兲. At very large volumes, it even
becomes negative 关40,41兴. This is the same qualitative be-
havior as obtained for the one-dimensional Fourier transform
of the DSE results of 关22,23兴 at small values for the remain-
ing momentum components, cf., Fig. 4 of 关9兴 versus Fig. 2 of
关40兴 or Fig. 6 of 关41兴. Qualitatively, the different dimension-
ality should not matter much here. On the other hand, the
extrapolation of the zero momentum propagator in 关41兴 leads
to a finite result which, however, still decreases 共slowly兲 with
the volume. This suggests that the physical volumes may still
CHRISTOPH LERCHE AND LORENZ VON SMEKAL PHYSICAL REVIEW D 65 125006
125006-4