




read more





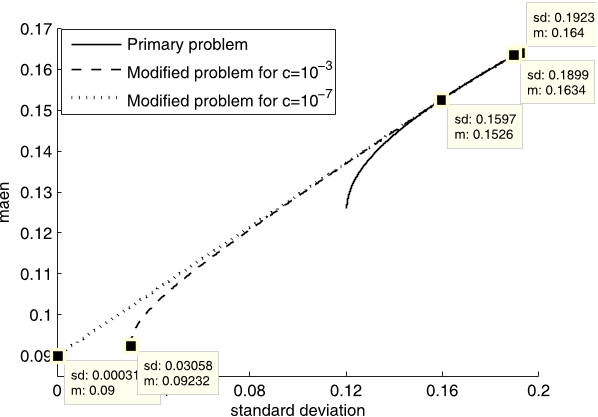


for values of c closed to zero, GMV portfolio acts like a totally riskless portfolio and that segment of the efficient frontier between the tangency portfolio and the GMV portfolio, tends to a straight line.
The major aim of the above works is to introduce methods which calculate the corner portfolios and the efficient frontier while significantly reducing computational time.
Also when portfolio contains a riskless asset with rf = 0.09 and borrowing is not allowed, the efficient frontier contains x11,x 2 1,x 3 1 and x 0 1 as the corner portfolios, where x01 corresponds to the totally riskless investment, i.e., (0,0.09), on the mean axis.
Note that, since x∗f = 0 for any ρ ≥ ρT and x∗f > 0 for any ρ < ρT , the tangency portfolio is a corner portfolio in the modified problem.
Since problems 1 and 2 have the same efficient frontiers on [ρ̂T , ρmax] and the efficient frontier of Problem 2 strictly dominates the efficient frontier of Problem 1 on [ρmin, ρ̂T ), the optimal CAL corresponding to Problem 2 which is tangent to the efficient frontier of the problem, is also tangent to the efficient frontier of Problem 1.
their model works directly with the optimal asset weights, instead of the Lagrangian multipliers, which is more clear to express, and also can employ other suitable PQP algorithms.
the efficient frontier of Problem 2 strictly dominates the efficient frontier of Problem 1 when ρ < ρ̂T .Corollary 3.3. ρmax = ρ̂max, where both of the problems 1 and 2 have the same optimal portfolio.
By the Karush-Kuhn-Tucker (K-K-T) conditions, X∗ = (x∗1, . . . , x∗n)′ is a (primal) solution or optimal portfolio of Problem 1, if and only if, there exist vectors λρ ∈ R, λb ∈ Rm and λd ∈ Rp such that:Σx∗ − λρR̄ − A′λb − C′λd = 0, R̄′x∗ = ρ,
As mentioned before, for example, the algorithm of Niedermayer and Niedermayer [13] can compute the efficient frontier of the standard problem with 2000 assets in less than a second.
Observe thatλ̂ρ̂T (ρ̂T − rf ) = x̂′Σx̂′ + cx∗f 2 = ρ̂T λ̂ρ̂T + b′λ̂b + d′λ̂d,where the last equation is obtained by adding the two first equations of (3.1) multiplied by x̂′ and x∗f , respectively.
the authors can locate the expected return of the tangency portfolio associated with Problem 1, which is also the tangency portfolio associated with Problem 2 (Cor. 3.4), by looking at the value of free variable in the solution of Problem 2.