
2.1 Depth Estimation of Frames in Image
Sequences Using Motion Occlusions
Guillem Palou, Philippe Salembier
Technical University of Catalonia (UPC), Dept. of Signal Theory and
Communications, Barcelona, SPAIN
{guillem.palou,philippe.salembier}@upc.edu
Abstract. This paper proposes a system to depth order regions of a
frame belonging to a monocular image sequence. For a given frame, re-
gions are ordered according to their relative depth using the previous
and following frames. The algorithm estimates occluded and disoccluded
pixels belonging to the central frame. Afterwards, a Binary Partition
Tree (BPT) is constructed to obtain a hierarchical, region based repre-
sentation of the image. The final depth partition is obtained by means
of energy minimization on the BPT. To achieve a global depth ordering
from local occlusion cues, a depth order graph is constructed and used to
eliminate contradictory local cues. Results of the system are evaluated
and compared with state of the art figure/ground labeling systems on
several datasets, showing promising results.
1 Introduction
Depth perception in human vision emerges from several depth cues. Normally,
humans estimate depth accurately making use of both eyes, inferring (subcon-
sciously) disparity between two views. However, when only one point of view is
available, it is also possible to estimate the scene structure to some extent. This
is done by the so called monocular depth cues. In static images, T-junctions or
convexity cues may be detected in specific image areas and provide depth order
information. If a temporal dimension is introduced, motion information can also
be used to get depth information. Occlusion of moving objects, size changes or
motion parallax are used in the human brain to structure the scene [1].
Nowadays, a strong research activity is focusing on depth maps generation,
mainly motivated by the film industry. However, most of the published ap-
proaches make use of two (or more) points of view to compute the disparity
as it offers a reliable cue for depth estimation [2]. Disparity needs at least two
images captured at the same time instant but, sometimes, this requirement can-
not be fulfilled. For example, current handheld cameras have only one objective.
Moreover, a large amount of material has already been acquired as monocular
sequences and needs to be converted. In such cases, depth perception should be
inferred only through monocular cues. Although monocular cues are less reliable
than stereo cues, humans can do this task with ease.

2 Depth Estimation of Frames Using Motion Occlusions
I
t−1
I
t
I
t+1
Optical flow &
(dis)occluded points
estimation
BPT
construction
Occlusion
relations
estimation
Pruning
Depth ordering
2.1D Map
Fig. 1. Scheme of the proposed system. From three consecutive frames of a
sequence (green blocks), a 2.1D map is estimated (red block)
The 2.1D model is an intermediate state between 2D images and full/absolute
3D maps, representing the image as a partition with its regions ordered by its
relative depth. State of the art depth ordering systems on monocular sequences
focus on the extraction of foreground regions from the background. Although this
may be appropriate for some applications, more information can be extracted
from an image sequence. The approach in [3] provides a pseudo-depth estima-
tion to detect occlusion boundaries from optical flow. References [4, 5] estimate
a layered image representation of the scene. Whereas, references [6, 7] attempt to
retrieve a full depth map from a monocular image sequence, under some assump-
tions/restrictions about the scene structure which may not be fulfilled in typical
sequences. The work [8] assigns figure/ground (f/g) labels to detected occlusion
boundaries. f/g labeling provides a quantitative measure of depth ordering, as it
assigns a local depth gradient at each occlusion boundary. Although f/g labeling
is an interesting field of study, it does not offer a dense depth representation.
A good monocular cue to determine a 2.1D map of the scene is motion occlu-
sion. When objects move, background regions (dis)appear, creating occlusions.
Humans use these occlusions to detect the relative depth between scene regions.
The proposed work assesses the performance of these cues in a fully automated
system. To this end, the process is divided as shown in Figure 1 and presented
as follows. First, the optical flow is used in Section 2 to introduce motion infor-
mation for the BPT [9] construction and in Section 3 to estimate (dis)occluded
points. Next, to find both occlusion relations and a partition of the current frame,
the energy minimization technique described in Section 4 is used. Lastly, the re-
gions of this partition are ordered, generating a 2.1D map. Results compared
with [8] are exposed in Section 5.
2 Optical Flow and Image Representation
As shown in Figure 2, to determine the depth order of frame I
t
, the previous
I
t−1
and following I
t+1
frames are used. Forward w
t−1,t
, w
t,t+1
and backward

Depth Estimation of Frames Using Motion Occlusions 3
w
t−1,t
w
t,t−1
w
t,t+1
w
t+1,t
Fig. 2. Left: color code used to represent optical flow values. Three consecutive
frames are presented in the top row, I
t−1
,I
t
in red and I
t+1
. In the bottom row,
from left to right, the w
t−1,t
,w
t,t−1
,w
t,t+1
,w
t+1,t
flows are shown.
flows w
t,t−1
, w
t+1,t
can be estimated using [10]. For two given temporal indices
a, b, the optical flow vector w
a,b
maps each pixel of I
a
to one pixel in I
b
.
Once the optical flows are computed, a BPT is built [11]. The BPT begins
with an initial partition (here a partition where each pixel forms a region).
Iteratively, the two most similar neighboring regions according to a predefined
distance are merged and the process is repeated until only one region is left. The
BPT describes a set of regions organized in a tree structure and this hierarchical
structure represents the inclusion relationship between regions. Although the
construction process is an active field of study, it is not the main purpose of this
paper and we chose the distance defined in [11] to build the BPT: the region
distance is defined using color, area, shape and motion information.
3 Motion Occlusions from Optical Flow
When only one point of view is available, humans take profit of monocular depth
cues to retrieve the scene structure: motion parallax and motion occlusions.
Motion parallax assumes still scenes, and it is able to retrieve the absolute depth.
Occlusions may work in dynamic scenes but only offer insights about relative
depth. Since motion occlusions appear in more situations and do not make any
assumptions, they are selected here. Motion occlusions can be detected with
several approaches [12, 13]. In this work, however, a different approach is followed
as it gave better results in practice.
Using three frames I
t−1
, I
t
, I
t+1
, it is possible to detect pixels becoming oc-
cluded from I
t
to I
t+1
and pixels becoming visible (disoccluded) from I
t−1
to I
t
.
To detect motion occlusions, the optical flow between an image pair (I
t
, I
q
) is
used with q = t ± 1. To obtain occluded pixels q = t + 1, while disoccluded are
obtained when q = t − 1.
Flow estimation attempts to find a matching for each pixel between two
frames. If a pixel is visible in both frames, the flow estimation is likely to find
the true matching. If, however, the pixel becomes (dis)occluded, the matching

4 Depth Estimation of Frames Using Motion Occlusions
will not be against its true peer. In the case of occlusion, two pixels p
a
and p
b
in I
t
will be matched with the same pixel p
m
in frame I
q
:
p
a
+ w
t,q
(p
a
) = p
b
+ w
t,q
(p
b
) = p
m
(1)
Equation (1) implicitly tells that either p
a
or p
b
is occluded. It is likely that the
non occluded pixel neighborhood is highly correlated in both frames. Therefore,
to decide which one is the occluded pixel, a patch distance is computed:
D(p
x
, p
m
) =
X
d∈Γ
(I
q
(p
m
+ d) − I
t
(p
x
+ d))
2
(2)
with p
x
= p
a
or p
b
. The pixel with maximum D(p
x
, p
m
) value is decided to be
the occluded pixel. The neighborhood Γ is a 5 × 5 square window centered at
p
x
but results are similar with windows of size 3 × 3 or 7 × 7.
Occluded and disoccluded pixels may be useful to some extent (e.g. to im-
prove optical flow estimation, [12]). To retrieve a 2.1D map, an (dis)occluded-
(dis)occluding relation is needed to create a depth order. (Dis)occluding pixels
are pixels in I
t
that will be in front of their (dis)occluded peer in I
q
. There-
fore, using these relations it is possible to order different regions in the frame
according to depth. In the proposed system, occlusion relations estimation is
postponed until the BPT representation is available, see Section 4.1. The rea-
son to do so is because raw estimated optical flows are not reliable in occluded
points. Nevertheless, with the knowledge of region information it is possible to
fit optical flow models to regions and provide confident optical flow values even
for (dis)occluded points.
4 Depth Order Retrieval
Once the optical flow is estimated and the BPT is constructed, the last step of
the system is to retrieve a suitable partition to depth order its regions. There are
many ways to obtain a partition from a hierarchical representation [14, 15, 9]. In
this work an energy minimization strategy is proposed. The complete process
comprises two energy minimization steps to find the final partition. Since raw
optical flows are not reliable at (dis)occluded points, a first step allows us to
find a partition P
f
where an optical flow model is fitted in each region. When
the occlusion relations are estimated, the second step finds a second partition P
d
attempting to maintain occluded-occluding pairs in different regions. The final
stage of the system relates regions in P
d
according to their relative depth.
Obtaining P
f
and P
d
is performed using the same energy minimization al-
gorithm. For this reason, the general algorithm is presented first in Section 4.1
and then it is particularized for each step in the following subsections.
4.1 General Energy Minimization on BPTs
A partition P, can be represented by a vector x of binary variables x
i
= {0, 1}
with i = 1..N , one for each region R
i
forming the BPT. If x
i
= 1, R
i
is in the

Depth Estimation of Frames Using Motion Occlusions 5
Algorithm 1 Optimal Partition Selection
function OptimalSubTree(Region R
i
)
R
l
, R
r
← (LeftChild(R
i
),RightChild(R
i
))
(c
i
, o
i
) ← (E
r
(R
i
), R
i
)
(o
l
, c
l
) ← OptimalSubTree(R
l
)
(o
r
, c
r
) ← OptimalSubTree(R
r
)
if c
i
< c
r
+ c
l
then
OptimalSubTree(R
i
) ← (o
i
, c
i
)
else
OptimalSubTree(R
i
) ← (o
l
S
o
r
, c
l
+ c
r
)
end if
end function
partition, otherwise x
i
= 0. Although there are a total of 2
N
possible vectors,
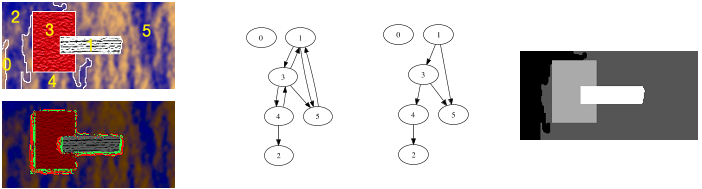
only a reduced subset may represent a partition, as shown in Figure 3. A given
vector x is a valid vector if one, and only one, region in every BPT branch has
x
i
= 1. A branch is the sequence of regions from a leaf to the root of the tree.
Intuitively speaking, if a region R
i
is forming the partition P (x
i
= 1), no other
region R
j
enclosed or enclosing R
i
may have x
j
= 1. This can be expressed as a
linear constraint A on the vector x. A is provided for the case in Figure 3:
Ax = 1
1 0 0 0 1 0 1
0 1 0 0 1 0 1
0 0 1 0 0 1 1
0 0 0 1 0 1 1
x = 1 (3)
Where 1 is a vector containing all ones. The proposed optimization scheme
finds a partition that minimizes energy functions of the type:
x
∗
= arg min
x
E(x) = arg min
x
X
R
i
∈BP T
E
r
(R
i
)x
i
(4)
s.t. Ax = 1 x
i
= {0, 1} (5)
where E
r
(R
i
) is a function that depends only of the internal characteristics of
the region (mean color or shape, for example). If that is the case, Algorithm 1
uses dynamic programming (Viterbi like) to find the optimal x
∗
.
Fitting the flows and finding occlusion relations As stated in Section 3,
the algorithm [10] does not provide reliable flow values at (dis)occluded points.
Therefore, to be able to determine consistent occlusion relations, the flow in
non-occluded areas is extrapolated to these points by finding a partition P
f
and
estimating a parametric projective model [16] in each region. The set of regions
that best fits to these models is computed using Algorithm 1 with E
r
(R
i
):
E
r
(R
i
) =
X
q=t±1
X
x,y∈R
i
w
t,q
(x, y) −
e
w
t,q
R
i
(x, y)
+ λ
f
(6)

![Table 1. Our method vs. [8] on the percentage of correct f/g assignments.](/figures/table-1-our-method-vs-8-on-the-percentage-of-correct-f-g-2vac4qn6.png)


