3D Estimation and Visualization of Motion in a
Multicamera Network for Sports
Anil Kumar, P. Shashidhar Chavan, Sharatchandra V.K
and Sumam David
National Institute of Technology Karnataka,
Karnataka, India
Email: {anil3487, shashi3494, sharatkashimath}@gmail.com
sumam@ieee.org
Philip Kelly and Noel E. O’Connor
CLARITY: Centre for Sensor Web Technologies,
Dublin City University,
Dublin 9, Ireland
Email: {philip.kelly, noel.oconnor}@dcu.ie
Abstract—In this work, we develop image processing and
computer vision techniques for visually tracking a tennis ball, in
3D, on a court instrumented with multiple low-cost IP cameras.
The technique first extracts 2D ball track data from each camera
view, using object tracking methods. Next, an automatic feature-
based video synchronization method is applied. This technique
uses both the extracted 2D ball information from two or more
camera views, plus camera calibration information. Then, in
order to find 3D trajectory, the temporal 3D locations of the ball
is estimated using triangulation of correspondent 2D locations
obtained from automatically synchronized videos. Furthermore,
we also incorporate a physics-based trajectory model into the
system to improve the continuity of the tracked 3D ball during
times when no two cameras have overlapping views of the ball
location. The resultant 3D ball tracks are then visualized in
a virtual 3D graphical environment. Finally, we quantify the
accuracy of our system in terms of reprojection error.
I. INTRODUCTION
In professional sports we are familiar with high-end camera
technology being used to enhance the viewer experience above
and beyond a traditional broadcast. High profile examples
include the Hawk-Eye Officiating System as used in tennis,
snooker and cricket. Whilst extremely valuable to the viewing
experience, such technologies are only feasible for high profile
professional sports. Sports video analysis has also been exten-
sively used by coaches for the effective training of athletes.
Presently, there are several commercial technological solutions
for sports video analysis. However, these systems, again, tend
to be expensive to purchase and run.
Advances in camera technology, coupled with falling prices
means that reasonable quality visual capture is now within
reach of most local and amateur sporting and leisure organi-
zations. Thus it becomes feasible for every field sports club,
whether tennis, soccer, cricket or hockey, to install their own
camera network at their local ground. By enabling sports video
analysis with low cost camera networks, many local amateur
clubs and sports institutions will be able to make use of these
types of technologies. In these cases, the motivation is usually
not for broadcast purposes, but rather for the technology to act
as a video referee or adjudicator, and also to facilitate coaches
and mentors to provide better feedback to athletes based on
recorded competitive training matches, training drills or any
prescribed set of activities.
In this work, we focus on tracking a tennis ball in 3D space
during a tennis match using the videos obtained from low-
cost camera network. Although the obtained 3D data could be
used for decision making purposes, as in Hawk-Eye, we focus
on its use as a low-cost tennis analysis system for coaching.
This 3D ball track data can be used for analysis purposes
such as determining the speed of the ball over the net (a
common tennis coach requirement), classification of type of
shots played by the players, or to index the video frames and
classify important events for coaching [1]. One of the main
problems from using low-cost camera networks is that the
cameras are typically no synchronization between sensors, as
such a need for automatic video synchronization algorithms
exists. In addition, the use of less expensive cameras also
lead to the distortion [2] in the videos acquired, hence camera
calibration of both camera intrinsics, as well as extrinsics, is
essential. In this work, we also introduce a physics based
model into our system, to predict the position of the ball
when there is a lack of overlapping data from different camera
views. Modeling of the ball trajectory is an essential part of
this system as it provides continuity of the tracked features,
leading to improvised tracking robustness.
The remainder of this paper is organized as follows: Section
II outlines previous work in the area. We give a high-level
overview of our system in section III. In this section, we
the subsequently describe the video analysis components that
underpin the ball tracking techniques. In addition, this section
provides details on physics based modeling that we incorpo-
rated and visualization framework developed using OpenGL.
Section IV provides quantitative experimental evaluation of
our system in terms of reprojection error, and graphical results
indicating the advantages of prediction. Finally, we give our
conclusions and directions for future work in section V.
II. RELATED WORK
The work of [1] illustrates how a low-cost camera network
could be effectively used for performance analysis if ball and
player tracks are known. Our work extend that described by
Aksay et. al.[3], where techniques for 2D ball tracking, feature
based automatic video synchronization and 3D estimation are
described. We utilize the above mentioned techniques and
improvise the overall quality of the system by developing our

Fig. 1. Camera locations around the court.
Fig. 2. Block diagram of the system.
own algorithm for prediction in case of missing points in the
trajectory. For this work. the dataset from the “3DLife ACM
Multimedia Grand Challenge 2010 Dataset ”[4] is utilized.
This dataset includes 9 video streams of a competitive singles
tennis match scenario from 9 IP cameras placed at different
positions around an entire tennis court – see Figure1. This
dataset also includes chessboard images and 3D locations of
some known objects in the scene for camera calibration.
III. ALGORITHMIC DESIGN
Figure 2 represents our system at a block level. We use
videos acquired from both sideview cameras and the overhead
camera in the dataset for 2D ball detection and tracking, as
explained in III-A. Camera calibration data is acquired for
each individual camera using the Matlab camera calibration
toolbox [5]. Once the tracking information from each of the
2D camera view was acquired, every cameras video stream is
synchronized with respect to overhead camera – see Section
III-B. Once synced, the 3D ball tracking is extended into 3D
space using the camera calibration information as explained
Section III-C. We then introduce a physics based trajectory
model, which is required to provide continuity in obtained
3D data ball tracks. The algorithmic description of trajectory
modeling is provided in Section III-D. Finally, we created a
virtual tennis court using OpenGL and visualized the motion
(a) (b) (c)
Fig. 3. Results of Object Tracking using frame differencing and thresholding;
(a) Original Frame; (b) Dilated Moving Pixels (c) Ball Blob.
of the ball, which is explained in detail in Section III-E.
A. 2D Ball Detection and Tracking
Object tracking techniques include frame differencing, op-
tical flow, mean-shift and various other methods. A simple
frame differencing and thresholding method would suffice in
the given context, since the data set provided has a static
background with the only moving objects being tennis ball
and players. In order to extract the ball trajectories, we begin
with detection of ball candidates for every video frame S(n).
We use method similar to the one described in [3]. All of
the moving parts of the frame that satisfy certain color and
size constraints are initially considered as ball candidates. We
detect moving parts by utilizing the luminance adjacent frames
difference. For the n
th
luminance frame, S
y
(n), we obtainthe
moving parts by thresholding the image, M (n), calculated as:
M(n) = abs[S
y
(n + 1) − S
y
(n)].abs[S
y
(n) − S
y
(n − 1)] (1)
where the . in the above equation represents element by
element multiplication.In this way, the real moving parts of
S(n) are heavily emphasised in M(n). Using 3 adjacent
frames to detect moving parts in the middle frame, as in
equation 1, is necessary step so that ambiguities in the location
of moving parts are avoided.
To eliminate the false candidates from the obtained loca-
tions, distance, colour and size constraints are applied. We
first eliminate false candiadates based on the colour infor-
mation. The blue, C
b
, and red, C
r
, channel values of the
tennis ball is inspected over diferent frames and for different
cameras. An empirical values of C
b
and C
r
is set and moving
pixels outside this range are eliminated. Next, we apply
morphological operations (dilation) to enhance the size of
the moving pixels, which otherwise, would be verydifficult to
discrimanate between different objects. Dilation will also come
into advantage in identifying the blobs correspondingto players
and tennis ball, as blobs corresponding to players will be much
larger compared to the blobs corresponding to balls. Hence,
by empirically setting a threshold value on the blob size,
largerblobs are removed. The final constraint considered when
eliminating false ball candidates is basedon distance between
tennis ball positions in two consecutive frames.A maximum
distance is set and any moving pixels outside this distance
areeliminated. This way, only one coordinate (corresponding
to center of mass of tennis ball) is extracted for each frame.
Figure 3(b) and (c) shows the results of the above discussed
techniques on an input frame.

Fig. 4. Plot of LM (∆) vs. Framedelay
B. 3D Estimation and Video Synchronization
Since the tennis videos in our data set are recorded at differ-
ent frame rates,there is no guarantee of the videos being started
at same time or that there will be no dropped frames through
each sequence. As such, there is need to synchronize these
videos before the 2D ball tracks from multiple cameras can be
used for 3D estimation. As such, we implemented the feature
based automatic video synchronization technique explained in
[3]. This method requires estimated 3D coordinate features
for each frame in order to know the de-synchronized timing.
Hence, its an inter-dependency problem where 3D coordinates
are required to synchronize the videos, and synchronized
videos are required to calculate accurate 3D coordinate. We
first calculate the 3D trajectories point-by-point using trian-
gulation [6] of two 2D trajectories from the two videos to be
synchronized. Then, the 3D trajectoriesare back-projected onto
one of the camera views. Assuming that the camera calibration
is accurate, back-projected 3D trajectories should be almost
identical to the 2D original camera trajectories when the time
shift used is close to the real de-synchronization of the videos.
However, due to issues such as non-ideal calibration data and
outlier 3D trajectories, the measure, LM(∆), suggested in [3]
is used to find out the best matching time shift ∆
max
.
LM(∆) =
L(∆)
D(∆)
, L(∆) = count(||or − bp|| < T
L
) (2)
D(∆) =
Σ||or − bp|| < T
L
L(∆)
(3)
where ||or −bp|| is the euclidean distance between the original
point and back projected point and ∆ is the tested time
shift. D(∆) is normalized euclidean distance between points,
calculated using only those points whose reprojected points
are within distance of some empirically set value of T
L
. The
required time shift is
∆
max
= arg max(LM(∆)) (4)
Figure 4 shows the plot of LM (∆) for different frame delays
in a test scenario. We choose the value of frame delay
that corresponds to the maximum value of LM(∆). In this
work, all the videos were synchronized with reference to
the overhead camera, since this camera has a field of view
covering the whole of the tennis court.
C. Robust 3D Tracking
A disadvantage of considering only two cameras is that
we dont get a continuous temporal 3D ball track stream due
to lack of availability of the synchronized 2D data in two
views through all the frames. To overcome this drawback, we
employed a robust 3D tracking method using3D coordinates
obtained from different camera pairs at different points in time.
We combine the tracking data from these multiple cameras to
calculate a more stable, robustand accurate 3D ball trajectory.
Let a 2D coordinate of the tennis ball at time instance, t, in
i
th
camera view be p
2D,i
= [x
i
(t), y
i
(t)]
T
. We calculate 3D
points using triangulation of the 2D points in each camera
(p
2D,i
) with the 2D point in theoverhead camera (the 9
t
h
camera) (p
2D,9
):
p
3D,i
= triangulate(p
2D,i
, p
2D,9
). (5)
The 3D points calculated at each time instance correspond
toone real-world 3D coordinate and ideally all of them should
be identical. However, due to several factors like camera cali-
bration errors, 2D tracker errors ortriangulation approximation,
each of the 3D points will tend to differ slightly, so some
formal technique for combining these multiple 3D points is
needed. in this work, we use a weighted averaging to find a
robust andaccurate 3D point p
3D
p
3D
=
P
i
w
i
∗ p
3D,i
P
i
w
i
(6)
where, w
i
is the measure for the level of accuracy of each
3D pointp
3D,i
. w
i
is calculated as the inverse Euclidean
distancebetween the original 2D point (p
2D,9
) and the back
projected 2D point (bp
2D,i
) on the 9
th
camera view. as shown
below.
w
i
=
1
d
i
=
1
||p
2D,9
, bp
2D,i
||
(7)
D. Physics Based Trajectory Modeling
Temporal prediction of the ball coordinates through times
when no 3D ball information is available is necessary because
to increase the continuity in the tracked features. This predic-
tion is achieved by considering the trajectory of the ball to be
a projectile. Projectiles are particles which are projected under
gravity through air, such as objects thrown by hand or shells
fired from a gun. Typically, mathematics describe projectiles
with both horizontal and vertical velocity components, and are
subject to a downward vertical acceleration (i.e. acceleration
due to gravity). To simplify the problem, few assumptions
have been made. Parameters like air resistance and ball spin,
which would require modification in the modeling, have been
neglected. We consider following kinematic equations of mo-
tion to predict the position of the ball in case of missing 3D
points:
v = u + at (8)
s = ut +
1
2
at
2
(9)
v
2
= u
2
+ 2as (10)
where v is the velocity at any time t, u is the initial velocity, a
is acceleration, and s is the distance traveled in time t. In our
problem, as air resistance and ball spin are not considered, only

Fig. 5. Visualization of ball trajectory at two different viewpoints.
the Z component of acceleration exists (-gravity), so the X and
Y components of acceleration are set to zero. We consider x,
y and z components of velocities separately and apply above
equations to predict position of the ball in case of missing
points in ball trajectory.
The coordinates are predicted using following steps: Say,
frames i to i + k require prediction
1) For the frame i with no 3D coordinate estimated, the
x,y,z components of velocities are found out using
tracked 3D points in frames i − 1 and i − 2.
2) Using this velocity information and equations of motion,
the 3D coordinate in the frame i is predicted.
3) Step 1 & 2 are carried out for all consecutive frames
(up to frame i + k).
4) Predicted points are retained only if the predicted point
in frame i + k is within some tolerable distance of the
estimated 3D coordinate in the frame i + k + 1.
E. Visualization Framework
If the developed algorithms have to be effectively used for
performance analysis by coaches or as a decision making
tool, a 3D graphical user interface (GUI) is essential, as the
visualisation makes the system more intuitive and appealing.
We have developed a GUI using OpenGL [7], one of the most
widely used and supported 2D and 3D graphics application
programming interface (API). It is hardware independent and
very much portable, hence it can be used wide across many
platforms. The frame work we developed is a virtual tennis
court, with an interface of selectingdifferent camera views and
zoom in features – see Figure 5.
IV. EXPERIMENTAL RESULTS
To evaluate our approach, we quantify the accuracy of our
system interms of reprojection error, which is defined as the
distance between the actual 2D pixel coordinates and the
reprojected pixel coordinates calculated using L1 Norm.
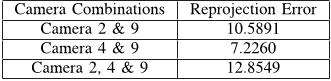
TABLE I
REPROJECTION ERRORS
Camera Combinations Reprojection Error
Camera 2 & 9 10.5891
Camera 4 & 9 7.2260
Camera 2, 4 & 9 12.8549
Table I shows the reprojection error obtained for different
combinations of cameras used for 3D tracking. As the number
of cameras considered for analysis increases, the number of
tracked points also increases, but at the cost of reprojection
error. Unfortunately, for the tracked points with inclusion of
Fig. 6. Continuity of tracked features for different conditions
(a)
(b)
Fig. 7. Reprojected trajectory (green) of the ball; (a) without prediction, and;
(b) with prediction
prediction model, the reprojection error can not be calculated
since we do not have ground truth data to compare with.
A graphical representation of the results obtained for various
techniques is shown in Figure 6. In this figure, time is on
the horizontal axis, and times at which the ball is tracked is
highlighted with a horizontal line, with times when the ball
track is lost represented by a gap. From this figure, we can
see that with increasing the number of cameras for tracking
the continuity in the tracked features also increases. The
bottom line represents continuity when trajectory modeling
is included. We can observe that some of the gaps are filled
after incorporating prediction in the system.
This advantage of incorporating trajectory modeling can
also be seen in Figure 7, where trajectories with and without
prediction are depicted. Notice how the tracked trajectory of
the ball (in green) is increased in (b) when compared to (a).
V. CONCLUSIONS AND FUTURE WORK
In this paper we presented algorithms associated with 2D
& 3D object tracking and video synchronization. We also
presented a basic, physics based modelling to increase the-
continuity of the tracked features. We believe that, though
the prediction model is very basic, it could be the first step
towardsdevelopment of a complex modelling system. In future
work, an accurate modelling of the ball trajectory could be
developed to ensure the continuity of the tracked features, by
considering realtime scenarios like ball spin and air resistance.
ACKNOWLEDGMENT
This work is supported by Science Foundation Ireland under grant
07/CE/I1147.

REFERENCES
[1] P. Kelly, J. Diego, P.-M. Agapito, C. O. Conaire, D. Connaghan, J. Kuk-
lyte, and N. E. O’Connor., “Performance analysis and visualisation in
tennis using a low-cost camera network,” in Multimedia Grand Challenge
Track at ACM Multimedia, 2010.
[2] G. Bradski and A. Kaehler, Learning OpenCV-Computer Vision with
OpenCV Library, M. Loukides, Ed. OReilly Publications, 2008.
[3] A. Aksay, V. Kitanovski, K. Vaiapury, E. Onasoglou, J. D. P. M. Agapito,
P. Daras, and E. Izquierdo., “Robust 3d tracking in tennis videos.” in
Engage Summer School, Sept. 2010.
[4] C. O. Conaire, P. Kelly, D. Connaghan, and N. E. O’Connor., “Tennis-
sense: A platform for extracting semantic information from multi-camera
tennis data,” in DSP 2009 - 16th International Conference on Digital
Signal Processing, 2009, pp. 1062–1067.
[5] J. Bouguet, “Camera calibration toolbox for matlab.” [Online]. Available:
http://www.vision.caltech.edu/bouguetj/
[6] Y. Morvan, “Acquisition, compression and rendering of depth and tex-
ture for multiview video,” Ph.D. dissertation, Eindhoven University of
Technology, Eindhoven, The Netherlands, 2009.
[7] K. Group, “Opengl overview.” [Online]. Available:
http://www.opengl.org/about/overview/