Ursinus College
Digital Commons @ Ursinus College
0&#*0'!/+",*-10#.!'#+!#!1)04
1 )'!0',+/
0&#*0'!/+",*-10#.!'#+!##-.0*#+0
A Distributed Greedy Algorithm for Constructing
Connected Dominating Sets in Wireless Sensor
Networks
Akshaye Dhawan
Ursinus College"&3+1./'+1/#"1
Nicholas A. Scoville
Ursinus College+/!,2'))#1./'+1/#"1
Michelle Tanco
Ursinus College*'0+!,1./'+1/#"1
,)),30&'/+"""'0',+)3,.(/0 &7-/"'%'0)!,**,+/1./'+1/#"1*0&!,*-$!
.0,$0&# +"#03,.(/,**,+/+"0&# 6#,.4+")%,.'0&*/,**,+/
Click here to let us know how access to this document benets you.
6'/,+$#.#+!#.,!##"'+%'/ .,1%&00,4,1$,.$.##+",-#+!!#// 40�&#*0'!/+",*-10#.!'#+!##-.0*#+00'%'0),**,+/
./'+1/,))#%#0&/ ##+!!#-0#"$,.'+!)1/',+'+0&#*0'!/+",*-10#.!'#+!#!1)041 )'!0',+/ 4+10&,.'5#""*'+'/0.0,.,$
'%'0),**,+/./'+1/,))#%#,.*,.#'+$,.*0',+-)#/#!,+0!0 -.,!(1./'+1/#"1
#!,**#+"#"'00',+
(/&4#&3+'!&#))#+!,'!&,)/!,2'))#'/0.' 10#".##"4)%,.'0&*$,.,+/0.1!0'+%,++#!0#",*'+0'+%#0/
'+'.#)#//#+/,.#03,.(/

A Distributed Greedy Algorithm for Constructing Connected
Dominating Sets in Wireless Sensor Networks
Akshaye Dhawan, Michelle Tanco and Nicholas Scoville
Department of Mathematics and Computer Science, Ursinus College, 610 E Main Street, Collegeville, PA, USA
{adhawan, mitanco, nscoville}@ursinus.edu
Keywords:
Wireless Sensor Networks, Dominating Sets, Distributed Algorithms
Abstract:
A Connected Dominating Set (CDS) of the graph representing a Wireless Sensor Network can be used as a
virtual backbone for routing in the network. Since sensor nodes are constrained by limited on-board batteries,
it is desirable to have a small CDS for the network. However, constructing a minimum size CDS has been
shown to be a NP-hard problem. In this paper we present a distributed greedy algorithm for constructing a
CDS that we call Greedy Connect. Our algorithm operates in two phases, first constructing a dominating
set and then connecting the nodes in this set. We evaluate our algorithm using simulations and compare it
to the two-hop K2 algorithm in the literature. Depending on the network topology, our algorithm generally
constructs a CDS that is up to 30% smaller in size than K2.
1 INTRODUCTION
Wireless Sensor Networks (WSNs) have attracted
considerable research interest in the past decade
(Iyengar and Brooks, 2004) (Akyildiz et al., 2002)
(Chong and Kumar, 2003). They have evolved from
research to deployment with many environmental, se-
curity, energy and other applications. WSNs consist
of a number of low-cost sensors scattered in a geo-
graphical area of interest and connected by a wire-
less RF interface. Sensors gather information about
the monitored area and send this information to gate-
way nodes known as sinks. Most common network
models consist of a distributed and localized control
with no central management. Each sensor serves as
both a data gathering source and a router, forward-
ing messages from other nodes. In order to keep their
cost low, the sensors are equipped with limited energy
(Feeney and Nilsson, 2001) (Feeney, 2001) and com-
putational resources. The energy supply is typically in
the form of a battery and once the battery exhausted,
the sensor is considered to be dead. A key approach
to solve the problem of data gathering and communi-
cation involves the construction of a connected domi-
nating set (CDS) that serves as a virtual backbone for
the network.
In this paper, we use a graph G = (V, E) to repre-
sent the wireless sensor network, where V is the set
of sensors in the network and an edge (u, v) ∈ E rep-
resent a link between two sensors u, v that are within
communicating distance of each other. We also as-
sume that all sensors are deployed on a 2-dimensional
plane and have a uniform transmission range. The re-
sulting graph is known as a Unit-Disk Graph (UDG)
(Clark et al., 1990) since the uniform transmission
range results in edges of equal (or unit) weight. We
also assume that the transmission range is at least
twice the sensing range since as shown in (Zhang and
Hou, 2005) a covered network is also connected if this
is true.
Given such a representation of a sensor network,
a dominating set (DS) of a graph G is a subset D ⊂ V
such that for all u ∈ V either u ∈ D or u is adjacent to a
node in D (i.e., (u, w) ∈ E for some w ∈ D). Nodes in
the dominating set D are referred to as dominators and
the remaining nodes in V − D are referred to as dom-
inatees. A Connected Dominating Set (CDS) is a set
that is dominating and induces a connected subgraph.
In other words, it is a set of nodes C ⊂ V such that the
nodes in C are both dominating and connected.
The construction of a CDS provides the network
with a virtual backbone over which routing, multicast
and broadcast can be performed since every node is
either in the backbone or has a neighbor in the back-
bone. Also, the construction of a CDS, allows the net-
work to adapt to changes in the topology since only
the nodes in the CDS need to be aware of routing
information. By being connected the backbone can
relay a message to either the destination directly (if
the destination is in the CDS) or through the domi-

nator of the destination. Since the nodes in the CDS
are actively draining their batteries by serving as re-
lay nodes for the network, it is desirable to construct
a minimum size CDS. However this has been shown
to be a NP-hard problem in (Clark et al., 1990). Much
attention has been given to centralized algorithms
based on the use of a maximal independent set (MIS)
to construct a CDS. The current best performance ra-
tio of 4.8 + ln5 was shown in (Li et al., 2005).
In this paper, we present a two-phase distributed
and localized greedy algorithm that first constructs a
dominating set (Phase 1) and then connects it (Phase
2). Our algorithm assumes that each sensor has a
unique identifier. The resulting CDS has been shown
to be significantly smaller in size to that of a compara-
ble distributed algorithm in the literature that we call
K2 (Dai and Wu, 2004).
The remainder of this paper is organized as fol-
lows in Section 2, we look at the literature on con-
struction of connected dominating sets. In Section 3
we explain our two phase algorithm. We look at a
simulation evaluation of our algorithm in Section 4.
Finally, we conclude in Section 5.
2 Related Work
In this section we briefly summarize related work in
this area. Considerable work has been done in the
development of both centralized and distributed algo-
rithms for CDS construction in the literature. Below
we focus mostly on distributed algorithms.
The applications of a connected dominating set
to routing in ad hoc networks were first outlined in
(Ephremides et al., 1987) where they presented the
idea of constructing a virtual backbone and its appli-
cation to routing. This paper led to several papers that
design approximation algorithms for this problem. A
coloring scheme similar to the one we use is a com-
mon theme in many of these papers with all nodes be-
ing white initially, with dominator’s being black and
dominatee’s being grey at the conclusion of these al-
gorithms.
(Guha and Khuller, 1998) presents a centralized
algorithm with a O(H∆) approximation factor where
∆ is the maximum degree and H is the harmonic func-
tion. In (Ruan et al., 2004) the authors present a 1-
phase greedy algorithm that has a performance ra-
tion of 2 + ln∆. (Funke et al., 2006) was one of the
first distributed algorithms to show an improved anal-
ysis of the relationship between the size of a maximal
independent set and a minimum CDS in a unit disk
graph, which yields better bounds for many other al-
gorithms. (Wan et al., 2002) presents a distributed al-
gorithm for CDS construction by constructing a span-
ning tree first and then labeling every node in the tree
as a dominator or dominatee. The Performance Ra-
tio for this algorithm was shown to be 8. In (Alzoubi
et al., 2002) the same authors noticed the difficulty
of maintaining a CDS and designed a localized 2-
phase algorithm that uses a Maximal Independent Set
but this algorithm has a PR of 192. (Li et al., 2005)
presents the best known PR of 4.8 + ln5 in a central-
ized algorithm. The algorithm is known as S-MIS and
uses a Steiner Tree to construct a CDS. In this algo-
rithm they build a Maximal Independent Set in Phase
1. Then in Phase 2, they employ a greedy algorithm
to construct a Steiner tree with minimal number of
Steiner nodes to connect the nodes in the MIS. They
mention that a distributed implementation is possible
but do not elaborate on this algorithm or its PR.
(Wu and Li, 1999) presents an earlier version of a
pruning algorithm that the authors refined into the K2
algorithm. Finally, we look at the K2 algorithm (Dai
and Wu, 2004) that we compare ourselves against.
The algorithm is a two phase algorithm which first
creates a connected dominating set and then reduces
the size of the set. In phase one, each sensor adds
itself to the dominating set if any two of its neigh-
bors are not neighbors. It is clear that if we start
with a connected graph we will get a connected dom-
inating set since any two non-connected sensors that
share a neighbor will be connected. However, this
set is likely to contain many more nodes than neces-
sary since the marking process was very simple. In
order to reduce the size of the set, the authors use a
k-reduction (where k is the number of hops the al-
gorithm is looking at) to remove unnecessary sensors
from the set. For each sensor in the dominating set we
consider every k-hop group of neighbors where each
member of the group is in the dominating set. If one
of these groups contains every neighbor of the origi-
nal sensor in its neighbor set, we remove the original
sensor from the dominating set. The dominating set
is still connected by the group of k neighbors. We
call this the K2 algorithm because we compare our-
selves against the 2-hop version of this algorithm. As
k increases, the size of the connected dominating set
decreases. However, the message and time complex-
ity increase since we have to check each size k group
of neighbors for each sensor. For the purposes of this
paper we let k = 2, since an algorithm cannot be lo-
calized and use a reasonable number of messages if it
requires more than 2-hops of information. This algo-
rithm has the benefit of the CDS being easy to main-
tain.

3 Greedy Connect Algorithm for
CDS construction
In this section we present our greedy, distributed al-
gorithm for constructing a connected dominating set.
The algorithm is a two-phase algorithm. In Phase 1,
we construct a dominating set and in Phase 2, we con-
nect the dominating set to form a connected dominat-
ing set. We begin by presenting Phase 1 - a greedy
approach to constructing a dominating set.
In this section, we will use a graph G = (V, E) to
represent the sensor network. We will also use the
notation N(u) to denote the one-hop neighbor set of
node u ∈ V . We also assume every sensor node to
have a unique identifier. The sensor nodes fields as
used in our algorithm are shown in Table 1.
Table 1: Fields for a given sensor node v
Field Meaning
v.COLOR The current color of the sensor
v.ID Unique identifier for the sensor
v.WhiteCount Number of white nodes in N(v)
3.1 Phase 1: Greedy construction of a
dominating set
Phase 1 uses node coloring to implement its greedy
approach. We summarize the meaning of the colors
in Table 2. Initially we start out with all nodes be-
ing colored white. The heuristic is greedy because
our criteria for adding nodes to the dominating set is
to pick the node that dominates the highest number
of non-dominated nodes. The color white represents
nodes that have not been dominated. When a node is
added to the dominating set, it is colored black and its
neighbors are colored grey to indicate that they have
been dominated.
Table 2: Node color assignments for Phase 1.
Color Meaning
White Undiscovered by the Dominating Set
Grey Dominated but has white neighbors
Black Dominated and has no white neighbors
In the first pass, every node every node exchanges
its white neighbor count with its neighbors. At this
point, the node with the highest white neighbor count
adds itself to the dominating set by changing its color
to black and changing the color of its white neighbors
to grey. Since this pass happens asynchronously, there
is a possibility (as shown by the example in Section
3.3) that some nodes have not yet been dominated.
The second pass looks at only those nodes that are
still white and essentially repeats the process to en-
sure that the set is dominating.
Require: ∀ v ∈ V v.COLOR ← WHITE
if v.COLOR ==WHITE then
*Initially every node will do this once*
Request the white neighbor count for every neigh-
bor u ∈ N(v)
if v.WhiteCount >= u.WhiteCount
∀u ∈ N(v) then
v.COLOR ← BLACK
for every neighbor u ∈ N(v) do
if u.COLOR == WHITE then
u.COLOR ←GREY
end if
end for
end if
end if
if v.COLOR==WHITE then
Request the white neighbor count for every neigh-
bor u ∈ N(v)
high← The node with the highest WhiteCount
high.COLOR ← BLACK
for every neighbor u ∈ N(high) do
if u.COLOR == WHITE then
u.COLOR ←GREY
end if
end for
end if
When the above algorithm concludes, we are left
with a dominating set that is possibly fragmented into
disconnected components. In Phase 2 we will connect
these components. The time complexity of this phase
is O(n∆), where ∆ is the maximum degree of a node in
V . This is because the first pass takes O(n∆) since ev-
ery sensor exchanges information with its neighbors
and the second pass takes O(w∆) where w is the num-
ber of white nodes left after the first pass and w ≤ n.
Lemma 1: The nodes colored Black at the end of
Phase 1 represent a Dominating Set for the graph G.
Proof: Assume that at the end of Phase 1, there
exists a node that is still colored white (i.e., it is not
adjacent to a black node or colored black itself). In the
second pass (that every white sensor goes through),
each sensor either adds either itself or a neighbor to
the dominating set. If a sensor is added to the dom-
inating set, all its white neighbors are colored grey.
Hence all white nodes must be either grey or black
when the second pass of Phase 1 concludes. There-
fore, such a node cannot exist and the set of black
nodes is dominating.

3.2 Phase 2: Connecting the
Dominating Set
In this subsection we will present our connection al-
gorithm. However, before we can do so, we need
to prove some properties of the dominating set con-
structed at the end of Phase 1 since we rely on
these properties to come up with the construction
that connects the disconnected dominating compo-
nents formed at the end of Phase 1.
Lemma 2: Any component of a dominating set is
separated by at most two vertices from another com-
ponent.
Proof: Assume there is a component separated
from all other components by at least three vertices
at the end of the algorithm. We can visualize this sce-
nario as COMP1 − a − b − c − COMP2 where a, b, c
are the three vertices separating COMP1 and COMP2.
Clearly the nodes a and c are dominated by the two
components. Also, by Lemma 1, b must be adjacent
to or in the dominating set. If b is dominated by a dif-
ferent component, this would create a path of length
two from both COMP1 and COMP2 to the component
dominating b, thereby leading to a contradiction.
Lemma 3: Connecting the dominating set created
by the greedy algorithm takes adding at most 2(n − 1)
vertices to the dominating set where n is the number
of components of the dominating set.
Proof: Base Case: Consider a dominating set of
two components. By Lemma 2 there are at most two
vertices need to connect this set. Thus the base case
holds: to connect a set of two components we need
at most 2 = 2(2 − 1) vertices. By the inductive hy-
pothesis a dominating set of n − 1 components can
be connected with 2((n −1) − 1) = 2(n −2) = 2n −4
components. By Lemma 2, another component is at
most 2 vertices away. Then the limit for n components
is 2n − 4 +2 = 2n − 2 = 2(n − 1) vertices.
Based on these two lemmas we now present the
connection phase of our algorithm. We make the as-
sumption that every sensor has a unique identifier as-
sociated with it. As can be seen from the algorithm
below, we initialize the component id of each grey
sensor to -1 and for every connected dominating com-
ponent, we initialize its component number to that of
the highest id sensor in that connected component.
This allows every component to have an associated
id - that of the highest id sensor in that component.
Now, if a grey is connected to two components with
different id’s, it colors itself black (in order to connect
these two components). It also updates its id to that
of the largest of these components. Since two compo-
nents can be at most two hops away (by Lemma 2), in
the next for loop, we check if any pair of sensors con-
nects two disconnected dominating components and
color this pair black.
Require: Recursively compute a component number
based on the id of the largest id sensor for that com-
ponent. Initialize all dominatees (grey) to an com-
ponent number of -1.
for all non-dominating (grey) nodes in V do
if v is connected to two dominating components
with different IDs then
v.COLOR ← BLACK
v.ID ← max component ID of the compo-
nents it connects
end if
end for
for every pair (u,v) of non-dominating connected
sensors do
highU ← max(N(u).ID)
highV ← max(N(v).ID)
if (highU 6= highV) then
u.COLOR ← BLACK
v.COLOR ← BLACK
change v.ID and u.ID to the component ID of
the component they joined
end if
end for
3.3 An example
We will now look at an example of both phases in
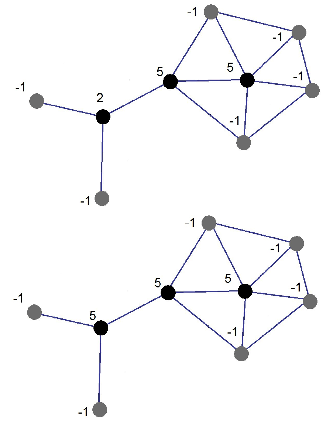
operation. We use the network shown in Figure 1 as
our exemplar. The figure shows the sensors and the
resulting graph representing the network. As men-
tioned in (Zhang and Hou, 2005), the transmission ra-
dius is double the sensing radius. At the start of the
algorithm all vertices are colored white (shown here
in yellow). The number next to each sensor indicates
its white neighbor count which at initialization is just
the degree of each node.
In the first round of Phase 1 each vertex checks if it
has the highest (or tied highest) white neighbor count
in its neighborhood. If so, it adds itself to the dom-
inating set (denoted in black) and tells all its neigh-
bors they have been dominated (denoted in gray). If
not, the vertex waits for round two. Since each ver-
tex is discovering its white neighbor count simultane-
ously, in this example only the vertex of white neigh-
bor count five will add itself. The vertex connected to
two leaves was not added since it had a neighbor with
a higher white count. In the second pass, each of the
white sensors checks which neighbor has the highest
count (including itself) and tells that neighbor to add
itself to the dominating set. The coloring at the end of
each pass of Phase 1 along with the component id’s of
the two black nodes is shown in Figure 2. Here we as-