VU Research Portal
A reciprocity inequality for Gaussian Schell-model beams and some of it
consequences
Friberg, A.T.; Visser, T.D.; Wolf, E.
published in
Optics Letters
2000
DOI (link to publisher)
10.1364/OL.25.000366
document version
Publisher's PDF, also known as Version of record
Link to publication in VU Research Portal
citation for published version (APA)
Friberg, A. T., Visser, T. D., & Wolf, E. (2000). A reciprocity inequality for Gaussian Schell-model beams and
some of it consequences. Optics Letters, 25(6), 366-368. https://doi.org/10.1364/OL.25.000366
General rights
Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners
and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights.
• Users may download and print one copy of any publication from the public portal for the purpose of private study or research.
• You may not further distribute the material or use it for any profit-making activity or commercial gain
• You may freely distribute the URL identifying the publication in the public portal ?
Take down policy
If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately
and investigate your claim.
E-mail address:
vuresearchportal.ub@vu.nl
Download date: 10. Aug. 2022

366 OPTICS LETTERS / Vol. 25, No. 6 / March 15, 2000
A reciprocity inequality for Gaussian Schell-model beams
and some of its consequences
Ari T. Friberg
Department of Physics—Optics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Taco D. Visser
Department of Physics and Astronomy, Free University, De Boelelaan, 1081 HV Amsterdam, The Netherlands
Emil Wolf
Department of Physics and Astronomy and Rochester Theory Center for Optical Science and Engineering,
University of Rochester, Rochester, New York 14627
Received November 12, 1999
A reciprocity inequality is derived, involving the effective size of a planar, secondary, Gaussian Schell-model
source and the effective angular spread of the beam that the source generates. The analysis is shown to imply
that a fully spatially coherent source of that class (which generates the lowest-order Hermite – Gaussian laser
mode) has certain minimal properties.
2000 Optical Society of America
OCIS code: 030.1640.
An important class of partially coherent beams are
the so-called Gaussian Schell-model beams (Ref. 1,
Sect. 5.6.4). They are generated by planar, secondary
sources whose intensity distribution I
共0兲
共r, n兲 at fre-
quency n and whose spectral degree of coherence
(Ref. 1, Sect. 4.3.2) m
共0兲
共r
1
, r
2
, n兲⬅g
共0兲
共r
2
2 r
1
, n兲
across the source plane z 苷 0 are both Gaussian; i.e.,
they have the form (see Fig. 1)
I
共0兲
共r, n兲 苷 A
2
共n兲exp关2r
2
兾2s
2
I
共n兲兴 , (1)
g
共0兲
共r
2
2 r
1
, n兲 苷 exp关2共r
2
2 r
1
兲
2
兾2s
2
g
共n兲兴 . (2)
In these formulas r, r
1
, and r
2
are position vectors
of points in the source plane and A共n兲, s
I
共n兲, and
s
g
共n兲 are positive constants. From now on we will not
display the dependence of the various parameters on n.
With a suitable choice of the parameters such a source
generates a beam. In the coherent limit 共s
g
! `兲 the
beam is just the lowest-order Hermite–Gaussian laser
mode.
Properties of beams of this kind have been exten-
sively studied in the literature. It has been predicted
theoretically (Ref. 2 or Ref. 1, Sect. 5.4.2) that a certain
trade-off is possible between the parameters s
I
and s
g
,
which characterize sources with different intensity dis-
tributions and different coherence properties, yet each
of these sources will generate the same far-zone inten-
sity distribution as a single-mode laser. This predic-
tion was confirmed experimentally soon afterward.
3,4
In this Letter we derive a simple reciprocity inequal-
ity that involves the angular spread of a Gaussian
Schell-model beam and the effective width of the inten-
sity profile of its source, and we derive some interesting
consequences from it.
We recall that the radiant intensity in the direction
specified by a unit vector s generated by a Gaussian
Schell-model source is given by the expression
J共s, n兲 苷 b
2
exp共2au
2
兾2兲 , (3)
where u is the angle that the vector s makes with the
normal to the source plane,
b 苷 共kAs
I
d兲 , a 苷 k
2
d
2
, (4)
with
1
d
2
苷
1
共2s
I
兲
2
1
1
s
2
g
,
(5)
k 苷 2pn兾c . (6)
Formula (3) follows at once from Eq. (5.4-16) of Ref. 1
in the paraxial approximation 共cos u 艐 1, sin u 艐 u兲
appropriate to a beam.
Fig. 1. Illustrating the notation.
0146-9592/00/060366-03$15.00/0 2000 Optical Society of America

March 15, 2000 / Vol. 25, No. 6 / OPTICS LETTERS 367
Let us now calculate the angular spread, Du say, of
the beam, defined by the formula
共Du兲
2
苷
R
p/2
0
u
2
关J共u兲兴
2
du
R
p/2
0
关J共u兲兴
2
du
.
(7)
Since J共u兲 is sharply peaked around the direction u 苷
0, we may extend the range of integration from 共0, p兾2兲
to 共0, `兲 in the integrals in Eq. (7), without introducing
an appreciable error. On substituting for J共u兲 from
the expression (3), one readily finds that
Du 苷
1
p
2
1
kd
.
(8)
The effective width Dr of the intensity profile of the
source, defined by the expression
共Dr兲
2
苷
R
r
2
关I
共0兲
共r兲兴
2
d
2
r
R
关I
共0兲
共r兲兴
2
d
2
r
,
(9)
with I
共0兲
共r兲 given by the formula (1) and with the
integration extending over the whole source plane z 苷
0, is readily found to have the value
Dr 苷 s
I
. (10)
It follows from Eqs. (8) and (10) that for all Gaussian
Schell-model beams
共Du兲共Dr兲 苷
s
I
kd
p
2
(11)
or, more explicitly, if we substitute for d from Eq. (5),
共Du兲共Dr兲 苷
1
k2
p
2
∑
1 1 4
µ
s
I
s
g
∂
2
∏
1/2
.
(12)
Several interesting consequences follow from for-
mula (12). First, we note that if the source is com-
pletely spatially coherent, i.e., when s
g
! `, Eq. (12)
gives
共Du兲
coh
共Dr兲 苷
1
k2
p
2
,
(13)
where 共Du兲
coh
denotes the angular spread of the
coherent Gaussian Schell-model beam. On dividing
Eq. (12) by Eq. (13), we obtain the result that
共Du兲 苷 共Du兲
coh
∑
1 1 4
µ
s
I
s
g
∂
2
∏
1/2
.
(14)
Since the factor multiplying 共Du兲
coh
on the right neces-
sarily exceeds unity, it follows that
Du . 共Du兲
coh
(15)
for all partially coherent Gaussian Schell-model beams.
Stated in words, the inequality (15) asserts that among
all planar, secondary Gaussian Schell-model sources
of the same effective width Dr ⬅ s
I
of the intensity
profile, the completely coherent one will generate the
most directional beam. As we already noted, the
limiting, fully coherent case represents the lowest-
order Hermite–Gaussian beam.
Next let us consider Gaussian Schell-model beams
that have the same effective angular spread Du but are
generated by sources with different effective widths Dr
of their intensity profiles. For the fully coherent case
we have from Eq. (12), on taking the limit s
g
! ` while
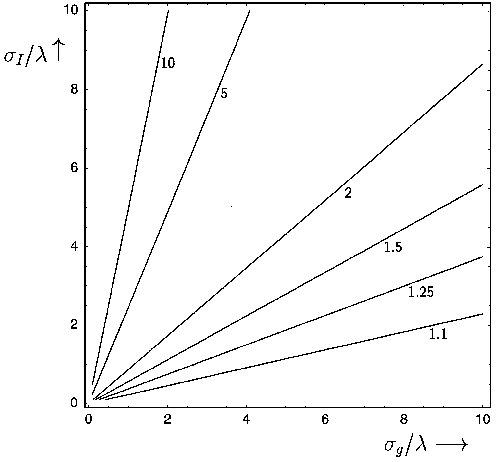
Fig. 2. Contours of the factor
∑
1 1 4
µ
s
I
s
g
∂
2
∏
1/2
,
which represents the ratios Du兾共Du兲
coh
and Dr兾共Dr兲
coh
.
[Eqs. (14) and (17)].
Fig. 3. The factor
∑
1 1 4
µ
s
I
s
g
∂
2
∏
1/2
plotted as a function of the parameter s
I
兾s
g
.

368 OPTICS LETTERS / Vol. 25, No. 6 / March 15, 2000
keeping Du fixed,
共Du兲共Dr兲
coh
⬅
1
k2
p
2
.
(16)
On dividing Eq. (12) by Eq. (16) we find that
共Dr兲 苷 共Dr兲
coh
∑
1 1 4
µ
s
I
s
g
∂
2
∏
1/2
(17)
for all Gaussian Schell-model beams. This formula
implies that among all planar, secondary, Gaussian
Schell–model sources which generate beams of the
same angular spread Du, the fully coherent one has
the smallest effective size. These results are in agree-
ment with some computations presented in Refs. 2 and
5. Figures 2 and 3 show the behavior of the impor-
tant factor 关1 1 4共s
I
兾s
g
兲
2
兴
1/2
as function of s
I
, s
g
,
and s
I
兾s
g
.
This research was supported by the U.S. Air Force
Office of Scientif ic Research under grant F 49620-96-
1-0400 and by the Engineering Research Program of
the Office of Basic Engineering Sciences of the U.S.
Department of Energy, under grant DE-FG02-90 ER
14119.
This investigation was carried out in response to an
interesting question posed by Richard Albanese.
References
1. L. Mandel and E. Wolf, Optical Coherence and Quantum
Optics (Cambridge University Press, Cambridge, 1995).
2. E. Wolf and E. Collett, Opt. Commun. 25, 293 (1978).
3. P. De Santis, F. Gori, G. Guattari, and C. Palma, Opt.
Commun. 29, 256 (1979).
4. J. D. Farina, L. M. Narducci, and E. Collett, Opt.
Commun. 32, 203 (1980).
5. J. T. Foley and M. S. Zubairy, Opt. Commun. 26, 297
(1978).