Particle Swarm Optimization in Dynamic
Environments
Tim Blackwell
Department of Computing, Goldsmiths College London SE14 6NW, UK
t.blackwell@gold.ac.uk
1 Introduction
Particle Swarm Optimization (PSO) is a versatile population-based o ptimiza-
tion technique, in many respects simila r to evolutionary algorithms (EAs).
PSO has been shown to perform well fo r ma ny static problems [30]. However,
many real-world problems are dynamic in the s ense that the global optimum
location and value may change with time. The task for the optimization al-
gorithm is to track this shifting optimum. It has been argued [14] that EAs
are potentially well-suited to such tasks, and a re view of EA variants tested
in the dy namic problem is given in [13, 15]. It might be wondered, therefore,
what promise P SO holds for dynamic problems.
Optimization w ith particle swarms has two major ingredients, the particle
dynamics and the particle information network. The particle dynamics are de-
rived from swarm simulations in computer graphics [21], and the information
sharing component is inspired by social networks [32, 25]. These ingredients
combine to make PSO a robust and efficient optimizer of real-valued objective
functions (although PSO has also been successfully applied to combinatorial
and discrete problems too). PSO is an accepted computational intelligence
technique, sharing some qualities with Evolutionary Computation [1].
The application of PSO to dynamic problems has been explored by various
authors [30, 23, 17, 9, 6, 24]. The overa ll consequence of this work is that PSO,
just like EAs, must be modified for optimal results on dyna mic environments
typified by the moving peaks benchmark (MPB). (Moving peaks, arguably
representative of real world problems, consist of a number of peaks of changing
with and height and in lateral motion [12, 7 ].) The or igin of the difficulty lies
in the dual problems of outdated memory due to environment dynamism, and
diversity loss, due to convergence.
Of these two problems, diversity loss is by far the more serious; it has
been demonstrated that the time taken for a partia lly converged swarm to
re-diversify, find the shifted peak, and then re-converge is quite deleterious
to performance [3]. Clearly, either a re-diversification mechanism must be

2 Tim Blackwell
employed at (or before) function change, and/or a measur e of diversity can be
maintained throughout the run. There are four principle mechanisms for either
re-diversification or diversity maintenance: randomization [23], repulsion [5],
dynamic networks [24, 36] and multi-populations [29, 6].
Multi-swarms combine repulsion with multi-populations [6, 7]. Interest-
ingly, the repulsion occurs between particles, and between swarms. The multi-
population in this case is an interacting super-swarm of charged swarms . A
charged swarm is inspired by mo dels of the atom: a conventional PSO nu-
cleus is surrounded by a cloud of ‘charged’ particles. The charged particles
are responsible for maintaining the diversity of the swarm. Furthermore, and
in ana logy to the exclusion pr inciple in atomic physics, each swarm is subject
to an ex c lus ion pr e ssure that operates when the swarms collide. This prohibits
two or more swarms from sur rounding a single peak, thereby enabling swarms
to watch s e c ondary peaks in the eventuality that these peaks might become
optimal. This strategy has proven to be very effective for MPB environments.
This chapter starts with a description of the canonical PSO algo rithm
and then, in Section 3, explains why dyna mic environments pose par ticula r
problems for unmodified PSO. The MPB framework is also introduced in
this se c tion. The following section describes some PSO variants that have
been proposed to dea l with diversity loss. Section 5 outlines the multi-swarm
approach and the subsequent section pres e nts new results for a self-adapting
multi-swarm, a multi-population with swarm birth and death.
2 Canonical PSO
In PSO, population members (particles) possess a memory of the best (with
respect to an objective function) loc ation that they have visited in the past,
pbest, and of its fitness. In addition, particles have access to the best location
of any other particle in their own network. These two locations (which will
coincide for the best pa rticle in any networ k) become attractors in the search
space of the swarm. Each par ticle will b e repeatedly drawn back to spatial
neighborhoods close to these two attractors, which themselves will be updated
if the glo bal best and/or particle best is be ttere d at each particle update.
Several network topologies have been tr ied, with the star or fully connected
network remaining a popular choice for unimodal functions. In this network,
every particle will share information with every other particle in the swarm so
that there is a sing le gbest g lobal best attrac tor representing the best location
found by the entire swarm.
Particles p ossess a velocity which influences position updates according to
a simple disc retization of particle motion
v(t + 1) = v(t) + a(t + 1) (1)
x(t + 1) = x(t) + v(t + 1) (2)

Particle Swarm Optimization in Dy namic Environments 3
where a, v, x and t are acceleration, velocity, p osition and time (iteration
counter) respectively. Eqs. 1, 2 are similar to particle dynamics in swarm sim-
ulations, but PSO particles do not follow a smooth trajectory, instead moving
in jumps, in a motion known as a flight [28] (notice that the time increment
dt is missing from these rules). The particles experience a linear or spring-
like a ttraction, weighted by a random number, (particle mass is set to unity)
towards each attra c tor. Convergence towards a good solution will not fo llow
from these dynamics alone; the particle flight must progressively contract.
This contraction is implemented by Clerc and Kennedy with a constriction
factor χ, χ < 1 , [20]. For our purposes here, the Cle rc-Kennedy PSO will be
taken as the canonical swarm; χ replace s other energy draining factors extant
in the liter ature such as a decreasing ‘iner tial weight’ and velocity cla mping.
Moreover the constricted swarm is replete with a convergence proof, albeit
about a static attractor (although there is some experimental and theoretical
support for c onvergence in the fully interacting swarm where particles can
move attractors [10]).
Explicitly, the acceleration of particle i in Eq.1 is given by
a
i
= χ[cǫ · (p
g
− x
i
) + cǫ · (p
i
− x
i
)] − (1 − χ)v
i
(3)
where ǫ are vectors of random numbers drawn fro m the uniform distribution
U[0, 1], c > 2 is the spr ing constant and p
i
, p
g
are particle and global attra c -
tors. This formulation o f the particle dynamics has been chosen to demon-
strate explicitly constriction as a frictional fo rce, opposite in direction, and
proportional to, veloc ity. Clerc and Kennedy derive a relation for χ(c): stan-
dard values are c = 2.05 and χ = 0.729843788. T he complete PSO algorithm
for maximizing an objective function f is summarized as Algorithm 1.
3 PSO problems with moving peaks
As has be en mentioned in Sect 1, PSO must be modified fo r optimal results
on dynamic environments typified by the moving pea ks benchmark (MPB).
These modifications must solve the pr oblems of outdated memory, and of lost
diversity. This explains the origins of these problems in the context of MPB,
and shows how memory loss is easily addressed. The following section then
considers the second, more severe, problem.
3.1 Moving Peaks
The dynamic objective function of MPB, f(x, t), is optimized at ‘peak’ lo-
cations x
∗
and has a global optimum at x
∗∗
= arg max{f(x
∗
)} (once more,
assuming optimization means ma ximizing). Dynamism entails a small move-
ment of magnitude s, and in a random direction, of each x
∗
. This happens

4 Tim Blackwell
Algorithm 1 Canonical PSO
FOR EACH particle i
Randomly initialize v
i
, x
i
= p
i
Evaluate f (p
i
)
g = arg max f(p
i
)
REPEAT
FOR EACH particle i
Update particle position x
i
according to eqs.. 1, 2 and 3
Evaluate f (x
i
)
//Update personal best
IF f (x
i
) > f(p
i
) THEN
p
i
= x
i
//Update global best
IF f (x
i
) > f(p
g
) THEN
p
g
= arg max f(p
i
)
UNTIL termination criterion reached
every K evaluations and is accompanied by small changes o f pea k height and
width. There are p peak s in total, although some peaks may bec ome obscured.
The peaks are constrained to move in a search space of extent X in each of
the d dimensions, [0, X]
d
.
This scenario, which is no t the most ge neral, nevertheless has been put
forward as representative of real world dynamic problems [12] and a bench-
mark function is publicly available for download from [11]. Note that small
changes in f(x
∗
) can still invoke large changes in x
∗∗
due to peak promotion,
so the many peaks model is far from trivial.
3.2 The problem of outdated memory
Outdated memo ry happ ens at environment change when the optima may shift
in location and/or value. Particle memory (namely the best location visited
in the past, and its co rresponding fitnes s) may no longer be true at change,
with potentially disastrous effects on the search.
The problem of outdated memory is typically solved by either assuming
that the algorithm knows just when the environment change occurs, or that
it can detect change. In either case, the algor ithm must invoke a n appr opriate
response. One method of detecting change is a re-evaluation of f at one or
more of the personal b e sts p
i
[17, 23]. A simple and effective response is to
re-set all particle memories to the current particle position and f value at this
position, and e ns uring that p
g
= arg max f(p
i
). One possible dr awback is that
the function has not changed at the chosen p
i
, but has changed els e w here.
This can be remedied by re- e valuating f at all personal bests, at the expense
of doubling the to tal number of function e valuations per iteration.

Particle Swarm Optimization in Dy namic Environments 5
3.3 The problem of lost diversity
Equally troubling as outdated memory is insufficient diversity at change. The
population takes time to re-diversify and re-converge, effectively unable to
track a moving optimum.
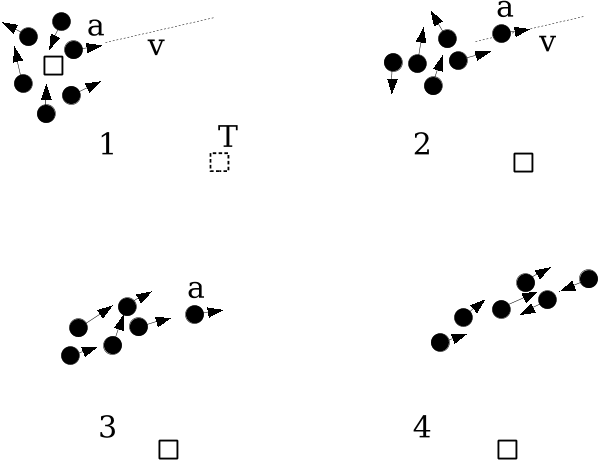
It is helpful at this stage to introduce the swarm diameter |S|, defined
as the larg e st distance, along any axis, between any two particles [2], as a
measure of swarm diversity (Fig. 1). Loss of diversity arises when a swarm
is co nverging on a peak. There are two possibilities: when change occurs, the
new optimum location may either be within or outside the collapsing swarm.
In the former case, there is a good chance that a particle will find itself close to
the new optimum within a few iterations and the swarm will successfully track
the moving target. The swarm as a whole ha s sufficient diversity. However,
if the optimum shift is significantly far from the swarm, the low velocities
of the particles (which are of order |S|) will inhibit re-diversification and
tracking, and the swarm can even o scillate about a false attractor and along
a line perpendicular to the true optimum, in a phenomenon known as linear
collapse [5]. This effect is illustr ated in Fig. 2.
Fig. 1. The swarm diameter
These considerations can be quantified with the help of a prediction for
the rate of diversity loss [2, 3, 10]. In general, the swa rm shrinks at a rate
determined by the constriction facto r and by the local environment at the
optimum. For static functions with spherical symmetric basins of attraction,
the theoretical and empirical analysis of the above references suggest that the
rate of shrinkage (and hence diversity loss) is scale invariant and is given by
a scaling law
|S(t)| = Cα
t
(4)
for constants C a nd α < 1, where α ≈ 0.92 and C is the swarm diameter
at iteration t = 0. T he number of function evaluations between change, K,
can be converted into a period measured in iterations, L by considering the