UC Berkeley
Coleman Fung Risk Management Research Center Working
Papers 2006-2013
Title
A Class of Singular Control Problems and the Smooth Fit Principle
Permalink
https://escholarship.org/uc/item/8w46j0td
Authors
Guo, Xin
Tomecek, Pascal
Publication Date
2007-10-07
eScholarship.org Powered by the California Digital Library
University of California

University of California
Berkeley
Working Paper # 2007 -05
A Class of Singular Control Problems
and the Smooth Fit Principle
Xin Guo, UC Berkeley and Cornell University
Pascal Tomecek, Cornell University
October 7,2007

A Class of Singular Control Problems and the Smo oth Fit
Principle
∗
Xin Guo
†
UC Berkeley and Cornell
Pascal Tomecek
‡
Cornell University
October 7, 2007
Abstract
This paper analyzes a class of singular control problems for which value functions
are not necessarily smooth. Necessary and sufficient conditions for the well-known
smooth fit principle, along with the regularity of the value functions, are given. Explicit
solutions for the optimal policy and for the value functions are provided. In particular,
when payoff functions satisfy the usual Inada conditions, the boundaries between action
and no-action regions are smooth and strictly monotonic as postulated and exploited in
the existing literature (Dixit and Pindyck (1994); Davis, Dempster, Sethi, and Vermes
(1987); Kobila (1993); Abel and Eberly (1997); Øksendal (2000); Scheinkman and
Zariphopoulou (2001); Merhi and Zervos (2007); Alvarez (2006)). Illustrative examples
for both smooth and non-smooth cases are discussed, to highlight the pitfall of solving
singular control problems with a priori smoothness assumptions.
∗
This research is generously supported by grants from OpenLink Fund at the Coleman Fung Risk Man-
agement Research Center at UC Berkeley
†
Department of Industrial Engineering and Operations Research, UC Berkeley, CA 94720-1777, USA,
Phone (510) 642 3615, email: xinguo@ieor.berkeley.edu.
‡
Scho ol of Operations Research and Industrial Engineering, Cornell University, Ithaca, NY 14853-3801,
USA, Phone (607) 255 1270, Fax (607) 255 9129, email: pascal@orie.cornell.edu.
1

1 Introduction
Consider the following problem in reversible investment/capacity planning that arises nat-
urally in resource extraction and power generation. Facing the risk of market uncertainty,
companies extract resources (such as oil or gas) and choose the capacity level in response
to the random fluctuation of market price for the resources, subject to some capacity con-
straints, as well as the associated costs for capacity expansion and contraction. The goal of
the company is to maximize its long-term profit, subject to these constraints and the rate
of resource extraction.
This kind of capacity planning with price uncertainty and partial (or no) reversibility
originated from the economics literature and has since attracted the interest of the ap-
plied mathematics community. (See Dixit and Pindyck (1994); Brekke and Øksendal (1994);
Davis, Dempster, Sethi, and Vermes (1987); Kobila (1993); Abel and Eberly (1997); Baldurs-
son and Karatzas (1997); Øksendal (2000); Scheinkman and Zariphopoulou (2001); Wang
(2003); Chiarolla and Haussmann (2005); Guo and Pham (2005) and the references therein.)
Mathematical analysis of such control problems has evolved considerably from the initial
heuristics to the more sophisticated and standard stochastic control approach, and from
the very special case study to general payoff functions. (See Harrison and Taksar (1983);
Karatzas (1985); Karatzas and Shreve (1985); El Karoui and Karatzas (1988, 1989); Ma
(1992); Davis and Zervos (1994, 1998); Boetius and Kohlmann (1998); Alvarez (2000, 2001 );
Bank (2005); Boetius (2005)). Most recently, Merhi and Zervos (2007) analyzed this problem
in great generality and provided explicit solutions for the special case where the payoff is of
Cobb-Douglas type. Their method is to directly solve the HJB equations, assuming certain
regularity conditions for both the value function and the boundaries between the action and
no-action regions. Guo and Tomecek (2007) later established sufficient conditions for the
smoothness of the value function by connecting the singular control problem with a collection
of optimal switching problems.
However, for many singular control problems in reversible investment and in areas such
as queuing and wireless communications (Martins, Shreve, and Soner (1996); Assaf (1997);
Harrison and Van Mieghem (1997); Ata, Harrison, and Shepp (2005)), there is no regularity
for either the value function or the boundaries. Therefore, two important mathematical issues
remain: 1) necessary conditions for regularity properties; and 2) characterization for the
value function and for the action and no-action regions when these regularity conditions fail.
Understanding these issues is especially important in cases where only numerical solutions
are available, and for which the assumption on the degree of the smoothness is wrong (see
also discussions in Section 5.2).
This paper addresses these two issues via the study of a class of singular control problems.
Both necessary and sufficient conditions on the differentiability of the value function and on
the smooth fit principle are established. Moreover, these conditions lead to a derivative-
based characterization of the investment, disinvestment and continuation regions even for
non-smooth value functions. In fact, when the payoff function is not smooth, this paper is the
2

first to rigorously characterize the action and no-action regions, and to explicitly construct
both the optimal policy and the value function. To be consistent with the literature in
(ir)reversible investment, the running payoff function in this paper depends on the resource
extraction rate and the market price in the form of H(Y )X
λ
. It is worth noting that H(·)
is any concave function of the capacity, and may be neither monotonic nor differentiable.
This includes the special cases investigated by Guo and Pham (2005); Merhi and Zervos
(2007); Guo and Tomecek (2007). In particular, when H satisifies the well-known Inada
conditions (i.e., continuously differentiable, strictly increasing, strictly concave, with H(0) =
0, H
0
(0
+
) = ∞, H
0
(∞) = 0), our results show that the boundaries between regions are
indeed continuous and strictly increasing as postulated and exploited in previous works:
Dixit and Pindyck (1994); Davis, Dempster, Sethi, and Vermes (1987); Kobila (1993); Abel
and Eberly (1997); Øksendal (2000); Scheinkman and Zariphopoulou (2001); Merhi and
Zervos (2007); Alvarez (2006). Also note that our method can be applied to more general
(diffusion) processes for the price dynamics, other than the geometric Brownian motion
assumed for explicitness in this paper. Finally, the construction between the functional form
of the boundaries and the payoff function itself is also novel, as the value function and the
boundaries may be neither smooth nor strictly monotonic as in the existing literature.
The most relevant and recent work to this paper is Alvarez (2006), which provides a
great deal of economic insight into the problem. However, Alvarez (2006) only handles
payoff functions satisfying the Inada conditions. In contrast, our solution is independent of
the regularity of the payoff and value functions.
Outline. The control problem is formally stated, with its value function and optimal p olicy
described in Section 2; details of the derivation are in Section 3. The main result of this
paper regarding the regularity of the value function is in Section 4. Examples are provided
in Section 5, including cases for which the value function is not differentiable, the optimal
controlled process not continuous, the boundaries of the action regions not smooth, and the
interior of the continuation region not simply connected.
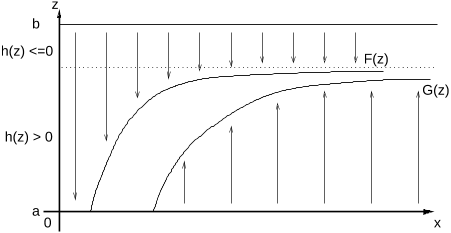
2 Mathematical Problem and Solution
2.1 Problem
Let (Ω, F, F, P) be a filtered probability space and assume a given bounded interval [a, b] ⊂
(−∞, ∞). Consider the following problem:
Problem A.
V
H
(x, y) := sup
(ξ
+
,ξ
−
)∈A
00
y
J
H
(x, y; ξ
+
, ξ
−
),
3