A FUZZY ACOUSTIC-PHONETIC DECODER
FOR SPEECH RECOGNITION
Olivier OPPIZZI, David FOURNIER, Philippe GILLES, Henri MELONI
CERI - Laboratoire d'informatique, AVIGNON, FRANCE
ABSTRACT
In this paper, a general framework of acoustic-phonetic
modelling is developed. Context sensitive rules are
incorporated into a knowledge-based automatic speech
recognition (ASR) system and are assessed with control based
on fuzzy decision making. The reliability measure is outlined: a
tests collection is run and a confusion matrix is built for each
rule. During the recognition procedure the fuzzy set of trained
values related to the phonetic unit to be recognized is
computed, and its membership function is automatically drawn.
Tests were done on an isolated-word speech database of French
with 1000 utterances and with 33 rules. The results with a one-
speaker low training rate are established via a two-step
procedure: a word recognition and a word rejection test bed with
five speakers who were never involved during the training.
1. INTRODUCTION
Speech Understanding is considered as a dynamic process
through linguistic levels with a high combinatory complexity.
By essence, work in the field of speech recognition tends to
prune research spaces so as to reduce lexical hypothesis to be
further computed by a semantic level. The goal of the described
work is the development of a rule-based isolated-word ASR
system which will give the user a means to incorporate, assess
and apply into a fuzzy framework new rules to be involved in
reducing a lexical cohort.
2. RECOGNITION RULES
2.1 Multi-Stage Decoding
A bottom-up, rule-based, acoustic-phonetic decoder retrieves
the segments and context-free features from isolated words [4].
Then, a word recognizer [1] provides a set of concurrent lexical
hypotheses from the previous phonetic lattice (Figure 1).
Signal (word "peek")
bottom-up APD
+ lexical access
top-down APD
word 1: a
parameters
word 2:
t
ik
p
LATTICE
Figure 1: Principles of a multi-stage decoder.
To improve the recognition rate, a top-down decoder is now
able to focus on phonetic transitions and to verify co-
articulation cues. This environment allows the user to program
context sensitive rules since all phonetic hypothesis are
available during the top-down stage.
2.2 Contextual Rules
The system combines three sets of recognition rules which
analyse the spectral characteristics of the vocal tract to
compute co-articulation features for French. The speaker
references are obtained with a low training procedure
(30 spoken words). The decoder samples input speech at
12800 Hz and divides it into frames every 10ms. A set of 24
mel-scaled LPC based cepstrum, energy, zero-crossing and delta
zero-crossing rates are computed for each frame.
F1 increases if /k,g,r/ appears in context. Let V be
the current spoken vowel hypothesis, L be the frequency band
of F1 references whatever the vowel and S the frequency band
of V-like vowel references (figure 2). S is shifted in a /k/ or /g/
or /r/ context hypothesis so as to open the formant location.
The rule returns (M
S
-M
L
) where M
S
is the spectral maximum of
band S and M
L
the maximum of band L. The returned value is
expected to be positive if V is a vowel in such an opening
context.
i
r (hypothesis)
frame close to /i/ reference frame
min(F1 of /i,y,u/ references)
max(F1 of /i,y,u/ references)
SL
min(F1 of all vowels)
max(F1 of all vowels)
Figure 2: F1 increasing in /k,g,r/ context.
Stop-consonants' burst. The frequency band where burst
occurs depends on the right context. Let V be the stop-
consonant to be analysed and L be the frequency band where
the burst is expected to be found. For instance, if the following
phoneme is /i/, L starts from the first channel to channel
(F2+1) where F2 is extracted from the V-spectral reference. The
rule returns the peak value in L.
High frequency slice of /s,∫/ spectrum. The highest
delta high frequency C is extracted from the fricative reference.
C becomes a band L depending on the right phoneme. For
example, if the right context is /i,e,t,d/, L is [C-1,24]. The
rule returns the higher slice in L.

3. FUZZY DECISION MAKING
3.1 Fuzzy Versus Classical Control.
A classical processing of acoustic-phonetic rules includes
thresholdings anf hierarchical control, as illustrated in
figure 3, to recognize voiceless fricatives.
rule_FF(unit)
f = frame such that (f-1) and (f+1) spectra are the closest
S = spectrum of f
Max = higher value of S in high frequencies
Min = lower value of S in low frequencies
if( |Max-Min| < Threshold1 ) then return /f/ else return ?
rule_SSCH(unit)
S = spectrum of frame f such that (f-1) and (f+1) spectra
are the most distant
F = frequency of S where delta is the highest
if( F < Threshold2 ) then return /∫/ else return /s/
CONTROL: rule_FFSSCH(u)
if( rule_FF(u) ≠ ? ) then return /f/ else return rule_SSCH(u)
Figure 3: Hierarchical decision in a speech recognizer.
A distinctive feature of our system is that the control runs under
a fuzzy model combined to a least-commitment decision
approach. Thus, particular attention has been devoted to the
decision module so that thresholds and hierarchic description of
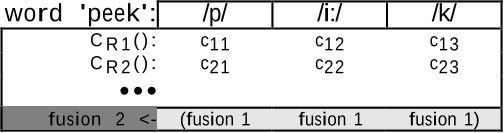
knowledge are avoided. In table 1, C
Ri
() is a reliability measure
applied to rule R
i
. and c
ij
corresponds to the degree of
certainty to detect phoneme j knowing the result of rule R
i
.
word 'peek': /p/ /i:/ /k/
C
R1
(): c
11
c
12
c
13
C
R2
(): c
21
c
22
c
23
•••
fusion 2 <- (fusion 1 fusion 1 fusion 1)
Table 1: Fuzzy decision in a speech recognizer.
fusion1 and fusion2 are aggregation operators. fusion1
gives a degree of certainty to every phonetic unit of the lattice,
fusion2 computes a lexical score.
To obtain a well-defined decision model, particular attention
has been paid to rules integration: although values returned by
rules can be either of numerical or of symbolic nature (the
reliability measure translates multi-domain values
onto [0,1]), rules have been adjusted to fit the dynamic
ranges of the acoustic cues, whatever the phonetic units to be
decoded. Indeed, no more hierarchical structure can prevent a
rule from analysing of sound with or without such or such a
property, as rule_ffssch() in figure which assumes
rule_ssch() to analyse a non-/f/ phoneme. Hence,
robustness has become a major issue.
3.2 A Reliability Measure.
Using fuzzy sets initiated by [5], the platform provides a
reliability measure in order to gain knowledge about the ability
of each rule and to perform rational fusion operators on such
degrees of uncertainty. This contribution is motivated by
automatic computations of acoustic cue fuzzy descriptions as
stated in [2].
Hence, the reliability measure is trained on an isolated-word
speech database. For every rule and phoneme, a histogram is
established from a confusion matrix. In figure 4, P1 is /i/, P2
is /y/, and R returns the F2-F4 slice. This parameter is expected
to be positive for /i/ and to be negative for /y/.
RULE R
phoneme
P1
occurrences
parameters
(values of R)
v
occurrences
parameters
(values of R)
value v appears n times
in P1 analysis
phoneme
Pn
n
•••
.....
Figure 4: Histograms of rule ability to recognize phonemes.
If R produced negative parameters in the P1 analysis, either
the phoneme shows a bad acoustic quality, or the rule is not
able to analyse correctly the variability of such a sound. Since
the relevance of a rule is related to these two factors, our
reliability measure corresponds to a relevance function.
During the recognition procedure, rule relevance may be
computed from such a set of histograms. Let H
R,Pi
() be the
histogram of rule R for the phonetic hypothesis P
i
to be
analysed. A fuzzy set is represented as a set of parameters (x-
axis in figure ). A fuzzy set and its membership function (the
relevance function) are built using H=H
R,Pi
() as the correct
recognition histogram and H'=H'
R,Pi
() as the wrong
recognition histogram such that:
H
R,P
i
'
: v→ H
R,P
i
'
v
()
= H
R,P
i
v
()
j≠i
∑
The j indices refer to phonemes P
j
which have been detected
into a P
i
equivalent signal portion within the lattice. Actually,
H'
R,Pi
() corresponds to the erroneous recognition histogram
of rule R for phonetic hypothesis P
i
against a set of candidate
phonemes. The way to elaborate the relevance function is
shown in figure 5 (parameters are along the x-axis).

word 1:
f
li
C (/i/)
p
p=R( /i/ )
H histogram of R for /i/
H' histogram of R for /i/
(against a set of
candidate phonemes)
peak detection
+ aggregation
R
Z' peak
Z peak
Z' block Z block
fuzzyfication
in [0,1]
.
.
Z' level
Z level
word 2:
f
a:
(candidate phoneme)
Figure 5: A relevance function as a membership function
built during the recognition procedure.
After peak detection over histograms, the procedure shows
reactive zones where correct and/or erroneous recognition
results have been trained. Levels of the reliability measure are
computed by a sophisticated function L() including
possibilist calculus and training rates. For a given rule:
Let N (resp. N' ) be the cardinality of histogram H (resp. H' )
Let Z be a block (interval of parameters) of H and Z' of H'
LZ
()
=
lZ/H
()
−lZ/H'
()
+1
2
lZ/H
()
=
∆Z
()
sup
z of H
∆ z
()
()
⋅
log
2
N
()
log
2
N
()
+4
⋅
log N
()
log max(N, N')
()
l(Z/H) comes out as the relevance of block Z knowing
histogram H. The first factor expresses the possibility [3] of a
Z block among blocks of H, with ∆(Z] the density of
block Z. The second and third factors decrease the result
respectively if H corresponds to an absolute low trainig rate
and if H corresponds to a low training rate relative to H'.
No training results over a given block Z is called ignorance
(that is, l(Z/H)=l(Z/H')=0). L() assures a normalization
constraint which causes ignorance to get a high uncertainty.
Once levels are computed, they are joined by lines. Thus, rule
domains have to be linear. Linear interpolation seems to be
relevant in fuzzy applications [3] as far as fuzzy
representations tend to capture unprecise data.
In this way, it is not necessary to engage a high training rate
procedure to have a fuzzy description of the reliability measure,
as it is by HMM decoding. Moreover, the reliability measure is
not a global measure. For a given rule, it varies according to the
parameter returned by a given rule and according to any pre-
decoding: in our ASR system, histograms are determined from
the bottom-up decoder ability to discriminate between sounds.
3.3 Aggregation
To compute a phonetic score knowing the reliability scores c
ij
(see fusion1 in table 1), the semantic interpretation of c
ij
is
used. As an average reliability score means either ignorance or
high uncertainty, the fusion1 operator solely trusts the lowest
and the highest score. If the N values of c
ij
are ordered for a
given phoneme j (c
1j
is the lowest and c
Nj
the highest
reliability score), fusion1 can be seen as an OWA
operator [7] with a null weight vector [w
i
]
1≤i≤N
but first and
last weight, expressing that c
1j
and c
Nj
scores are more
weighted as they go far from 0.5.
w
1
= c
1j
− 0.5
w
N
= c
Nj
− 0.5
∀i = 2,...,N −1
(
)
,w
i
= 0
and fusion1 =
w
i
⋅ c
ij
()
i=1
N
∑
w
i
()
i=1
N
∑
To compute fusion2 (Table 1), it is considered that a low
phonetic score coming from fusion1 implies a low lexical
score, that is, a word may be rejected if it is sure that one of its
phonetic hypotheses is not available in the speech signal. A
context independent variable behaviour operator [6] is used as
illustrated in figure 6. Let S
j
(i=1,...,P) be the P phonetic
scores to combine. The experimental weight function w()
tends to aggregate with the min() function if one of the S
j
corresponds to a low degree of certainty, otherwise tends to
aggregate with the arithmetical mean function.
fusion2 = wS
j
()
⋅min S
j
()
[]
+1−wS
j
⋅
S
j
j=1
P
∑
P
w()
min(Sj)
0
0.5
1
1
Figure 6: experimental weight function for aggregation.

4. PERFORMANCE
The evaluation speech data were selected from the BDLEX
database. The reliability measure was poorly trained using a
partial database collected from one male speaker. The isolated-
word recognition corpus consisted of 1000 words pre-
processed with a 20,000 word dictionary at bottom-up
decoding: a group of five speakers (four males, one female),
who were never involved during the learning stage, was
presented with 200 words each. Thus, the results show the
speaker-independent ability of the system. For every word to be
recognized, a 50 candidate word cohort was available. 33 rules
were applied during the top-down phase.
The experiment consisted of testing the recognition and the
rejection ability of the top-down decoder. Figure 7 shows the
correct recognition results in cumulated percentages and
table 2 the rejection rates among 49000 erroneous words and
1000 correct words.
0
20
40
60
80
100
1
7
13
19
25
31
37
43
49
Figure 7: correct recognition results.
threshold
on lexical score
erroneous words
rejection rate
correct words
rejection rate
10 2.31% 0.08%
16 11.3% 3.4%
20 40.6% 29.15%
Table 2: rejection rate according to a relevance threshold.
The top-down decoder fails to significantly improve the
performance of the bottom-up session. Firstly, only
ten phoneme-context dependent rules were tested. We hope the
system can perform better with the addition of such rules.
Secondly, examination of the fuzzy decision model shows that
reliability scores often correspond to a high degree of
uncertainty. Therefore, the decision itself becomes uncertain.
The system was observed to provide interesting but insufficient
rejection rates if the lexical score is below 16. The
aggregation model produces safe decisions as long as most of
the phonemes of a given word were not acoustically depreciated
(34 words are rejected at threshold=16 since two phonetic
scores at least per word were low due to two rules at least).
These results stress the importance of considering acoustic-
phonetic knowledge to reject erroneous lexical hypotheses
rather than obtaining a high recognition rate.
5. CONCLUSIONS
To summarize, we can say that fuzzy decision making has a
number of advantages compared with hierarchical control when
it comes to reject lexical hypotheses:
• Thresholds are delayed in the decision procedure;
• It is not necessary to extract a rule control procedure
from meta-knowledge;
• The multi-domain parameters produced by rules can be
compared and rationally aggregated after the
computation of the reliability measure.
The system presented above can be improved on in a number of
ways. One is the optimization of aggregation operators. On the
other hand, the relevance measure has a potential use in other
word rejection areas: speech recognition with HMM may
improve by evaluating a probability model from reliability
vectors, which is currently being investigated in a speaker
independent vocal dictation system.
6. ACKNOWLEDGMENTS
The authors would like to thank Renato De Mori for helpful
discussions.
7. REFERENCES
1. Béchet, F., Système de traitement de connaissances
phonétiques et lexicales: application à la
reconnaissance de mots isolés sur de grands
vocabulaires et à la recherche de mots cibles dans un
discours continu, PhD Thesis of the University of
Avignon, France, 1994.
2. De Mori, R., Computer Models of Speech using Fuzzy
Algorithms, Plenum Press, New York, 1983.
3. Dubois, D., Modèles mathématiques de l'imprécis et de
l'incertain en vue d'applications aux techniques d'aide à
la décision, PhD Thesis of the Institut National
Polytechnique de Grenoble, France, 1983.
4. Gilles, P, Décodage phonétique de la parole et
adaptation au locuteur, PhD Thesis of the University of
Avignon, France, 1993.
5. Zadeh, L.A., "Fuzzy Sets", Information Control: 338-
353, Vol. 8, 1965.
6. Bloch, I., Information Combination Operators for Data
Fusion: A Comparative Review with Classification,
Technical report n° 94 D 013, Ecole Nationale
Supérieure des Télécommunications, France, 1994
7. Yager, R.R., "On Ordered Weighted Averaging
Aggregation Operators in Multicriteria Decision-
Making", Readings in Fuzzy Sets for Intelligent
Systems: 80-87, 1993