
I26
lEEE
TRANSACTIONS
ON
ROBOTICS
AND
AUTOMATION,
VOL.
II,
NO.
I,
FEBRUARY
1995
Modeling
of
Slip
for
Wheeled Mobile Robots
R. Balakrishna and Ashitava Ghosal
Abstruct-
Wheeled Mobile Robots (WMRs) are known to
be
non-
holonomic systems, and most dynamic models of
WMRs
assume that
the wheels undergo rolling without slipping. This paper deals with the
problem of modeling and simulation of motion
of
a WMR when the
conditions for rolling are not satisfied at the wheels. We use a traction
model where the adhesion coefficient between the wheels of a WMR and
a hard flat surface is a function of the wheel slip. This traction model is
used in conjunction with the dynamic equations of motion to simulate the
motion of the WMR. The simulations show that controllers which do not
take into account wheel slip give poor tracking performance for the WMR
and path deviation is small only
for
large adhesion coefficients. This work
shows the importance of wheel slip and suggests
use
of accurate traction
models for improving tracking performance of a WMR.
Index
Terms-
Wheeled Mobile Robots, Slip, Modeling, Traction, Ad-
hesion.
I.
INTRODUCTION
Wheeled Mobile Robots (WMRs) are generally modeled
as
non-
holonomic dynamical systems with its wheels assumed to be rolling
without slipping. The formulation based on rolling without slip gives
kinematical mappings between wheel rotation and the position and
orientation of the WMR. However, rolling conditions are sometimes
violated in tractive maneuvering of WMRs, predominantly due to
slipping and scrubbing [3]. In this paper, we use
a
model for the
tractive force in terms of the adhesion coefficient, the linear and
angular velocity of the wheel. The dynamic equations of motion
are then derived including the effect of the tractive forces. It is
shown that the equations of motion reduce to that obtained for
'ideal' rolling when no slip conditions are used. The 'ideal' rolling
model is used to develop
a
model based controller. Simulation results
with
a PID
controller and the model based controller show that the
unmodeled slipping results in significant path deviation for the WMR,
especially when adhesion coefficients are small. Hence, to obtain
realistic models for maneuvering of WMRs, the rigid body dynamics
of the WMR needs to be used in conjunction with slipping and tractive
forces at the wheel-surface contact.
Previous work in wheeled mobile robot modeling have neglected
the aspect of wheel slip [I], [2], [19]. Other studies examined WMR
maneuvering by considering the case when the torque applied does
not exceed the traction limit [14]. The work presented by Alexander
and Maddocks [3] predicts the resulting motion of
a
WMR by
minimizing
a
friction functional when scrubbing takes place. Muir
and Neuman [ll], [12] describe methods to detect wheel slip and
describe corrective measures.
The modeling of tractive forces developed at the wheel has been
used for various studies [18], [4], [8]. The model presented here has
been widely used for automobile dynamic stability analysis [8], [17]
and for traction control [16]. We discuss the model for wheel slip
in Section
2.
Manuscript received
April
13, 1993; revised November 24, 1993.
The author is with the Department
of
Mechanical Engineering, Indian
IEEE
Log Number 94046
17.
Institute
of
Science, Bangalore 560 012 India.
The mechanical configuration of WMRs falls into one of two
categories
-
steered-wheeled vehicles and differential-drive vehicles.
This paper uses the latter category for simulation studies [9].
This paper is organized
as
follows: Section
2
presents the notion
of wheel slip and wheel dynamics, Section
3
presents the Adhesion
Coefficient model, Section 4 presents the WMR dynamic model with
the wheel slip incorporated and control of the WMR is considered
in Section
5.
In Section 6 simulations for
a
3
wheeled omni-wheeled
mobile robot is discussed and in Section 7 we present
our
conclusions.
11.
WHEEL-
SLIP
AND
SINGLE WHEEL DYNAMICS
For
a
conventional wheel, the linear velocity of the wheel center,
11,
and wheel angular velocity,
d,
are related through the expression,
1'
=
r
J,
where
r
is the wheel radius. This expression represents
'ideal' rolling. This relation is
a
nonholonomic constraint between
the variables
1,
and
J.
When the wheel rolls with slip this constraint
is violated.
To determine wheel slip between the wheel and
a
hard surface, it
is assumed that the surface does not deform during traction but the
wheel may undergo deformation at the contact patch. The wheel slip,
A,
can be defined
as
X
=(H
-
d*)
/I)
(1)
where,
d*
is defined
as
P/I.
with units of radsec, and
is
the wheel
angular velocity in,radsec. The value of
!/
is
d'
when
J*
>
H
and
is
i
when
J*
<
H.
It may be observed that
-1
5
X
5
1.
For
'ideal' rolling, when
d*
=
i,
the wheel slip
X
is zero. When the linear velocity is zero,
X
=
1,
and this represents the condition of wheel angular acceleration
and rolling in place. The skid condition is characterized by zero
angular velocity while the vehicle possesses
a
linear velocity. In this
case
X
=
-1.
To represent the combined effects of rolling and slipping, the
tractive forces of the wheel have to be introduced. The translational
and rotational dynamics of
a
wheel of radius
r,
mass
-\Itc,,
and
moment of inertia about the wheel center
.Itc,,
can be written
as
where,
Ft,
is the tractive force developed at the wheel contact,
.i:
and
H
are the linear and angular acceleration of the wheel center,
respectively, and
T
is the torque applied at the wheel axle. The above
equations of motion for
a
single wheel undergoing rolVslip motion
may be expressed in the state space form. Using the state vector,
x
=
{.I,
I
.
.1'2.
.r
1.
.I'
I
}
'
,
to represent the Cartesian position, linear
velocity, angular rotation and angular velocity, respectively, we can
write
(2)
as
or
compactly
as,
(3)
1
O42-296x/95$04.O0
0
1995
IEEE

IEEE
TRANSACTIONS
ON
ROBOTICS
AND
AUTOMATION.
VOL.
II,
NO.
I,
FEBRUARY
199.5
It can be observed that the translational and rotational dynamics for
a wheel undergoing rolVslip motion are coupled through the tractive
force
Ft.
It should be noted that the torque,
T,
is the only external
independent input to this dynamical system.
For this system to be locally controllable (see Isidori
[lo],
Spong and Vidyasagar
[15]),
the following vectors
{g.
ud~(g).
nd$.(y).
-
,td';,((/)}
~
should be linearly independent.'
One can show that
trd:
(g)
becomes a zero vector if
Ft
is constant.
Hence for the vectors
to
be linearly independent, the tractive force
Ft
should be at least a
C'
continuous function in
.I'.L
and
.VI,
which
are the linear and angular velocities of the wheel. In the next
section a traction model including the effects of wheel roll/slip
will be described.
111. ADHESION COEFFICIENT MODEL
The adhesion coefficient [I61 has also been referred to as the
"friction coefficient" for wheel rolling
[SI,
and generally used as a
measure to determine the adhesivity or sticking between two surfaces.
The tractive force,
Ft,
is generally obtained by the product of the
adhesion coefficient and normal force at the point of contact. The
adhesion coefficient is a function of the wheel dynamics and tractive
conditions. It depends on quantities such as linear velocity of the
wheel, the angular velocity of the wheel and the surface roughness
in qualitative and quantitative aspects. Various models have been
proposed for the tractive force,
Ff,
in literature [4], 1181,
[8].
Unruh
[I81 uses a model where the adhesion coefficient is assumed to be
constant while Allen and O'Massey [4] assume a model where the
adhesion coefficient is a function of the linear velocity. These models
are useful only when the wheel is locked and the vehicle is skidding.
We have used the traction model as proposed by Dugoff
et
al.
[8].
The models presented here are for longitudinal wheel traction force.
Adhesion CoefJicient Dependent on
Wheel
Slip
In the model proposed by Dugoff
et
al.
181,
the tractive force,
Ft,
is a function of wheel slip, A(see Section
2).
The tractive force,
Ft,
is given by
/trfAY,
where
p,
is the adhesion coefficient and
S
is the
normal reaction.
11.
depends on the wheel slip,
A,
which in
tum
is
a function of linear and angular velocities of the wheel. The tractive
force developed is then formulated as
Ft
=
I/
(A)
S
(4)
The relation between the adhesion coefficient,
pn,
and wheel slip,
A,
depends on the nature of the surface and the wheel material [8].
A
typical relationship is shown in Fig.
1
which shows the change
in adhesion coefficient,
p
",
for acceleration and braking conditions.
This curve has been proposed and verified by Dugoff
et
al.
[8].
For a given surface and wheel material, it has been observed that
though the quantitative characteristic of the curve may change, it
matches qualitatively for different surfaces. Of particular significance
is the peak value
pnppOk
(shown in Fig.
I),
which is present for the
acceleration and braking regions, with
A
taking positive and negative
values, respectively.
The adhesion coefficient,
pr,,
shows a rise and then a fall with
increasing wheel-slip,
A,
where
0
5
1x1
5
1.
The stable region is
represented by the portion of the curve that shows an increase in the
/tn
with increase in
A.
In this portion, the tractive forces that can
be sustained increases with the wheel-slip due to the increase in
p,
.
The fall of
p,,
beyond the peak
pop(,,l.
results in instability since the
tractive force reduces with increasing slip [16].
'trtl,
(!/)
-
denotes the Lie Bracket
of
the
two
vector fields
f
&
tj
with
--
-
tti/:.(y)
=
[.f.r,tl~--
I((/)]
-
and
iid';.($
=
-
0.
~
- -
-
c
c
0,
.-
-1.00
Fig.
1.
it
versus
X
curve.
I
-E
E
I
I
Fig.
2.
An Omni-wheel.
It was observed in Section
2,
that the controllability of a wheel is
ensured if the tractive force model,
Ff,
is at least
C1
continuous in
.1'2
and
.I'
I.
The present adhesion coefficient model based on wheel-slip
satisfies this criterion and also enables the representation of combined
rolling and slipping in the wheel. In view of the above mentioned
factors this adhesion coefficient model was used in the simulations.
The lateral tractive force model for the wheel is not considered
here, because the WMR considered in this work is a differential drive
vehicle with omni-wheels. However, lateral tractive force can also be
considered along similar lines [8], [17].
IV. WMR DYNAMIC MODEL
WITH
WHEEL SLIP
The omni-wheel has freely rotating barrels at the periphery and the
axis of rotation of the barrels are at an angle to the axis of rotation
of the wheel. Thus, they have two degrees of freedom as opposed
to conventional wheels which have one degree of freedom
[I],
11
11.
We consider a planar WMR with three omni-wheels and with barrels
inclined at 90" to the wheel axis [9]. To ensure that the wheel always
has two degrees of freedom, we consider a wheel having two layers
of barrels as shown in Fig.
2.
The kinematic and dynamics of WMRs
(assuming no slip) with more than three wheels and with barrels
inclined at other angles can also be derived
[I],
[2].
For the planar WMR with three omni-wheels placed at an angular
separation of 120", shown
in
Fig.
3,
one can find the relationship
between the wheel variables and the Cartesian variables by using
the no slip condition at the three wheels. Let the wheel rotational
speeds,
{HI.
H?.
4.1
},
be denoted by
i,
the wheel sliding speeds,

I
zn
IEEE TRANSACTIONS ON ROBOTICS AND AUTOMATION,
VOL.
I
I,
NO.
I,
FEBRUARY
1995
xG
x3
Fig.
3.
WMR
with
coordinate
frames
and forces
{ml.
(TZ.
m~},
be denoted by
E.
Since the motion of the WMR is in
a plane, the velocity of any point
G'
(origin of the body fixed frame
{G'})
on the WMR, with respect to a fixed coordinate system, can
be described by two components,
{
1.1
.
1
L
},
and the angular velocity
of the WMR can be described by a single component
\E
normal to
the platform. It may be noted that
{I
.
I
2
},
as shown in Fig.
3,
are
along
-Yc;f
and
I;;(
axes, respectively. We denote
{I
-1.
I
>.
g}
by
-
I?.
It can be shown
[l],
that
f
and the Cartesian variables,
E,
are
related by
where,
r
is the omni-wheel radius and
L,.
i
=
1.2.3 are the
distances of the omni-wheel contact point from
G'.
The
[
R
]
matrix
relates
f
and
and is analogous to Jacobian matrix in manipulators.
The relationship between the sliding velocity of the omni-wheels,
CJ,
and the Cartesian velocities has been presented by
Agullo
er
al.
[l].
When the platform is rolling without slipping it has
3
degrees
of
freedom. However, when the rolling constraint is not satisfied, the
WMR system has six degrees of freedom described by
{
I-,
@
}
and {HI.
Ha.
H:T}. This is because the
0's
and
1-1.
I
>.
Q
are not
related through the kinematic relations for 'ideal' rolling shown in
(5).
Let
C:
be the center of mass of the WMR. The frame
{G}
is
aligned to the frame
{
G'
}
and has coordinates
(P
I.
p.2
)
with respect
to
{
G'
}
as shown in Fig.
3.
The velocity of the center
of
mass, with
respect to a fixed frame, can be written as
(6)
=
{I;
-
%
Pa.
I,
+
%
PI
}'I.
Let
-U,,
be the mass of the WMR,
I,,
be the moment
of
inertia
of
the WMR about
2
axis,
I,
the moment of inertia of each wheel about
its axis, and
t'
the radius
of
each omni-wheel. The kinetic energy of
the WMR is given by the wheel rotational energy, and the WMR
translational and rotational energies. The kinetic energy contribution
of the barrels on the omni-wheel are neglected. The Lagrangian
for
the WMR is given as
Using the Lagrangian formulation, we can derive the equations of
motion
for
WMR systems as
${%}-%
=F,.
,j
=1
.....
G
where,
C,
is the Lagrangian
of
the WMR given in
(7),
qt.
i
=
1.
....
G
is the set
{
S.
I-.
\E.
HI
.
$2.
0.r
}
of generalized coordinates, and
;F
are the generalized forces.
The generalized forces corresponding to
0,.
i
=
1.2.3
are
T,
-
FtLr,
i
=
1.2.3 (see
(3)).
To obtain the generalized forces
for
(X.
I-.
9),
we have to write the
Ft,.
i
=
1.2.3 acting at the
wheels along the Cartesian degrees
of
freedom. This can be done by
use of the matrix
[
R
1''
[2].
Hence the six generalized forces can
be written as
;F={t.[R]'
(F1,.Fl,.Fl,)".~I
-Ft,t..
TJ-F~,~.
r:<-Ff3t*}.
(9)
The dynamic equations
of
motion
for
the WMR, including the
effects of wheel slip, can be written as shown at the bottom of this
page
or
compactly,
It may be noted that to arrive at the above equations, we have taken
{
G}
and
{
G'
}
to
be coinciding, i.e., el
=
PZ
=
0,
I
-1
=
PI,
1-2
=
62
and
LI
=
LZ
=
L.3
=
L.
It may be noted that the term
%
[
I)
]
1
arises because
I
-1
and
I
are components along the moving
-Y(;,
and
I;;!
axes and not along axis of the fixed coordinate system.
We can make the following observations from the dynamic equa-
tions of motion.
The individual wheel dynamics are coupled with the WMR
dynamics through the tractive forces. The ideal rolling condition
is not used.
The only input to this model of the WMR are the wheel torques,
T,.i
=
1.2.3.
The above equations of motion can be reduced to the equations
of motion derived using the no slip conditions. This is shown
below.

IEEE
TRANSACTIONS
ON
ROBOTICS
AND
AUTOMATION,
VOL.
11,
NO.
I,
FEBRUARY
1995
I29
The wheel dynamics alone are given by
(1
1). Multiplying
(1 1)
by
[RI'
[I]B+[.\f]li+\ir[C)]1=[R]'1.
(12)
The no-slip condition is given as
i,=
[
R
]
1.
Since
[
R
]
is a
constant matrix, we obtain,
=
[
R
]
1,
and on substituting them in
(I
2) and rearranging, we recover the WMR ideal dynamic equations
(see Agullo
et al.
[2]).
(13)
[
R
]
,
and substituting for
r
[
R
]
&,
from
(IO),
we get
[:\I*]
li
+
6
[
C)
]
1
=
[
R
]
where
[.\I*]
=
([MI
+
[
R
1"'
[I]
[
R
I).
rolling equations.
In this reduced order form, these equations are referred to as 'ideal'
V.
CONTROL
OF
THE
WMR
The control problem for the WMR may be defined as that of
guiding the WMR through a desired Cartesian path with specified
terminal points. In this section, the path tracking performance of the
WMR under PID control and a model based control using Cartesian
space feedback is discussed. The Cartesian space feedback may be ob-
tained either through dead reckoning
or
referential methods
[6].
The
dead reckoning method uses on-board sensors to estimate the current
position of the WMR. In the present case, we assume that there are
on-board sensors such as wheel encoders and accelerometers.
PID Control
This control scheme uses the Cartesian space errors to compute the
wheel torques according to the following PID control law
-
F
=
Zi,.
(Xd-X)+Ii,,
(Xd-X)+Ii,
where
X
denotes the vector
(S,
I-.
9)'
and
Xd
is the desired
Cartesian space path and
(
)
denotes the derivative with respect to
time.
The wheel torques,
r,
are related to the Cartesian force,
E,
and
are given
as
r=
[
RI'-'
E.
(15)
The dynamic model of the WMR is not used in this control scheme.
Model-Based Control
The model based control approach seeks to exploit the model
of
the system to be controlled to obtain enhanced performance. The
fundamental idea in this approach is to use the model of the system to
be controlled in the control law, such that the resulting error equation
is decoupled and linear, and is tunable by PID parameters
[7].
In this
section, we investigate the use
of
the dynamic equations of motion
derived using the condition of 'ideal' rolling,
(13)
in the model-
based control law. One possible rationale for using the 'ideal' rolling
model is that it is very hard to model adhesion coefficient and other
nonlinearities of the real system.
Assuming the availability of Cartesian space feedback and the
reduced order 'ideal' rolling model, a model-based control law can
be written as
-
T=ni
+
,I
where,
(1
=
[
R
I-'
,I
=
[
R
1-
'
{
\ir
[
C)
]
1
}
-
T'
=
X,/+
Ii,
(X</
-
XI
+
Zi,,(X,+
x
=
{S.
I-.
q/
where
[
M*
]
is given in
(13).
Error Dynamics
The error dynamics for the WMR undergoing rolling with slip
under the above model based control law is now presented. By
sub-
stituting the expression for
1,
(16).
in
(IO)
and
(1
1)
and rearranging,
we get
E,
+
Iia
E,
+
I<,,
E,
=
fc/(..
t)
(17)
where
E,
is the quantity
(X,I
-
X)
and
f,/(..t)=[-\I*]-' [RI' [I]H+r[R]' &([.\I*]-'
-[
JI
I-')
-
([
-\I*
I-'
-
[
.\I
I-')
C
(18)
where the quantities in the above equation are defined in Sections
4
and
5,
and
C
denotes
\ir[
C)
11.
We can consider the error equation as a linear system of second
order ordinary differential equation subjected to
a
disturbance f,,
(
. .
t
).
The first order representation of this system is given as
or
compactly as
Y
=
-[.4]Y
+
D(
..
t)
(19)
where,
Y
=
{Ev. Er}
'..
fi,,
and
fit.
are the positive definite gain
matrices, and
D(..
t)
=
{U.
f,j(
..
t)}"'
is the disturbance. It can be
assumed that
D(
..
t)
is bounded.
For
stability analysis, consider the
following Lyapunov function
(20)
v
=
1/2
Y"'
Y.
Differentiating with respect to time, we get
For
asymptotic stability
$
<
0,
and we require
i;
=
Y"'
Y
=
Y"
(-[.4]Y
+
D)
IlYll
>
ll[.41r1
DII.
(21)
The above condition implies that the ordinary differential equation
will be asymptotically stable if the state vector,
Y,
is
of sufficient
magnitude
(
greater than 11[.4]-'
011)
to ensure that
V
is negative.
Since
D(
.
.
t
)
is assumed to be bounded, the above equation suggests
that
llYll
is bounded and will approach
II[.-I]-'
Dll
as
t
tends to
infinity. The analysis also suggest a possible limit cycle behavior
since if
Y
<
II[.4]-'
Dll
then the system may be unstable. The
errors in WMR path tracking is clearly determined by the quantity
11[-4]-'
Dll,
and to reduce path deviation II[.4]-'
Dll
must be made
small. One way to make II[.4]-'
Dll
small is by choosing large
Zi,,
and
I<,.
which leads
us
to the (not surprising) conclusion that we
can expect better performance from our controller by using larger
gains. We can also reduce II[.4]-'
D
/I
by ensuring that
D(
..
t)
is
close to zero.
For
D(..t)
to be zero, we must have
-
F,
=
l/r
([A\I*]-'
-
[A\I]-')-' [E?']-'
.{([-\I*]-'
-
[AII]-l)
C
-
[.\I*]-'
[
R
1'
[I]
H}.
(22)
We can make the following observations from the above equation:
.
For
the disturbance
D(
..
t)
to be zero, a minimum tractive force
has to be developed ensuring rolling without slip. A higher
adhesion coefficient ensures larger resulting in less slipping of
the wheel and better Cartesian path tracking. This is observed
in the simulations.
Instances when the tractive force,
5,
generated is insufficient
may arise, resulting in a nonzero value for the disturbance,
D(..
t).
This is the cause of roll/slip motion at the wheel and
hence WMR path deviation.
I'
/
I30
1
:
pp
=
0.10
-
2:pp=tO.30
3:pp=+0.80
-
-
I
IEEE TRANSACTIONS ON ROBOTICS AND AUTOMATION, VOL.
I
I,
NO.
I,
FEBRUARY
1995
lime
(secs)
(a)
h
E
Z
Q,
3
U
Y
L
e
In general, the expression for
fd(
..
t)
may
also
contain extemal
forces acting on the WMR. In such
a
situation, the required
tractive force,
5,
is even larger and may not
be
sustained by
the wheel and surface. This may result in WMR path deviation.
This situation occurs during skidding.
From the above analysis, we can infer that for smaller WMR path
deviation we have to use higher gains or ensure sufficient tractive
force.
VI.
SIMULATION
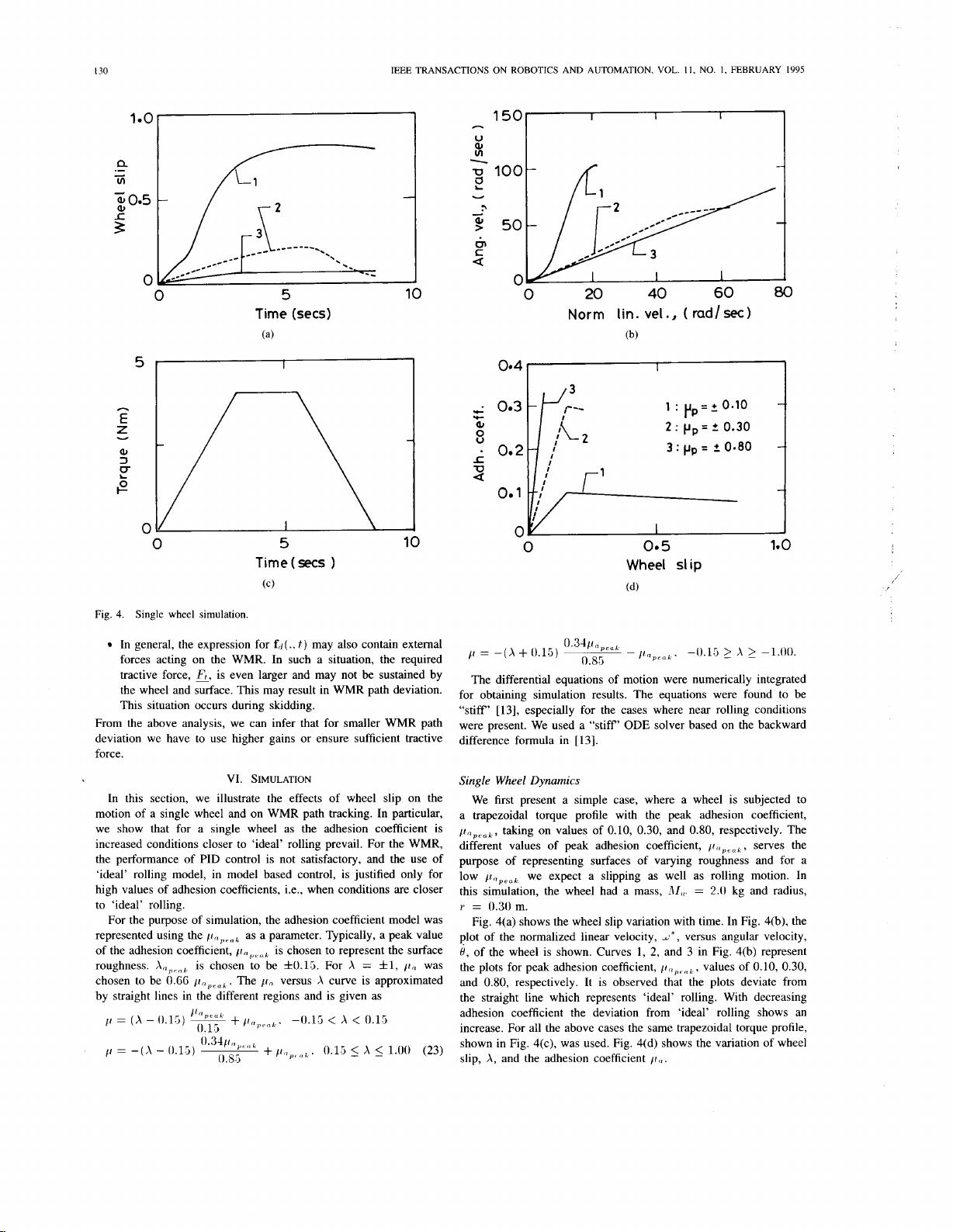
In this section, we illustrate the effects of wheel slip on the
motion of a single wheel and on WMR path tracking. In particular,
we show that for a single wheel
as
the adhesion coefficient is
increased conditions closer to ‘ideal’ rolling prevail. For the WMR,
the performance of
PID
control is not satisfactory, and the use of
‘ideal’ rolling model, in model based control, is justified only for
high values of adhesion coefficients, i.e., when conditions are closer
to ‘ideal’ rolling.
For the purpose of simulation, the adhesion coefficient model was
represented using the
pnpPnA
as
a
parameter. Typically,
a
peak value
of the adhesion coefficient,
pnpcul.
is chosen to represent the surface
roughness.
Xc,prnl.
is chosen to be f0.15. For
X
=
fl,
it,,
was
chosen to be
O.GG
pilpeal..
The
pn
versus
X
curve is approximated
by straight lines in the different regions and
is
given
as
I/
=
(A
-
0.15)
!!Ye!&
+
//<,,,,“,
.
-0.15
<
X
<
0.15
0.15
0.4
8
*
0.2
2
L
0.1
0
0
Norm
lin.
vel.,
(rad/=)
(b)
0.5
1.0
Wheel
slip
(4
Fig.
4.
Single wheel simulation.
-
//“pe*A.
-0.15
2
X
2
-1.00.
0’34/r“
peal.
//
=
-(A
+
0.15)
0.85
The differential equations of motion were numerically integrated
for obtaining simulation results. The equations were found to be
“stiff’ [13], especially for the cases where near rolling conditions
were present. We used
a
‘‘stiff’
ODE
solver based on the backward
difference formula in [13].
Single Wheel Dynamics
We first present
a
simple case, where
a
wheel is subjected to
a
trapezoidal torque profile with the peak adhesion coefficient,
pnpral,
taking on values of 0.10, 0.30, and 0.80, respectively. The
different values of peak adhesion coefficient,
p,jpcal.,
serves the
purpose of representing surfaces of varying roughness and for a
low we expect
a
slipping
as
well
as
rolling motion. In
this simulation, the wheel had a mass,
Jf8(
=
2.0
kg and radius,
I’
=
0.30
m.
Fig. 4(a) shows the wheel slip variation with time. In Fig. 4(b), the
plot of the normalized linear velocity,
I?*,
versus angular velocity,
4,
of the wheel is shown. Curves
1,
2,
and 3 in Fig. 4(b) represent
the plots for peak adhesion coefficient,
/rnpc,,l.,
values of 0.10, 0.30,
and 0.80, respectively. It is observed that the plots deviate from
the straight line which represents ‘ideal’ rolling. With decreasing
adhesion coefficient the deviation from ‘ideal’ rolling shows an
increase. For all the above cases the same trapezoidal torque profile,
shown in Fig. 4(c), was used. Fig. 4(d) shows the variation of wheel
slip,
A,
and the adhesion coefficient
p,,.