



read more






![Fig. 3. The centered B-splines forn = 0 to 4. The B-splines of degreen are supported in the interval[ ((n+1)=2); ((n+1)=2)]; asn increases, they flatten out and get more and more Gaussian-like.](/figures/fig-3-the-centered-b-splines-forn-0-to-4-the-b-splines-of-1u3hpmf0.png)
The subject is far from being closed and its importance is most likely to grow in the future with the ever-increasing trend of replacing analog systems by digital ones ; typical application areas are 582 PROCEEDINGS OF THE IEEE, VOL. Many of the results reviewed in this paper have a potential for being useful in practice because they allow for a realistic modeling of the acquisition process and offer much more flexibility than the traditional band-limited framework. Last, the authors believe that the general unifying view of sampling that has emerged during the past decade is beneficial because it offers a common framework for understanding—and hopefully improving—many techniques that have been traditionally studied by separate communities. Areas that may benefit from these developments are analog-to-digital conversion, signal and image processing, interpolation, computer graphics, imaging, finite elements, wavelets, and approximation theory.
Recent applications of generalized sampling include motion-compensated deinterlacing of televison images [11], [121], and super-resolution [107], [138].
Given the equidistant samples (or measurements) of a signal , the expansion coefficients areusually obtained through an appropriate digital prefiltering procedure (analysis filterbank) [54], [140], [146].
An interesting generalization of (9) is to consider generating functions instead of a single one; this corresponds to the finite element—or multiwavelet—framework.
The computational solution takes the form of a multivariate filterbank and is compatible with Papoulis’ theory in the special case .
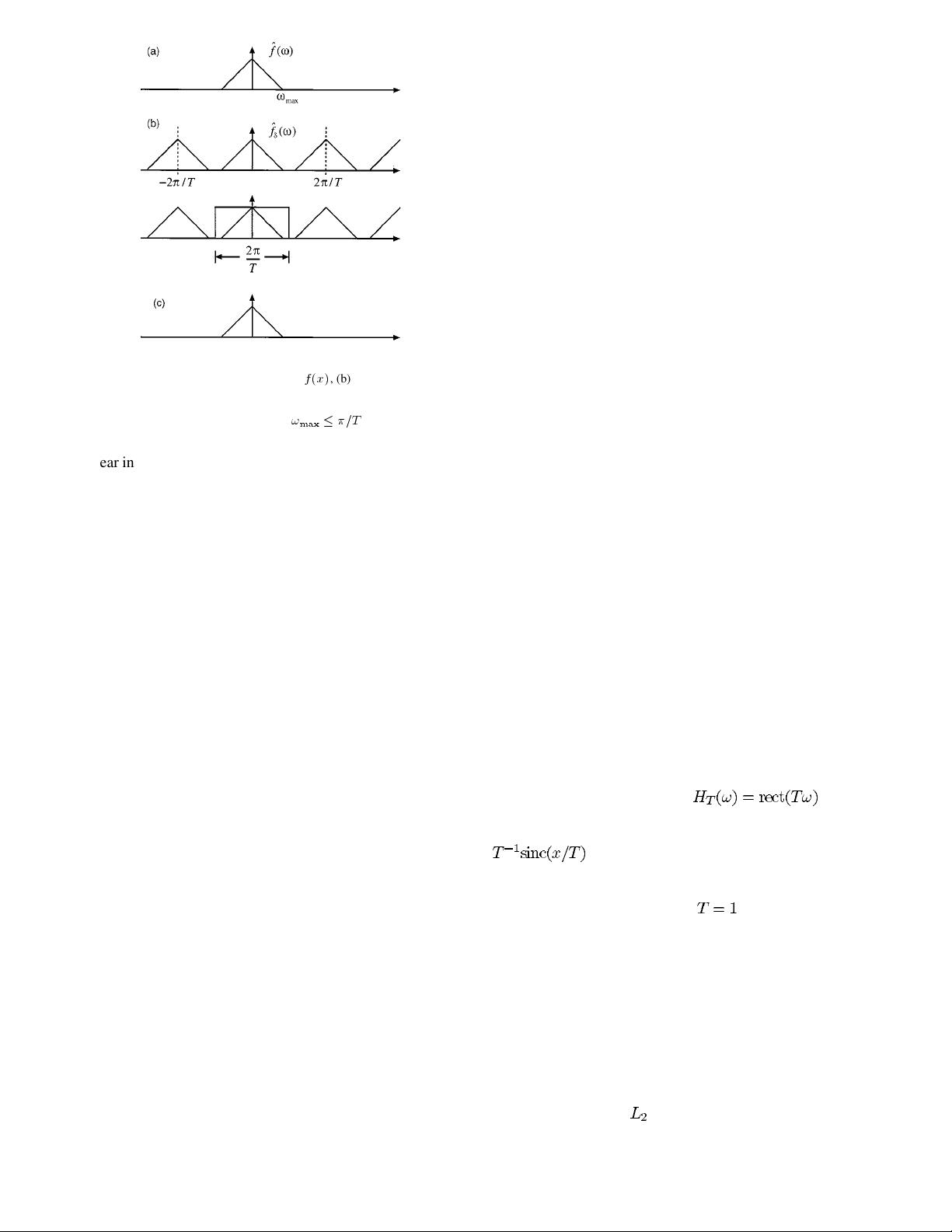
The projection interpretation of the sampling process that has just been presented has one big advantage: it does not require the band-limited hypothesis and is applicable for any function .
When this is not the case, the standard signal-processing practice is to apply a low-pass filter prior to sampling in order to suppress aliasing.
8. This graph clearly shows that, for signals that are predominantly low-pass (i.e., with a frequency content within the Nyquist band), the error tends to be smaller for higher order splines.
Having reinterpreted the sampling theorem from the more abstract perspective of Hilbert spaces and of projection operators, the authors can take the next logical step and generalize the approach to other classes of functions.
This has led researchers in signal processing, who wanted a simple way to determine the critical sampling step, to develop an accurate error estimation technique which is entirely Fourier-based [20], [21].
Note that the orthogonalized version plays a special role in the theory of the wavelet transform [81]; it is commonly represented by the symbol .
It is especially interesting to predict the loss of performance when an approximation algorithm such as (30) and (24) is used instead of the optimal least squares procedure (18).
The authors observe that a polynomial spline approximation of degree provides an asymptotic decay of 1 20 dB per decade, which is consistent with (45).