Progress In Electromagnetics Research B, Vol. 20, 147–166, 2010
THROUGH-THE-WALL DETECTION OF STATIONARY
HUMAN TARGETS USING DOPPLER RADAR
R. M. Narayanan, M. C. Shastry, P.-H. Chen, and M. Levi
The Pennsylvania State University
University Park, PA 16802, USA
Abstract—In homeland security and law enforcement situations, it is
often required to remotely detect human targets obscured by walls and
barriers. In particular, we are specifically interested in scenarios that
involve a human whose torso is stationary. We propose a technique to
detect and characterize activity associated with a stationary human in
through-the-wall scenarios using a Doppler radar system. The presence
of stationary humans is identified by detecting Doppler signatures
resulting from breathing, and movement of the human arm and wrist.
The irregular, transient, non-uniform, and non-stationary nature of
human activity presents a number of challenges in extracting and
classifying Doppler signatures from the signal. These are addressed
using bio-mechanical human arm movement models and the empirical
mode decomposition (EMD) algorithm for Doppler feature extraction.
Experimental results demonstrate the effectiveness of our approach to
extract Doppler signatures corresponding to human activity through
walls using a 750-MHz Doppler radar system.
1. INTRODUCTION
In recent years, there has been a great deal of research directed towards
the use of Doppler-radar systems for monitoring human activity.
Doppler-radar was first demonstrated for remotely monitoring human
activity in [1, 2]. SAR imaging and range detection [3–6] do not
work well to distinguish human targets from cluttered background.
In general, humans seldom stay still and their activities involve
considerable movement of their limbs. These movements are not always
captured by ranging systems. To recognize the presence of a human in a
target scene, it is desirable to look at the Doppler modulations of the
reflected waveforms, as these contain information about movements
Corresponding author: R. M. Narayanan (ram@engr.psu.edu).

148 Narayanan et al.
that are characteristic of human activity [7, 8]. Doppler detection
systems have the added advantages of simple design, low sampling
rates, and easy deployment. Indoor environments have minimal
Doppler clutter, which is highly desirable for effective detection.
Simple systems proposed in [2, 7, 9] for the detection of human
Doppler utilize time domain, frequency domain [9], and spectrogram
based approaches [7, 10]. The S-method is proposed in [11] for micro-
Doppler based characterization. Reassigned joint time-frequency
transforms are proposed in [12] for analysis. Existing systems for
human Doppler detection mostly deal with gross movement of the
human torso. In this paper, we consider detection and characterization
of Doppler from stationary humans, i.e., wherein the human torso
is not moving. In such scenarios, it is essential to extract Doppler
from breathing and transient movements of the arm. In this respect,
existing approaches to human Doppler analysis are limited by the time-
frequency ambiguity, and the a priori choice of time-frequency bases,
which are characteristic of traditional time-frequency distributions.
The EMD-Hilbert spectrum (referred to hereafter as EMD-HS)
algorithm is a recent development in the field of time-frequency
analysis [13]. It involves adaptive decomposition of a signal into
constituent time-frequency components called intrinsic mode functions
(IMFs). Preliminary work on using the EMD-HS approach towards
human Doppler analysis was presented in [14]. We review the EMD-
HS algorithm in Section 2 and define the instantaneous frequency
of a signal. The detection of transient activities is often crucial
to the detection of stationary human targets in the environment.
The Doppler frequencies associated with human movement can be
considered to result from the movement of the torso, movement of
the limbs, swinging of the limbs, expansion and contraction of the
chest cavity, and the changes in the position of the limbs. Human
activity can be considered as a combination of one or many of these
movements, and each activity occurs over a different time scale. In
the most general case, significant challenges to Doppler detection arise
because there is no way of knowing about the specifics of the human
activity a priori. In Section 3, we propose a model for human activity,
and consider issues involving time-frequency analysis. Based on the
reasoning presented in Section 3, the criteria we choose to decide on
the time-frequency technique are — frequency resolution, ability to
resolve time-frequency components of low amplitude, non-linearity of
transformation and adaptive selection of time-scales. These properties
are satisfied by the EMD algorithm. In Section 4, we present the results
of experiments involving human Doppler.
There has been considerable work in the past in the field of remote

Progress In Electromagnetics Research B, Vol. 20, 2010 149
detection of respiration in human beings. The focus in earlier work
was on cooperative human targets, with the radar operating with
exact knowledge about the position of the target. These systems were
designed specifically for health monitoring.
In our system, we consider the problem of detecting human arm
movements for security applications, where the radar operator do es
not have the cooperation of the target. The novel contribution of
the present paper is the detection and characterization of Doppler
from stationary humans, i.e., wherein the human torso is not moving.
We believe this is the first paper to apply bio-mechanical models
of human movement to study transient Doppler modulations due to
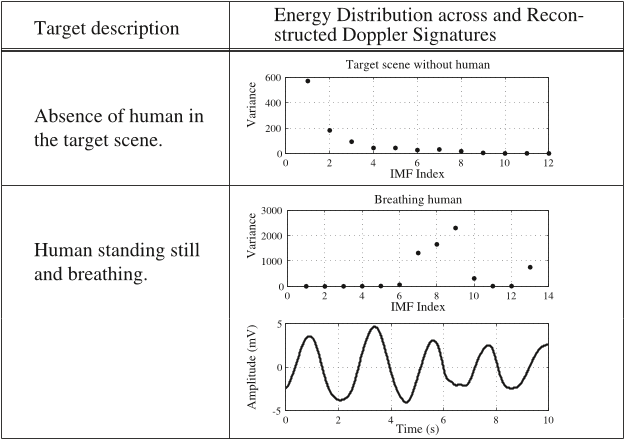
a stationary human. In Section 4, we show that our model for
human arm movement can predict Doppler signatures reasonably well
using the EMD algorithm. We present experimental results that
demonstrate distinct Doppler modulations that result from different
types of transient, non-repetitive human activity.
2. EMPIRICAL MODE DECOMPOSITION
2.1. Introduction to EMD-HS
The EMD-HS algorithm (also called the Hilbert Huang Transform
(HHT)) was proposed in [13] for analyzing non-stationary signals
originating from non-linear processes. EMD extracts intrinsic
oscillatory modes defined by the time scales of oscillation, called IMFs.
Such functions permit the application of the Hilbert transform and
the corresponding definition of instantaneous frequency in [13]. The
Hilbert transform yields the analytic version of the signal, from which,
the instantaneous frequency is extracted as shown in Equations (1)–
(3).
z(t) = x(t) + jH{x(t)} (1a)
= x(t) + jy(t) (1b)
= s(t)e
j
R
ω(t)dt
, (1c)
where
s(t) =
p
(x(t))
2
+ (y(t))
2
, (2)
ω(t) =
d arctan {y(t)/x(t)}
dt
. (3)
In Equation (1), H{} denotes the Hilbert transform. The functions s(t)
and ω(t) are the instantaneous amplitude and instantaneous frequency
of the signal, respectively.

150 Narayanan et al.
2.2. Sifting Process
The basic step of the EMD algorithm is the sifting process which
essentially extracts scales of the signal. Consider a signal with
P maxima and Q minima. The sifting process starts with
identifying the extrema of the signal, x(t), given by the set
S
1
max
= x
max
(t
1
), x
max
(t
2
), . . . , x
max
(t
j
), . . . , x
max
(t
P
) and S
1
min
=
x
min
(t
1
), x
min
(t
2
), . . . , x
min
(t
i
), . . . , x
min
(t
Q
). The points of set S
1
max
are interpolated to form the upper envelope of the signal, ˆx
max
.
Similarly, the points of the set S
1
min
are interpolated to form the
minimum envelope, ˆx
min
. The average envelope, (ˆx
max
+ ˆx
min
)/2 is
subtracted from the original signal x(t) resulting in the first iteration
of the sifting process, which is expressed as x
k
j
(t) where k denotes the
iteration (k = 1 for the first iteration). The iteration on k is continued
until the time-average hx
k
1
j
(t)i = 0 and the number of extrema of
x
k
1
j
is no more than one less than the number of zero-crossings. For
simplicity, we will drop the term k
1
and write the resulting function
as x
j
. The first sifting process produces the first IMF, with j = 1.
Following this, the function x
r
1
= x(t) − x
1
(t) is created, and the
sifting process is repeated, resulting in x
2
(t), the second IMF. The
IMFs are generated until the residue x
r
j
= x(t) −
P
n=j
n=1
x
j
(t). The
functions x
j
(t), j = 1, 2, . . . , N, exhaust x(t) and are nearly orthogonal
to one another. Since each IMF has only one extrema between any two
successive zero crossings, the frequency of the signal can be directly
inferred by measuring the temporal distribution of the zero crossings
of the signal. Further, the IMFs have symmetric envelop es, with the
difference between the number of extrema and the number of zero
crossings being no more than one. Owing to these characteristics, the
IMFs are referred to as being mono-component.
Since the residue is computed by successively subtracting the
sifted functions from the original signal, the EMD algorithm is data
driven and adaptive. Furthermore, the performance of the EMD
algorithm is sensitive to the interpolation procedure which results in
an inexact estimation of the envelope. The sifting process is defined for
continuous signals which means that the performance of EMD depends
on the sampling rate [15]. The dependence of the EMD algorithm
on these factors precludes a general, unique theoretical framework for
EMD. Defining a function space for the EMD algorithm is an ill-posed
problem, making it difficult to construct an analytical description of
EMD. However, empirically, the EMD has been shown to be effective in
extracting relevant components in a variety of applications involving
non-stationary signals. Its effectiveness has been demonstrated for

Progress In Electromagnetics Research B, Vol. 20, 2010 151
processing audio signals [16], global position systems [17], gravitational
waves [18], seismic signals [19], etc. While wavelet decomposition
decomposes a signal into components using predefined filter banks,
the EMD algorithm decomposes it into components whose mo des of
oscillations are adaptively decided by the nature of the signal.
In the absence of an analytical formulation, the performance of
the EMD algorithm is inferred from empirical observations. One of the
important properties of EMD is that it behaves like a dyadic filter for
a white noise input signal. The frequency of the IMFs resulting from
the decomposition of a white noise signal follows an exponential trend.
The first IMF represents the fastest modes of oscillation in the signal,
and with subsequent IMFs, the frequency, as measured by the number
of zero crossings decays exponentially as the index of the IMF. The
final IMF, always has just one zero crossing. From simulations, it was
found that the number of zero crossings in an intrinsic mode function is
proportional to e
−0.6n
, where n is the index of the IMF. Similarly, the
energy of the IMFs also reduces according to an exponential rule [20].
2.3. Hilbert Spectrum
Traditional time-frequency distributions define the frequency of a
signal based on the Fourier transform. This definition has the inherent
property of time-frequency uncertainty, as expressed by the lower
bound on the time-bandwidth product, ∆
t
∆
f
≥ 1/2. The analytic
signal corresponding to each IMF is constructed using the Hilbert
transform. The instantaneous frequency of this analytic signal is
defined as the derivative of the instantaneous phase defined in [13].
The different IMFs resulting from the EMD algorithm are orthogonal
to each other. The IMFs thus represent different time-scales of
oscillations, which form a set of basis functions. This implies that
there is no redundancy in the information contained in the different
IMFs. Using this property, a distribution is constructed from the
instantaneous frequencies of each of the IMFs. This distribution is
called the Hilbert spectrum (HS). Since the instantaneous frequency of
the EMD-HS approach is not defined based on the Fourier transform,
the time-frequency resolution is not limited by uncertainty. In our
implementation, we used a modified version of the code provided
in [21].