Durham Research Online
Deposited in DRO:
05 March 2015
Version of attached le:
Published Version
Peer-review status of attached le:
Peer-reviewed
Citation for published item:
Blair, Alexander and Kroukis, Aristeidis and Gidopoulos, N.I. (2015) 'A correction for the Hartree-Fock
density of states for jellium without screening.', Journal of chemical physics., 142 (8). 084116.
Further information on publisher's website:
http://dx.doi.org/10.1063/1.4909519
Publisher's copyright statement:
c
2015 American Institute of Physics. This article may be downloaded for personal use only. Any other use requires
prior permission of the author and the American Institute of Physics. The following article appeared in Journal of
Chemical Physics 142(8): 084116 (2015) and may be found at http://dx.doi.org/10.1063/1.4909519
Additional information:
Use policy
The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for
personal research or study, educational, or not-for-prot purposes provided that:
•
a full bibliographic reference is made to the original source
•
a link is made to the metadata record in DRO
•
the full-text is not changed in any way
The full-text must not be sold in any format or medium without the formal permission of the copyright holders.
Please consult the full DRO policy for further details.
Durham University Library, Stockton Road, Durham DH1 3LY, United Kingdom
Tel : +44 (0)191 334 3042 | Fax : +44 (0)191 334 2971
https://dro.dur.ac.uk

A correction for the Hartree-Fock density of states for jellium without screening
Alexander I. Blair, Aristeidis Kroukis, and Nikitas I. Gidopoulos
Citation: The Journal of Chemical Physics 142, 084116 (2015); doi: 10.1063/1.4909519
View online: http://dx.doi.org/10.1063/1.4909519
View Table of Contents: http://scitation.aip.org/content/aip/journal/jcp/142/8?ver=pdfcov
Published by the AIP Publishing
Articles you may be interested in
Finite-temperature second-order many-body perturbation and Hartree–Fock theories for one-dimensional
solids: An application to Peierls and charge-density-wave transitions in conjugated polymers
J. Chem. Phys. 140, 024702 (2014); 10.1063/1.4859257
Modeling the doubly excited state with time-dependent Hartree–Fock and density functional theories
J. Chem. Phys. 129, 204107 (2008); 10.1063/1.3020336
Real space Hartree-Fock configuration interaction method for complex lateral quantum dot molecules
J. Chem. Phys. 125, 034707 (2006); 10.1063/1.2219447
Accurate prediction of heat of formation by combining Hartree–Fock/density functional theory calculation with
linear regression correction approach
J. Chem. Phys. 121, 7086 (2004); 10.1063/1.1786582
Equilibrium geometries of low-lying isomers of some Li clusters, within Hartree–Fock theory plus bond order
or MP2 correlation corrections
J. Chem. Phys. 120, 11615 (2004); 10.1063/1.1729954
This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP:
129.234.252.67 On: Thu, 05 Mar 2015 16:00:06

THE JOURNAL OF CHEMICAL PHYSICS 142, 084116 (2015)
A correction for the Hartree-Fock density of states for jellium
without screening
Alexander I. Blair, Aristeidis Kroukis, and Nikitas I. Gidopoulos
Department of Physics, Durham University, South Road, Durham DH1 3LE, United Kingdom
(Received 14 December 2014; accepted 5 February 2015; published online 26 February 2015)
We revisit the Hartree-Fock (HF) calculation for the uniform electron gas, or jellium model, whose
predictions—divergent derivative of the energy dispersion relation and vanishing density of states
(DOS) at the Fermi level—are in qualitative disagreement with experimental evidence for simple
metals. Currently, this qualitative failure is attributed to the lack of screening in the HF equations.
Employing Slater’s hyper-Hartree-Fock (HHF) equations, derived variationally, to study the ground
state and the excited states of jellium, we find that the divergent derivative of the energy dispersion
relation and the zero in the DOS are still present, but shifted from the Fermi wavevector and energy
of jellium to the boundary between the set of variationally optimised and unoptimised HHF orbitals.
The location of this boundary is not fixed, but it can be chosen to lie at arbitrarily high values of
wavevector and energy, well clear from the Fermi level of jellium. We conclude that, rather than
the lack of screening in the HF equations, the well-known qualitative failure of the ground-state
HF approximation is an artifact of its nonlocal exchange operator. Other similar artifacts of the HF
nonlocal exchange operator, not associated with the lack of electronic correlation, are known in the
literature.
C
2015 AIP Publishing LLC. [http://dx.doi.org/10.1063/1.4909519]
INTRODUCTION
The uniform electron gas, or jellium model, is an arche-
typal example in solid-state physics and many-body theory.
Its treatment, in the Hartree Fock (HF) approximation, can
be found in classic textbooks,
1–6
where, we learn that the HF
equations applied to the ground state of the jellium admit
plane wave solutions with energy-wavevector dispersion rela-
tion given by
ε(k) =
k
2
2
−
k
F
π
*
,
1 +
k
2
F
− k
2
2k k
F
ln
k
F
+ k
k
F
− k
+
-
. (1)
k
F
is the Fermi wavevector, k
3
F
= 3π
2
(N/V). The single-
particle energy ε(k) is the sum of the free-electron energy,
k
2
/2, and the single-particle exchange energy. The Fermi
wavevector k
F
is often expressed in terms of the mean radius
per particle r
s
=
3
9π/4k
3
F
;
5
for typical values of r
s
in metals,
the two terms in (1) are comparable in size.
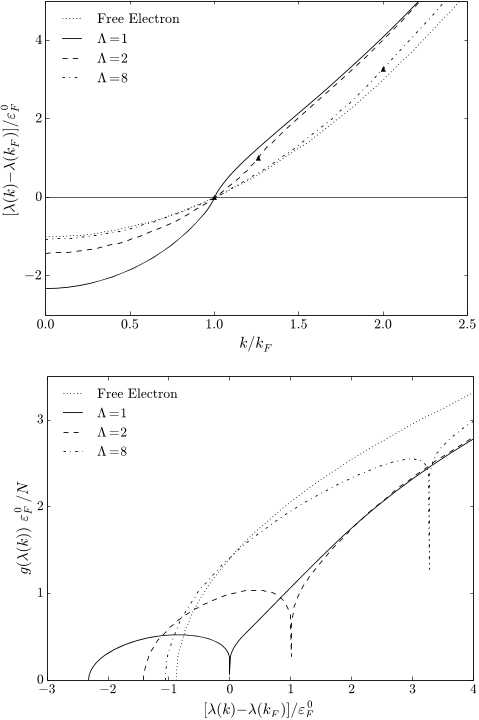
It is well known in the literature that the dispersion relation
(1) has a logarithmically divergent derivative at the Fermi
energy, shown in Fig. 1. Another marked difference between
the free electron result and the HF solution for jellium, evident
in Fig. 1, is the considerably increased bandwidth of the HF
dispersion. Finally, it is well known that in the HF approxi-
mation, the density of states (DOS) for jellium vanishes at the
Fermi level (Fig. 1), since the DOS is inversely proportional to
the derivative of the dispersion. The zero in the DOS at the
Fermi level suggests that jellium is a semimetal, in obvious
disagreement with experimental evidence for simple metals,
such as sodium or aluminium, which are described accurately
by the jellium model.
In the literature, the qualitatively wrong description of
jellium in the HF approximation is attributed to the long
range of the Coulomb repulsion.
1–6
It is well known that the
flawed description can be corrected by the introduction of
electronic many body correlation effects,
1–7
which screen the
bare Coulomb potential and thus eliminate the unphysical
divergent derivative of the dispersion relation, the zero in the
DOS at the Fermi level, and also reduce the bandwidth of the
HF dispersion relation of jellium.
In an effort to understand whether HF’s lack of screening
actually plays a role, we revisit the HF study of jellium, at-
tempting to correct the qualitative errors of the HF description,
but without including any form of electronic correlation. For
this purpose, we employ Slater’s hyper-HF (HHF) theory for
the ground and the excited states of an N-electron system.
8
Specifically, we use the single-particle HHF equations by Gi-
dopoulos and Theophilou,
9,10
who considered an N -electron
system described by a Hamiltonian H and then variationally
optimised the average energy
n
⟨Φ
n
|H|Φ
n
⟩ of all configura-
tions (N-electron Slater determinants Φ
n
) constructed from a
basis set of R spin-orbitals, R ≥ N.
THE HYPER-HARTREE-FOCK EQUATIONS
FOR JELLIUM
The aim in HHF theory is to obtain approximations, at the
HF level of description, for the ground and the excited states
of an N-electron system. These states are represented by N-
electron Slater determinants, constructed from a common set
of spin-orbitals. Obviously, to have the flexibility to describe
excited states, the number of spin-orbitals (R) must exceed
the number of electrons. For example, say we are interested
to approximate the ground and excited states of the helium
0021-9606/2015/142(8)/084116/5/$30.00 142, 084116-1 © 2015 AIP Publishing LLC
This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP:
129.234.252.67 On: Thu, 05 Mar 2015 16:00:06

084116-2 Blair, Kroukis, and Gidopoulos J. Chem. Phys. 142, 084116 (2015)
FIG. 1. Solid lines show ground-state HF results for jellium, compared to
free-electron results in dotted lines. (r
s
/a
0
= 4, ε
0
F
= k
2
F
/2.) Top: Energy
vs wave vector dispersion relation ε(k). The logarithmic divergence in the
derivative, dε/dk , is marked with a triangle (N). Bottom: DOS, showing the
unphysical zero at the Fermi level for jellium.
atom. In the HF ground state of He, the 1s orbital (ϕ
1s
) is
doubly occupied. To study a couple of excited states, we need
at least one more spin-orbital and the next one is ϕ
↑
2s
. With
the three available spin-orbitals, 1s
↑
,1s
↓
,2s
↑
, we can form
three configurations for the He atom (two-electron Slater deter-
minants): Φ
1
= [1s
↓
,1s
↑
], Φ
2
= [1s
↓
,2s
↑
], Φ
3
= [1s
↑
,2s
↑
]. In
HHF theory, we variationally optimise the three common spin-
orbitals simultaneously, by minimising the sum of the expec-
tation values
3
i=1
⟨Φ
i
|H|Φ
i
⟩. The minimisation leads to the
HHF single-particle equations for the three spin-orbitals. It
turns out that these equations resemble the ground-state HF
equations for the lithium atom (three electrons) but with a
weakened Coulomb repulsion between the three electrons, to
keep balance with the nuclear charge which has remained that
of the He nucleus.
In general, in HHF theory
8,9
for an N -electron system,
one considers a set of R orthonormal spin-orbitals, with R
≥ N. On this spin-orbital basis set one may define, D = R!/
(N !(R − N)!), N-electron Slater determinants.
The derivation of the single-particle HHF equations in
Ref. 9 is based on Theophilou’s variational principle,
11
D
n=1
⟨Φ
n
|H|Φ
n
⟩ ≥
D
n=1
E
(0)
n
, (2)
where {E
0
n
} are the D lowest eigenvalues of the N-electron
Hamiltonian H.
An extension of the variational principle, with unequal
weights in the sums in (2) was proposed by Theophilou,
12
and independently by Gross, Oliveira, and Kohn.
13
These vari-
ational principles can be derived as special cases from the
Helmholtz variational principle in statistical mechanics.
14,15
In
particular, the inequality in (2) arises as the high temperature
limit of the Helmholtz variational principle.
Optimisation of the R spin-orbitals {ϕ
i
} to minimise the
sum of the energies on the l.h.s. of (2) leads to the follow-
ing single-particle equations for the spatial part of the spin-
orbitals
9
(in atomic units):
−
1
2
∇
2
+ V
ext
(r)
ϕ
i
(r)
+
1
Λ
R
j=1
J
j
(r) − δ
s
j
, s
i
K
j
(r)
ϕ
i
(r) = λ
i
ϕ
i
(r), (3)
where,
Λ =
R − 1
N − 1
, (4)
and
J
j
(r)ϕ
i
(r) ≡
d
3
r
′
|
r − r
′
|
ϕ
j
(r
′
)
2
ϕ
i
(r), (5)
K
j
(r)ϕ
i
(r) ≡
d
3
r
′
|
r − r
′
|
ϕ
∗
j
(r
′
)ϕ
i
(r
′
)ϕ
j
(r) (6)
are the Coulomb and exchange operators, respectively. V
ext
sig-
nifies the attractive potential of the nuclear charge. For R = N,
Eq. (3) reduce to the familiar ground-state HF equations. In
Eq. (3), the orbitals ϕ
i
, with i = 1, . . . , R, are correctly repelled
electrostatically by a charge of N − 1 electrons. In contrast to
the ground-state HF case,
16
this holds true even for the orbitals
that are not occupied in the HHF ground-state Slater determi-
nant as long as these orbitals are variationally optimised, i.e.,
for ϕ
i
, with N < i ≤ R. Furthermore, the orbitals that are left
variationally unoptimised, i.e., ϕ
i
, with i > R, are repelled by
a charge of N − 1 + (1/Λ) electrons. In the HHF equations, the
well-known asymmetry in the treatment of the variationally
optimised and unoptimised orbitals by the nonlocal exchange
operator
16
is still present, but softened (for large Λ), compared
with ground-state HF. We note that for R > N, Koopmans’
theorem
19,20
ceases to hold for the HHF equations.
The HHF equations (3) have the form of ground-state
HF equations for a virtual system of R-electrons, where the
electronic Coulomb repulsion is multiplied by 1/Λ: 1/|r − r
′
|
→ Λ
−1
/|r − r
′
|. Therefore, the calculation of the optimal spin-
orbitals to represent the ground and excited-states of an N-
electron system in the HHF approximation is reduced to the
calculation of the ground-state HF orbitals of a fictitious sys-
tem with a greater number of electrons R ≥ N, and scaled
down electronic Coulomb repulsion. A related approach is the
“super-hamiltonian method” by Katriel.
22,23
Finally, before applying the HHF equations to jellium,
we remark that correlated, approximate eigenstates of the
Hamiltonian H can be obtained by diagonalising the matrix
⟨Φ
n
|H|Φ
m
⟩,
9
where Φ
n
are the N-electron HHF Slater deter-
minants. This configuration-interaction method employs the
HHF spin-orbitals, which are optimised to represent on equal
footing the ground and the excited states of H.
This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP:
129.234.252.67 On: Thu, 05 Mar 2015 16:00:06
084116-3 Blair, Kroukis, and Gidopoulos J. Chem. Phys. 142, 084116 (2015)
Solution of the HHF equations for jellium
Similarly to the HF ground state, the HHF equations for
jellium admit plane wave solutions. It follows that the ground-
state N-electron Slater determinant and its total energy are the
same in the HF and HHF approximations.
Although the HF and HHF equations for jellium admit
the same solution for the orbitals, the dispersion relations for
the single-particle energies ε(k) and λ(k) differ. In particular,
the HHF dispersion, λ(k), results from an optimisation that
involves a broader range of wavevectors than the HF dispersion
ε(k).
Following the standard treatment in textbooks,
1–6
it is
straightforward to work out directly the solution of the HHF
Eq. (3). Here, we exploit the similarity of Eq. (3) with ground-
state HF equations of an R-electron system, to obtain that the
HHF dispersion relation, λ(k), will be given by (1) with the
single-particle exchange energy scaled down by the factor 1/Λ,
λ(k) =
k
2
2
−
k
R
Λπ
*
,
1 +
k
2
R
− k
2
2k k
R
ln
k
R
+ k
k
R
− k
+
-
. (7)
k
R
is the Fermi wave vector of the virtual R-electron system,
k
3
R
= 3π
2
R
V
. (8)
Dividing k
R
/k
F
and taking the thermodynamic limit, N,
V → ∞, with the ratio Λ fixed, we obtain the following:
k
R
= Λ
1/3
k
F
. (9)
Substitution of the above into Eq. (7) yields the desired expres-
sion for the single particle energy levels of jellium, in terms
of Λ and the Fermi wavevector k
F
of the actual N-electron
system,
λ(k) =
k
2
2
− Λ
−2/3
k
F
π
×
(
1 +
Λ
2/3
k
2
F
− k
2
2Λ
1/3
k k
F
ln
Λ
1/3
k
F
+ k
Λ
1/3
k
F
− k
)
. (10)
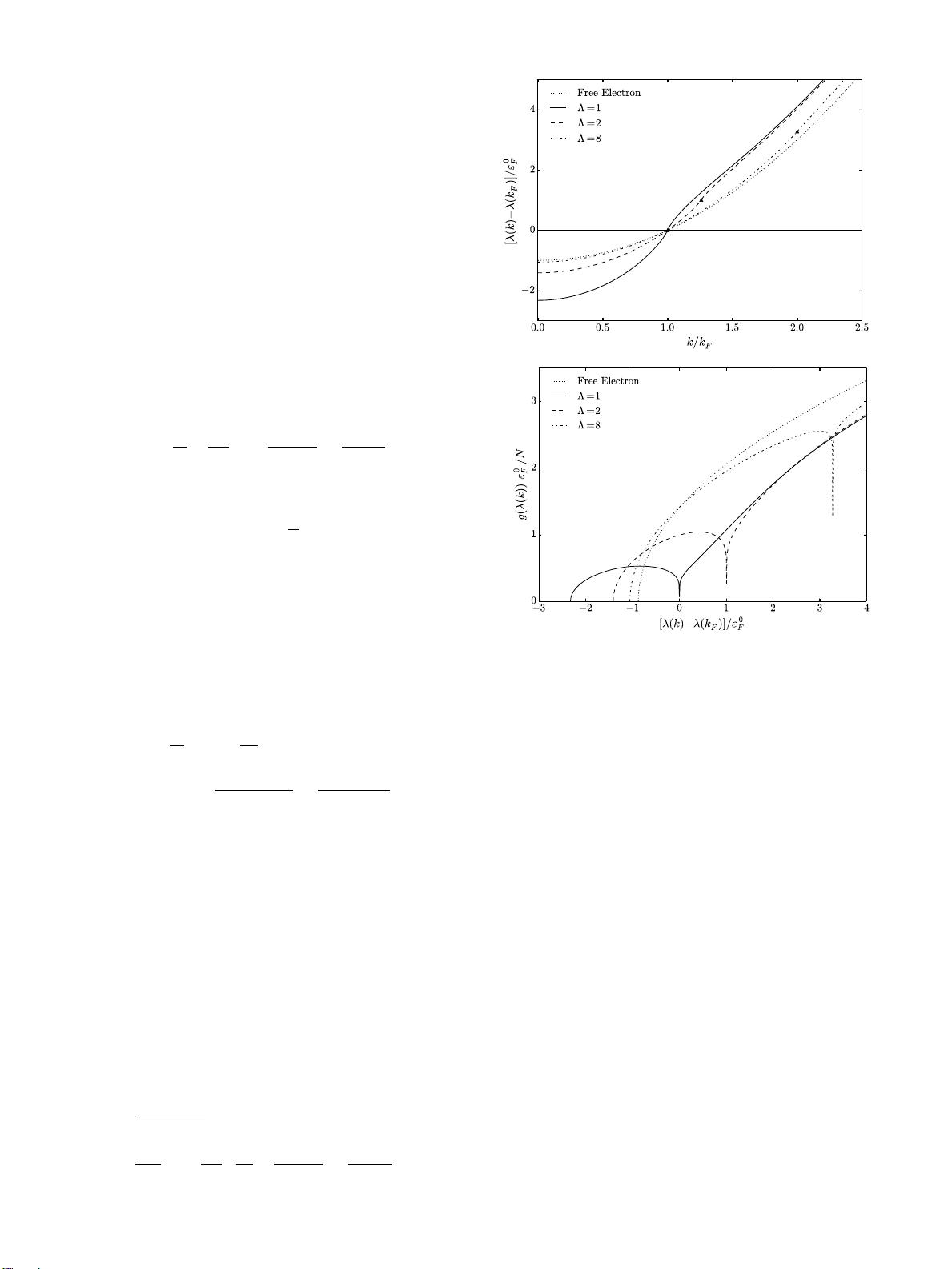
The dispersion relation in Eq. (10) reduces to the ground-state
Hartree-Fock result for Λ = 1, and to the free electron disper-
sion relation, λ(k) = k
2
/2, in the limit Λ → ∞ (see Fig. 2).
For increasing Λ, the bandwidth of the HHF dispersion, λ(k),
decreases compared to the ground-state HF dispersion, ε(k).
For Λ → ∞, the exchange term in HHF dispersion vanishes
and λ(k) reduces to the free-electron result.
Importantly, the wave vector at which the logarithmically
divergent derivative occurs is shifted from k
F
to k
R
, such that
the divergence no longer occurs at the Fermi energy of the
physical N-electron system, when the number of optimised
orbitals is R > N .
The DOS, g(λ)δλ, can be obtained directly from Eq. (10)
2
and is given by the parametric equation,
g(λ(k)) =
V k
2
π
2
(dλ/dk)
=
V k
2
π
2
k −
1
Λπ
*
,
k
R
k
−
k
2
R
+ k
2
2k
2
ln
k
R
+ k
k
R
− k
+
-
−1
.
(11)
FIG. 2. Excited-state HF results for jellium, for various Λ = R/N , compared
to free electron results (dotted lines). (r
s
/a
0
= 4, ε
0
F
= k
2
F
/2.) Top: Energy vs
wave vector dispersion relations λ(k). When Λ = 1, λ(k) = ε(k). Triangles (N)
mark logarithmic divergence in dλ/dk at Fermi level of fictitious R-electron
system. Bottom: DOS g (λ(k)), showing the zero at the Fermi level of the
fictitious R-electron system.
g(λ(k)) is expressed in terms of k
R
(rather than Λ
1/3
k
F
) to keep
the notation simple. For any finite Λ, the DOS still vanishes.
However, as shown in Fig. 2, the zero in the DOS occurs at the
Fermi energy of the fictitious R-electron system, λ(k
R
), rather
than the Fermi energy of the physical system λ(k
F
).
DISCUSSION
In metals, screening is an important effect that reduces the
range of the effective repulsion between electrons, shielding
any charge at distances greater than a characteristic screening
length. In the literature of many-body theory
1,3–6
and solid-
state physics,
2–4
where jellium is a paradigm, the qualitatively
flawed description of metals by the HF approximation is
attributed to the long-range nature of the Coulomb interaction,
which, combined with the neglect of correlation, deprives from
the HF equations the flexibility to model the phenomenon
of screening. This understanding of HF’s failure is further
supported by the softening of the divergence in the slope of
ε(k), after replacing the bare Coulomb potential in the HF
nonlocal exchange term by a screened Coulomb potential.
2
On the other hand, in the theoretical chemistry literature, it
is well known that the HF nonlocal exchange term, in finite sys-
tems, gives rise to several counterintuitive results, reminiscent
This article is copyrighted as indicated in the article. Reuse of AIP content is subject to the terms at: http://scitation.aip.org/termsconditions. Downloaded to IP:
129.234.252.67 On: Thu, 05 Mar 2015 16:00:06