HAL Id: hal-01164388
https://hal.archives-ouvertes.fr/hal-01164388
Submitted on 16 Jun 2015
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
A new analytical torque formula for axial eld
permanent magnets coupling
Bastien Dolisy, Smail Mezani, Thierry Lubin, Jean Lévêque
To cite this version:
Bastien Dolisy, Smail Mezani, Thierry Lubin, Jean Lévêque. A new analytical torque formula for axial
eld permanent magnets coupling. IEEE Transactions on Energy Conversion, Institute of Electrical
and Electronics Engineers, 2015, 8 p. �10.1109/TEC.2015.2424159�. �hal-01164388�

1
Abstract— In this paper, we present a simple and accurate
analytical expression to compute the torque of axial-field
magnetic couplings. The torque expression is obtained by solving
the three-dimensional (3D) Maxwell equations by the method of
separation of variables. Here we adopt the assumption of
linearization at the mean radius, the problem is then solved in 3D
Cartesian coordinate (we neglect the curvature effects). To show
the accuracy of the torque formula, the results are compared
with those obtained with 3D finite-element simulations, and
experimental tests. As the proposed formula needs very low
computational time and depends directly on the geometrical
parameters, it is used for a design optimization using
multiobjective genetic algorithms.
Index Terms— Genetic algorithms, magnetic coupling,
permanent magnets, torque transmission, 3D analytical model.
I. INTRODUCTION
agnetic couplings (or couplers) can transmit a torque
without mechanical contact. This is very interesting for
applications requiring isolation between two different
atmospheres. They can be used in the naval propulsion [1] for
torque transmission between motors and propellers, or in
chemical industry for health constraints. In addition, the
absence of mechanical contact increases the lifetime of the
system and reduces noise, vibrations and mechanical friction
losses. Moreover, it provides natural protection against
overloads.
Magnetic couplings can have axial or radial flux topologies
(Fig. 1). They both consist of two rotors, each of which is
composed of an array of permanent magnets alternately
magnetized along the θ-direction. The two rotors present the
same number of pole pairs (p=6 in Fig.1).
The axial-flux topology is studied in this paper. It consists of
two similar rotors facing each other. As shown in Fig. 2, the
air-gap between the two rotors is noted e.
The magnets are sector shaped with a thickness (along z-
direction) noted h for both rotors. The inner and outer radii are
respectively noted R
in
and R
out
.
The authors are with the Groupe de Recherche en Electrotechnique et
Electronique de Nancy, Université de Lorraine, 54506 Nancy, France (e-mail:
´ b-dolisy@hotmail.fr).
(a) Radial flux (b) Axial flux
Fig. 1 Topologies of rotating magnetic couplings (p=6).
The magnet angular opening to pole opening ratio is noted α
and varies between 0 and 1. The angular lag (load angle)
between the two rotors is noted φ.
The electromagnetic computation of magnetic couplings is
carried out using several methods. The Finite-element (FE)
method is so far the preferred method of analysis. Indeed, it
leads to accurate results taking into account the non-linearity
of magnetic materials and the actual coupler geometry [2-4].
The main drawback of FE methods is the long computation
time and the lack of flexibility. It is therefore unsuitable for
optimization purposes which require many repetitive
computations. In order to reduce the computation time,
analytical models can be developed by solving the partial
differential equations (PDE) arising from Maxwell’s
equations. It is necessary to make some assumptions regarding
the linearity of magnetic materials and geometry
simplification [5-9]. Usually, the problem is solved under a
two-dimensional (2D) approximation which, in some situation
like in axial field couplers, results in a 30% overestimation of
the torque compared to 3D FE prediction [10-12]. Three-
dimensional analytical models for magnetic couplings have
been proposed in the literature [6],[13] and [14]. Biot-Savart
like formulas are used to determine the magnetic field
distribution in ironless structures (magnets in free space).
The method of images could be used to consider infinitely
permeable iron walls but the computation time increases.
Recently, it has been shown that Fourier analysis can be used
to solve 3D problems with ferromagnetic parts [7].
A new analytical torque formula for axial field
permanent magnets coupling
B. Dolisy, S. Mezani, T. Lubin, J. Lévêque
M

2
Fig. 2 Dimension of the permanent magnets of an axial flux coupler topology
(iron yokes not shown).
In [5], the authors developed a 3D analytical model to
compute the no load flux in axial-field permanent magnet
synchronous machine. In this method (also called sub-domain
method), it is necessary to numerically solve an algebraic
system of linear equations to calculate the Fourier coefficients.
Hence, even keeping its analytical formalism, the “fully
analytical” meaning of the sub-domain method is somewhat
lost. Nevertheless, in terms of computation time, such a
method remains more efficient than a FE analysis.
In this paper, the sub-domain method is used to analytically
determine the magnetic field distribution in the axial magnetic
coupling shown in Fig. 1b. A new and purely analytical
expression for the torque evaluation is then derived from the
3D solution. The proposed torque formula, which depends
directly on the physical and geometrical parameters, is
obtained by solving the PDEs in 3D Cartesian coordinates by
assuming a linearized geometry at the mean radius (we neglect
the curvature effects). We also consider an infinite
permeability of the iron yokes.
The torque expression is obtained in two steps:
- Firstly, we only consider the magnets on one side of the
coupling (the magnets on the other rotor are turned off). Then,
we compute the magnetic field by using a magnetic scalar
potential formulation.
- Secondly, using the analogy between the electrostatic and the
magnetostatic fields, the magnetic force acting on the magnets
placed on the opposite side is obtained by using the equivalent
electrostatic Lorentz force.
To analyze the accuracy of the proposed torque formula, the
results are compared to those obtained from 3D finite-element
simulations and from experimental investigations. Finally, the
analytical formula is used for a genetic algorithm
multiobjective optimization of the coupler.
II. ANALYTICAL MODEL
As stated above, the torque expression will be derived using
the analogy that exists between the electrostatic and the
magnetostatic fields.
A. Magnetic force from the electrostatic-magnetostatic
analogy
For simplicity, let us consider, in free space, an electrostatic
uniform surface charge density
s
(C/m
2
), subjected to an
electric field
[16]. The Lorentz force (N) exerted on
s
is
(1)
where S is the surface which carries
s
.
From the magnetostatic point of view, it is usual to use an
equivalent magnetic surface charge
m
in A/m
[7],[11],[14],[15],[16]. Unlike
s
, the magnetic charge
m
doesn’t have any physical meaning. However, it is introduced
for modelling purposes in which it usefully replaces some
magnetic field sources (magnets, current carrying
solenoids,…).
The magnetic force (N) which is analogous to the electrosatic
one, given by (1), is then obtained by
(2)
Here, S is the surface which carries
m
.
The force expressions (1) and (2) show that the electrostatic-
magnetostatic analogy links the electric field
to the
field
(called flux density).
Concerning the studied magnetic coupler, all what we need to
compute the force is the magnet’s magnetic surface charge on
one rotor and the magnetic field created by the magnets of the
second rotor (the magnets on the first rotor are turned off).
Furthermore, expression (2) which uses Lorentz force in free
space gives, for our coupler, the right values of the force along
the x and y directions only (no other material than air in these
two direction). However, since ferromagnetic materials are
present in the z-direction, (2) will not give the right value of
the force and we have to use Maxwell stress tensor or virtual
work methods.
To deal with the presence of iron media an equivalent surface
charge of the ferromagnetic material could be introduced [15].
B. Magnetic field due the magnets of one rotor
The iron-yokes have an infinite permability. Hence, the
magnetic field is null in the iron parts.
The boundary condition on the iron interface is then
(3)
where
is the outward normal to the considered surface and
the magnetic field strength.
Rare-earth permanent magnets have a relative permeability
close to that of air (
).

3
The studied coupler doesn’t contain any current source. To
solve the magnetostatic problem, it is then more convenient to
use a magnetic scalar potential
formulation
(
). In the different media, the flux density
is given by
Air region:
Magnets region:
(4)
(5)
where
is the magnetization of the magnet.
To simplify the analysis, we make the assumption of
linearization at the mean radius, so the curvature effect is not
considered. However, this allows to solve the problem in a
Cartesian coordinates system, which is simpler than to solve
the problem in cylindrical coordinates where special functions
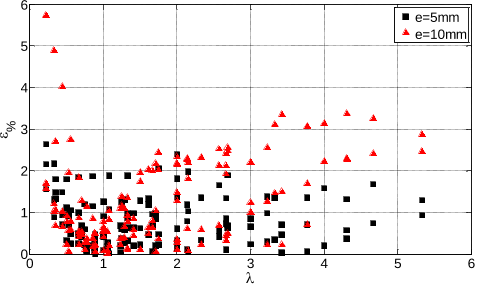
appear [5]. The validity of the linearized model is discussed
later in the paper.
Fig.3 shows the problem to solve after linearization. The main
dimensions of the linearized coupler are
Due to the alternate polarity along the x-direction, only one
pole is considered with anti-periodic boundary conditions
along x.
A second anti-periodic condition is applied at the external
boundaries on the y-coordinate. This condition is a fictitious
but a necessary one in order to get a solution. Nevertheless, by
setting
, this anti-periodic condition leads to
at
, which is of course a more realistic physical
condition (Usually,
allows to obtain accurate
results).
As stated above, the whole resolution domain contains magnet
and air regions, Fig.4.
Domain I () corresponds to the magnet region of
height h. The magnetization vector is noted
and it is obtained by expanding the magnetization into a
double Fourier series along x and y-directions (Fig. 5).
;
(7)
Fig. 3 Dimensions of one magnet pole after linearization (axis of rotation,
located at
not shown).
where n, m are odd integers and B
r
is the residual flux density
of the permanent magnets. Notice that the magnetization given
by (7) is divergence free
.
Domain II (
) is composed of the actual air-gap
and the second magnet (whose magnetization is turned off).
The magnetic scalar potential is noted
in domain I and
in domain II.
and
are the solution of Laplace
equation
(8)
Fig. 4 Domains and equations in the plan (x,z).
Fig. 5 Magnetization Mz as a function of x and y (domain I).
;
;
(6)

4
By considering the anti-periodic boundary conditions along
the x and y coordinates, the use of the method of separation of
variables leads to the following form solutions for
and
with
(9)
The coefficients A
I
, B
I
, A
II
and B
II
are obtained using the
interface and boundary conditions.
The Boundary condition in domains I and II are set at z=0 and
z=h
t
, respectively. These conditions state that the tangential
magnetic field components H
x
and H
y
are zero (iron
boundaries). This leads to
(10)
Interface conditions between domains I and II are set at z=h.
Domain I and II have the same magnetic permeability (µ
r
=1),
so the normal flux density (B
z
) and the tangential magnetic
fields (H
x
and H
y
) of the domain I and II will be equal at z=h.
The two following expressions arise
(11)
Finally, the coefficients A
I
, B
I
, A
II
and B
II
are calculated by
solving an algebraic system of linear equations arising from
(10) and (11). They are given by
(12)
C. Equivalent surface charge density of the second PM rotor
The equivalent surface charge density of a magnet
(Coulombian model) with uniform magnetization is given by
(13)
Where
is the magnetization vector and
represents the outward normal to the considered surface.
This dot product has to be performed on all the external
surfaces of the magnet volume.
Fig.6 shows a rectangular permanent magnet with a uniform
magnetization in the z-direction. From (13), the magnet is
then represented by two surface charge densities
+
and
-
.
In our problem, the surface charge density
is located
at
and the surface charge density
at
.
D. Torque expression
The force is computed using (2) where the integration is
performed on the surfaces carrying
and
. However,
according to the boundary condition (3), the tangential
components
and
of the flux density are null on the
charged surface
(at
), so the forces that contribute to
torque (F
x
and F
y
) also vanishes. Hence, the integation is only
performed on the charged surface
(at ).
The axis of rotation (the shaft axis) is parallel to the Oz axis.
This axis has constant coordinates noted (x
0
,y
0
) in the (Oxyz)
reference frame. The z-component of the torque is then
obtained by
(14)
The variable
in (14) corresponds, in cartesian coordinates,
to the angular lag (load angle) between the two rotors of the
coupling.
and are related by
.
Notice that the maximum (pull-out) torque is obtained for a
position
Fig. 6 Equivalent surface charge density for a rectangular permanent magnet.
![Fig. 7 Axial flux magnetic coupling prototype [11],[12].](/figures/fig-7-axial-flux-magnetic-coupling-prototype-11-12-4zwb9g07.png)

![TABLE I DIMENSIONS OF THE CONSTRUCTED MAGNETIC COUPLING [11],[12]](/figures/table-i-dimensions-of-the-constructed-magnetic-coupling-11-6cs62iwn.png)