Asymptotic solvers for ordinary
differential equations with multiple
frequencies
Marissa CONDON
School of Electronic Engineering, Dublin City University
E-mail: marissa.condon@dcu.ie
Alfredo DEA
˜
NO
Depto.de Matem´aticas, Universidad Carlos III de Madrid
E-mail: alfredo.deanho@uc3m.es
Jing GAO
∗
School of Mathematics and Statistics, Xi’an Jiaotong University
E-mail: jgao@mail.xjtu.edu.cn
Arieh ISERLES
DAMTP, Centre for Mathematical Sciences, University of Cambridge
E-mail: A.Iserles@damtp.cam.ac.uk
Abstract
We construct asymptotic expansions for ordinary differential equa-
tions with highly oscillatory forcing terms, focussing on the case of
multiple, non-commensurate frequencies. We derive an asymptotic ex-
pansion in inverse powers of the oscillatory parameter and use its trun-
cation as an exceedingly effective means to discretize the differential
equation in question. Numerical examples illustrate the effectiveness
of the method.
Mathematics Subject Classification: 65L05,65D30,42B20,42A10
∗
Communicating author
1

1 Introduction
Our concern in this paper is with the numerical solution of highly oscil-
latory ordinary differential equations of the form
y
0
(t) = f(y(t)) +
M
X
m=1
a
m
(t)e
iω
m
t
, t ≥ 0, y(0) = y
0
∈ C
d
, (1.1)
where f : C
d
→ C
d
and a
1
, ··· , a
M
: R
+
→ C
d
are analytic and ω
1
, ω
2
, ··· , ω
M
∈
R \ {0} are given frequencies. We assume that at least some of these fre-
quencies are large, thereby causing the solution to oscillate and rendering
numerical discretization of (1.1) by classical methods expensive and ineffi-
cient. Many phenomena in engineer and physics are described by the oscil-
latoryly differential equations(Chedjou2001, Fodjouong2007, Slight2008 and
so on).
A special case of (1.1) with ω
2m−1
= mω, ω
2m
= −mω, m = 0, 1, ··· , bM/2c,
where ω 1, is a special case of
y
0
(t) = f(y(t)) + G(y)
∞
X
k=−∞
b
k
(t)e
ikωt
, t ≥ 0, y(0) = y
0
∈ C
d
, (1.2)
where G : C
d
× C
d
→ C
d
is smooth, which has been already analysed at
some length in (Condon, Dea˜no and Iserles 2010). It has been proved that
the solution of (1.2) can be expanded asymptotically in ω
−1
,
y(t) ∼ p
0,0
(t) +
∞
X
r=1
1
ω
r
∞
X
m=−∞
p
r,m
(t)e
imωt
, t ≥ 0, (1.3)
where the functions p
r,m
, which are independent of ω, can be derived recur-
sively: p
r,0
by solving a non-oscillatory ODE and p
r,m
, m 6= 0, by recursion.
An alternative approach, based upon the Heterogeneous Multiscale Method
(E and Engquist 2003), is due to Sanz-Serna (2009). Although the theory
in (Sanz-Serna 2009) is presented for a specific equation, it can be extended
in a fairly transparent manner to (1.2) and, indeed, to (1.1). It produces
the solution in the form
y(t) ∼
∞
X
m=−∞
κ
m
(t)e
imωt
, (1.4)
2

where κ
m
(t) = O(ω
−1
), m ∈ Z.
1
Formally, (1.3) and (1.4) are linked by
κ
m
(t) =
∞
P
r=0
1
ω
r
p
r,0
(t), m = 0,
∞
P
r=1
1
ω
r
p
r,m
(t), m 6= 0.
We adopt here the approach of (Condon et al. 2010), because it allows us
to derive the expansion in a more explicit form.
The highly oscillatory term in (1.2) is periodic in tω: the main difference
with our model (1.1) is that we allow the more general setting of almost
periodic terms (Besicovitch 1932). It is justified by important applications,
not least in the modelling of nonlinear circuits (Giannini and Leuzzi 2004,
Ram´ırez, Su´arez, Lizarraga and Collantes 2010).
Another difference is that we allow in (1.1) only a finite number of dis-
tinct frequencies in the forcing term. This is intended to prevent the oc-
currence of small denominators, familiar from asymptotic theory (Verhulst
1990). Note that (Chartier, Murua and Sanz-Serna 2012) (cf. also (Chartier,
Murua and Sanz-Serna 2010)) employs similar formalism - a finite number
of multiple, noncommensurate frequencies - except that it does so within
the ‘body’ of the differential operator, rather than in the forcing term.
We commence our analysis by letting U
0
= {1, 2, ··· , M} and ω
j
= κ
j
ω,
j = 1, ··· , M, where ω is a large number which will serve as our asymptotic
parameter. Consequently, we can rewrite (1.1) in a form that emphasises
the similarities and identifies the differences with (1.2),
y
0
(t) = f(y(t)) +
X
m∈U
0
a
m
(t)e
iκ
m
ωt
, t ≥ 0, y(0) = y
0
∈ C
d
, (1.5)
Section 2 is devoted to a ‘warm up exercise’, an asymptotic expansion of a
linear version of (1.5), namely
y
0
(t) = Ay(t) +
X
m∈U
0
a
m
(t)e
iκ
m
ωt
, t ≥ 0, y(0) = y
0
∈ C
d
, (1.6)
where A is a d × d matrix. Of course, the solution of (1.5) can be written
explicitly, but this provides little insight into the real size of different com-
ponents. The asymptotic expansion is considerably more illuminating, as
1
In the special case considered in (Sanz-Serna 2009) it is true that κ
m
(t) = O (ω
−|m|
),
m ∈ Z, but this does not generalise to (1.2).
3

well as hinting at the general pattern which we might expect once we turn
our gaze to the nonlinear equation (1.5).
For the ODE with the highly oscillatory forcing terms with multiple
frequencies, the asymptotic method is superior to the standard numerical
methods. With less computational expense, this asymptotic method can
obtain the higher accuracy. Especially, the asymptotic expansion with a
fixed number of terms becomes more accurate when increasing the oscillator
parameter ω.
In Section 3 we will demonstrate the existence of sets
U
0
⊆ U
1
⊆ U
2
⊆ ···
and of a mapping
σ :
∞
[
r=0
U
r
→ R
such that the solution of (1.5) can be written in the form
y(t) ∼ p
0,0
(t) +
∞
X
r=1
1
ω
r
X
m∈U
r
p
r,m
(t)e
iσ
m
ωt
, t ≥ 0. (1.7)
As can be expected, the original parameters {κ
1
, κ
2
, ··· , κ
M
} form a subset
of U
r
. However, we will see in the sequel that the set σ(U
r
) is substantially
larger for r ≥ 3. In the sequel we refer to elements of σ(U
r
) as {σ
m
: m ∈ U
r
}.
The functions p
r,m
, which are all independent of ω, are constructed
explicitly in a recursive manner. We will demonstrate that the sets U
r
are
composed of n-tuples of nonnegative integers.
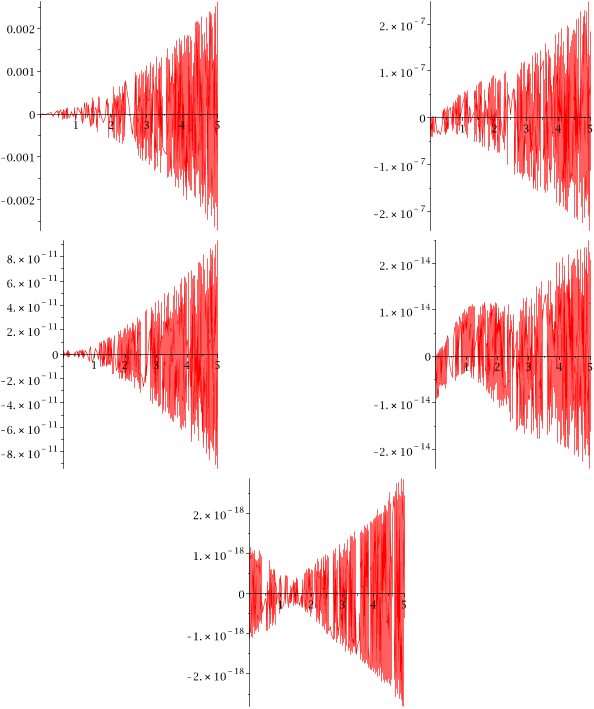
In Section 4 we accompany our narrative by a number of computational
results. Setting the error functions are represented as
s
(t, ω) = y(t) − p
0,0
(t) −
s
X
r=1
1
ω
r
X
m∈U
r
p
r,m
(t)e
iσ
m
ωt
,
we plot the error functions in the figures to illustrate the theoretical analysis.
The expansion solvers are convergent asymptotically. That is, for every
ε > 0, fixed s, the bounded interval for t, there exists ω
0
> 0 such that for
ω > ω
0
, the error function |
s
(t, ω)| < ε. However, for increasing s, fixed t
and ω, we will come to the convergence of the expansion in future paper.
4

2 The linear case
Our concern in this section is with the linear highly oscillatory ODE
(1.6), which we recall for convenience,
y
0
= Ay +
X
m∈U
0
a
m
(t)e
iκ
m
ωt
, t ≥ 0, y(0) = y
0
∈ C
d
, (2.1)
Its closed-form solution can be derived at once from standard variation of
constants,
y(t) = e
tA
y
0
+ e
tA
X
m∈U
0
Z
t
0
e
−xA
a
m
(x)e
iκ
m
ωx
dx. (2.2)
However, the finer structure of the solution is not apparent from (2.2) with-
out some extra work. Each of the integrals hides an entire hierarchy of
scales, and this becomes apparent once we expand them asymptotically.
The asymptotic expansion of integrals with simple exponential operators
is well known: given g ∈ C
∞
[0, t) and |η| 1,
Z
t
0
g(x)e
iηx
dx ∼ −
∞
X
r=1
1
(−iη)
r
h
g
(r−1)
(t)e
iηt
− g
(r−1)
(0)
i
(Iserles, Nørsett and Olver 2006). For any m ∈ U
0
we thus take g(x) =
e
−xA
a
m
(x) and η = κ
m
ω (recall that κ
m
6= 0), therefore
y(t) ∼ e
tA
y
0
−
X
m∈U
0
∞
X
r=1
1
(−iκ
m
ω)
r
"
e
iκ
m
ωt
r−1
X
`=0
(−1)
r−1−`
r − 1
`
A
r−1−`
a
(`)
m
(t)
−e
tA
r−1
X
`=0
(−1)
r−1−`
r − 1
`
A
r−1−`
a
(`)
m
(0)
#
= e
tA
y
0
+
∞
X
r=1
1
ω
r
X
m∈U
0
"
e
iκ
m
ωt
(iκ
m
)
r
r−1
X
`=0
(−1)
`
r − 1
`
A
r−1−`
a
(`)
m
(t)
−
1
(iκ
m
)
r
e
tA
r−1
X
`=0
(−1)
`
r − 1
`
A
r−1−`
a
(`)
m
(0)
#
.
We deduce the expansion (1.7), with U
m
= {0}∪U
0
= {0, 1, ··· , M}, m ∈ N,
and the coefficients
p
0,0
(t) = e
tA
y
0
,
5