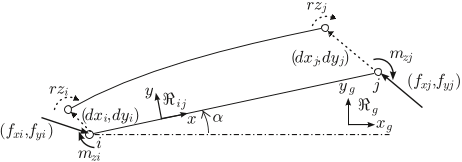
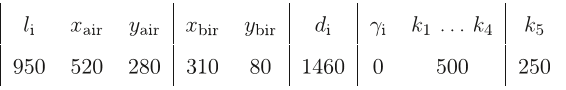scispace - formally typeset
Open AccessJournal ArticleDOI

Elasto-geometrical modeling and calibration of redundantly actuated PKMs

Gaël Ecorchard, +2 more
- 01 May 2010 - 
- Vol. 45, Iss: 5, pp 795-810
TLDR
In this article, an elasto-geometrical and calibration method is proposed to identify the geometrical errors of a planar kinematic mechanism without taking into account the effects of the elastic deformations.
About: 
This article is published in Mechanism and Machine Theory.The article was published on 2010-05-01 and is currently open access. It has received 29 citations till now. The article focuses on the topics: Kinematics.

read more

Figures
Citations
More filters
Journal ArticleDOI

CAD-based approach for identification of elasto-static parameters of robotic manipulators

Alexandr Klimchik, +2 more
- 01 Nov 2013 - 
TL;DR: An approach for the identification of elasto-static parameters of a robotic manipulator using the virtual experiments in a CAD environment based on the numerical processing of data extracted from the finite element analysis results.
Journal ArticleDOI

Off-line compensation of the tool path deviations on robotic machining: Application to incremental sheet forming

Jérémy Belchior, +5 more
- 01 Aug 2013 - 
TL;DR: In this article, a robust and systematic method is first proposed to derive the elastic model of their structure and an efficient FE simulation of the process is then used to predict accurately the forming forces.
Journal ArticleDOI

A Review of Redundant Parallel Kinematic Mechanisms

Mario Luces, +2 more
- 01 May 2017 - 
TL;DR: Primary advantages of PKM redundancy include workspace enlargement, singularity elimination/ avoidance, and improved joint-torque distribution, in contrast to the main challenges redundant mechanisms present, such as in motion planning and control, and calibration.
Posted Content

CAD-based approach for identification of elasto-static parameters of robotic manipulators

Alexandr Klimchik, +2 more
- 26 Nov 2013 - 
TL;DR: In this paper, an approach for the identification of elasto-static parameters of a robotic manipulator using the virtual experiments in a CAD environment is presented, based on the numerical processing of the data extracted from the finite element analysis results, which are obtained for isolated manipulator links.
Journal ArticleDOI

Redundancy in Parallel Mechanisms: A Review

Clément Gosselin, +1 more
- 01 Jan 2018 - 
References
More filters
Book

Solving least squares problems

Charles L. Lawson, +1 more
TL;DR: Since the lm function provides a lot of features it is rather complicated so it is going to instead use the function lsfit as a model, which computes only the coefficient estimates and the residuals.
Journal ArticleDOI

Solving Least Squares Problems

Ake Bjork, +2 more
- 01 Jul 1976 - 
Journal ArticleDOI

Solving Least Squares Problems.

Robert F. Ling, +2 more
- 01 Dec 1977 - 
Journal ArticleDOI

Dynamics and control of redundantly actuated parallel manipulators

Hui Cheng, +2 more
- 01 Dec 2003 - 
TL;DR: In this article, a simple scheme for computing the inverse dynamics of a redundant actuation of a parallel manipulator is proposed, and four basic control algorithms, a joint-space proportional derivative (PD), a PD control in generalized coordinates, an augmented PD control, and a computed-torque control, are formulated.
Journal ArticleDOI

Stiffness analysis of overconstrained parallel manipulators

A. Pashkevich, +3 more
- 01 May 2009 - 
TL;DR: A new stiffness modeling method for overconstrained parallel manipulators with flexible links and compliant actuating joints is presented, based on a multidimensional lumped-parameter model that replaces the link flexibility by localized 6-dof virtual springs that describe both translational/rotational compliance and the coupling between them.
Related Papers (5)

Design and analysis of a redundantly actuated parallel mechanism for rapid machining

JongWon Kim, +6 more

A systematic analytical method for PKM stiffness matrix calculation

D. Deblaise, +2 more

Internal Preload Control of Redundantly Actuated Parallel Manipulators—Its Application to Backlash Avoiding Control

Andreas Müller
- 01 Aug 2005 - 

Force redundancy in parallel manipulators: Theoretical and practical issues

Bhaskar DasGupta, +1 more
- 01 Aug 1998 - 

Parametric stiffness analysis of the Orthoglide

Félix Majou, +4 more
- 01 Mar 2007 - 
Frequently Asked Questions (1)
Q1. What are the contributions mentioned in the paper "Elasto-geometrical modeling and calibration of redundantly actuated pkms" ?

The main originality of this work is to propose an efficient elasto-geometrical and calibration method that allows the identification of both the geometrical and stiffness parameters of redundantly actuated parallel mechanisms with slender links. The first part of the paper explains the proposed method through its application on a simple redundant planar mechanism.