WANG,H.,MURZYN,F.,andCHANSON,H.(2014)."TotalPressureFluctuationsandTwo‐PhaseFlowTurbulenceinHydraulicJumps."
ExperimentsinFluids,Vol.55,No.11,Paper1847,16pages(DOI:10.1007/s00348‐014‐1847‐9)(ISSN0723‐4864).
1
Total pressure fluctuations and two-phase flow turbulence in hydraulic
jumps
Hang Wang (
1
) (*), Frédéric Murzyn (
2
) and Hubert Chanson (
1
)
(
1
) The University of Queensland, School of Civil Engineering, Brisbane QLD 4072, Australia
(
2
) ESTACA Campus Ouest, Parc Universitaire de Laval Changé, BP 53061 Laval Cedex 9, France
(*) Corresponding author: hang.wang@uqconnect.edu.au
Abstract
The large-scale turbulence and high air content in a hydraulic jump restrict the application of many
traditional flow measurement techniques. This paper presents a physical modelling of hydraulic jump,
where the total pressure and air-water flow properties were measured simultaneously with intrusive
probes in the jump roller, namely a miniature pressure transducer and a dual-tip phase detection
probe. The total pressure data were compared to theoretical values calculated based upon void
fraction, water depth and flow velocity measured by the phase-detection probe. The successful
comparison showed valid pressure measurement results in the turbulent shear region with constant
flow direction. The roller region was characterised by hydrostatic pressure distributions, taking into
account the void fraction distributions. The total pressure fluctuations were related to both velocity
fluctuations in the air-water flow and free-surface dynamic above the roller, though the time scales of
these motions deferred substantially.
Keywords
Hydraulic jump, Total pressure, Two-phase flow, Turbulence, Physical modelling
List of symbols
C Time-averaged void fraction
C
max
Local maximum time-averaged void fraction in the shear flow region
D
#
Dimensionless diffusivity in the turbulent shear region
D* Dimensionless diffusivity in the free-surface region
d
1
Inflow water depth immediately upstream of the jump toe [m]
F Bubble count rate [Hz]
F
clu
Longitudinal bubble cluster count rate [Hz]
(F
clu
)
max
Maximum cluster count rate in the shear flow region [Hz]
F
fs
Characteristic free-surface fluctuation frequency [Hz]
F
max
Maximum bubble count rate in the shear flow region [Hz]
F
p
(H)
Upper total pressure fluctuation frequency [Hz]
F
p
(L)
Lower total pressure fluctuation frequency [Hz]
Fr
1
Inflow Froude number,
11 1
Fr = V g×d
g Gravity acceleration [m/s
2
]
h Upstream gate opening [m]
L
r
Length of jump roller [m]
P Time-averaged total pressure [Pa]
P
k
Kinetic pressure [Pa]
P
max
Maximum mean total pressure in the shear flow region [Pa]
P
o
Piezometric pressure [Pa]
p' Standard deviation of total pressure [Pa]
p'
max
Maximum total pressure fluctuation [Pa]
Q Flow rate [m
3
/s]

WANG,H.,MURZYN,F.,andCHANSON,H.(2014)."TotalPressureFluctuationsandTwo‐PhaseFlowTurbulenceinHydraulicJumps."
ExperimentsinFluids,Vol.55,No.11,Paper1847,16pages(DOI:10.1007/s00348‐014‐1847‐9)(ISSN0723‐4864).
2
Re
Reynolds number,
11
Re =ρ×V ×d μ
T Time lag for maximum cross-correlation coefficient [s]
T
0.5
Time lag for maximum auto-correlation coefficient [s]
Tu Turbulence intensity
Tu" Decomposed turbulence intensity of high-frequency signal component
U Free-stream velocity in upstream supercritical flow [m/s]
V Average air-water interfacial velocity [m/s]
V
max
Maximum interfacial velocity in the shear flow region [m/s]
V
recirc
Average recirculation velocity in the free-surface region [m/s]
V
1
Average inflow velocity [m/s]
v' Standard deviation of interfacial velocity [m/s]
W Channel width [m]
x Longitudinal distance from the upstream gate [m]
x
1
Longitudinal position of jump toe [m]
Y
Cmax
Characteristic elevation of local maximum void fraction in the shear region [m]
Y
Fmax
Characteristic elevation of maximum bubble count rate in the shear region [m]
Y
Pmax
Characteristic elevation of maximum mean total pressure in the shear region [m]
Y
p'max
Characteristic elevation of maximum total pressure fluctuation in the shear region
[m]
Y
Vmax
Characteristic elevation of maximum interfacial velocity in the shear region [m]
Y
0.5
Characteristic elevation of half maximum interfacial velocity [m]
Y
50
Characteristic elevation where C = 0.5 [m]
Y
90
Characteristic elevation where C = 0.9 [m]
y Vertical distance from the channel bed [m]
y* Characteristic elevation of local minimum void fraction [m]
z Transverse distance from the channel centreline [m]
Δx Longitudinal separation distance between two phase-detection probe sensors [m]
δ Inflow boundary layer thickness at channel bed [m]
μ Water dynamic viscosity [Pa×s]
ρ
Water density [kg/m
3
]
τ Time lag [s]
τ
0.5
Time lag between maximum and half maximum cross-correlation coefficient [s]
1 Introduction
A hydraulic jump is a rapidly-varied open channel flow characterised by a sudden transition from a
supercritical flow motion to a subcritical regime. The jump toe, where the upstream flow impinges
into the downstream region, is a singular locus with discontinuity in velocity and pressure fields
(Rajaratnam 1967). The transition region immediately downstream of the toe is named the jump
roller because of the presence of large-scale vortices and flow recirculation. The jump roller is a
turbulent two-phase flow region with coexistence of and interaction between air entrainment,
turbulence and flow instabilities.
The turbulent nature of hydraulic jump leads to an efficient energy dissipation rate. For example, an
inflow Froude number Fr
1
= 9 gives a theoretical energy dissipation rate exceeding 70%, where the
Froude number is defined as Fr
1
= V
1
×(g×d
1
)
-1/2
, V
1
being the average inflow velocity and d
1
the
inflow depth. Therefore hydraulic jumps are often generated in hydraulic structures for the purpose

WANG,H.,MURZYN,F.,andCHANSON,H.(2014)."TotalPressureFluctuationsandTwo‐PhaseFlowTurbulenceinHydraulicJumps."
ExperimentsinFluids,Vol.55,No.11,Paper1847,16pages(DOI:10.1007/s00348‐014‐1847‐9)(ISSN0723‐4864).
3
of energy dissipation (Fig 1). However, the large shear force and fluctuating motions of the flow may
challenge the strength of construction, e.g., on the bottom of the jump in a stilling basin. In the early
20
th
century, the attention to hydraulic jump was first triggered with the design of energy dissipators,
which was developed by USBR (U.S. Bureau of Reclamation) in 1940s and 1950s (Riegel and Beebe
1917, Peterka 1958). A number of studies contributed to the pressure quantification mainly beneath
hydraulic jumps (Vasiliev & Bukreyev 1967, Schiebe 1971, Abdul Khader & Elango 1974, Lopardo
& Henning 1985, Fiorotto & Rinaldo 1992, Yan & Zhou 2006, Lopardo & Romagnoli 2009). The
relationship between cavitation occurrence and pressure fluctuations was investigated (Narayanan
1980). The pressure fluctuations were further correlated with water level fluctuations and/or velocity
turbulence in some limited flow conditions with minor aeration (Onitsuka et al. 2009, Lopardo 2013).
In most prototype conditions with large inflow Froude number, the air entrainment in hydraulic jump
is significant. Air entrapped at the jump toe as well as through the rough roller surface is advected
downstream by large vortical structures (Long et al. 1991). The diffusive advection of air bubbles
interplays with the turbulence development. The studies of two-phase flow properties were
represented by Rajaratnam (1962), Resch & Leutheusser (1972) and Chanson (1995) describing the
air concentration and interfacial velocity characteristics using air-water interface detection
techniques. The turbulence characterisation was promoted by Chanson & Toombes (2002) and
Chanson & Carosi (2007) and recently developed by Wang et al. (2014) based upon statistical
analysis of interface detection signals. In a few attempts of numerical modelling, the air entrainment
was rarely taken into account together with the dynamic features of the flow (Richard & Gavrilyuk
2013). Physical modelling with consideration of simultaneous air entrainment and flow
turbulence/fluctuations included Cox & Shin (2003), Murzyn & Chanson (2009) and Wang &
Chanson (2014).
Direct pressure measurement in hydraulic jump flows with strong air entrainment are lacking despite
the significance in hydraulic engineering. This paper presents new experiments measuring the total
pressure distributions within the jump roller. The air-water flow properties were characterised at the
adjacent locations, and the water level fluctuations above were recorded as well. The application of
total pressure transducer in such turbulent bubbly flow was justified by a comparison between the
total pressure output and calculations based upon air-water flow measurement results. The present
work provides new information on the flow regime and fluctuating nature of hydraulic jumps, and
allows further investigation on the interactions between turbulence, aeration and flow instabilities in
such a flow.
2 Physical modelling and instrumentation
2.1 Dimensional considerations
Any theoretical and numerical analyses of hydraulic jumps are based upon a large number of
relevant equations to describe the two-phase turbulent flow motion and the interaction between
entrained air and turbulence. The outputs must be tested against a broad range of gas-liquid flow
measurements:"Unequivocally [...] no experimental data means no validation" (Roache 2009).
Physical modelling requires the selection of a suitable dynamic similarity (Liggett 1994).
Considering a hydraulic jump in a smooth horizontal rectangular channel, dimensional
considerations give a series of dimensionless relationships in terms of the turbulent two-phase flow
properties at a position (x,y,z) within the hydraulic jump roller as functions of the inflow properties,
fluid properties and channel configurations. Using the upstream flow depth d
1
as the characteristic
length scale, a dimensional analysis yields

WANG,H.,MURZYN,F.,andCHANSON,H.(2014)."TotalPressureFluctuationsandTwo‐PhaseFlowTurbulenceinHydraulicJumps."
ExperimentsinFluids,Vol.55,No.11,Paper1847,16pages(DOI:10.1007/s00348‐014‐1847‐9)(ISSN0723‐4864).
4
11 11
1
22
11111 111111
F×d x-x v ' x
Pp'Vv' yz W
, , , ,C, ,... = F , , ,Fr ,Re, , , ,...
0.5×ρ×V 0.5×ρ×V V V V d d d V d d
(1)
where P and V are the total pressure and velocity respectively, p' and v' are pressure and velocity
fluctuations, C is the void fraction, F is the bubble count rate, x
1
is the jump toe position, Re is the
Reynolds number, W is the channel width and the subscript 1 refers to the inflow conditions. In a
hydraulic jump, the momentum considerations demonstrated the significance of the inflow Froude
number, and the selection of the Froude similitude derives implicitly from basic theoretical
considerations (Lighthill 1978, Liggett 1994). Equation (1) shows that measurements in small size
models might be affected by viscous scale effects because the Reynolds number is grossly
underestimated. In the present study, the experiments were performed in a relatively large-size
facility to minimise scale effects (Murzyn & Chanson 2008, Chanson & Chachereau 2013).
2.2 Experimental setup and flow conditions
The experimental channel was 3.2 m long and 0.5 m wide, built with horizontal HDPE bed and 0.4 m
high glass sidewalls (Fig 1b). The inflow was supplied to the flume from a constant head tank. A
rounded undershoot gate of the head tank induced a horizontal impinging flow without contraction.
The gate opening was set at h = 0.02 m, and hydraulic jumps were generated at x
1
= 0.83 m
downstream of the gate. The inflow depth was measured using a point gauge right upstream of the
jump toe. The tailwater depth and jump toe position were controlled by an overshoot gate at the end
of the channel. The flow rate was measured with a Venturi meter in the supply line. While the flow
rate measurement was within an accuracy of 2%, the precision of the determination of inflow depth
and jump toe position relied largely on the fluctuation level of the flow.
Four inflow Froude numbers Fr
1
= 3.8, 5.1, 7.5 and 8.5 were tested, corresponding to Reynolds
numbers 3.5×10
4
< Re < 8.0×10
4
. The total pressure and two-phase flow properties were measured
locally with intrusive total pressure probe and phase-detection probe. The probes were placed side by
side with a 9 mm transverse distance between the sensor tips and sampled at a number of elevations
in a vertical cross-section on the channel centreline. The instantaneous water elevation above the
measurement location was measured non-intrusively with an acoustic displacement meter. The
instrumental setup is illustrated in Figure 2, and the flow conditions are summarised in Table 1 along
with the longitudinal positions of the scanned cross-sections. With an inflow length x
1
/h = 41.5, the
inflow conditions were characterised by partially-developed boundary layer at the channel bed (δ/d
1
< 1 at x = x
1
, Table 1, 7
th
column). Figure 3a presents typical inflow velocity profiles measured with
a Prandtl-Pitot tube along the channel centreline. A developing boundary layer was shown with a
constant free-stream velocity U. Figure 3b compares the free-stream velocity U with the average
inflow velocity V
1
for a broader range of flow conditions. The results indicated U ≈ 1.1×V
1
because
the velocities in boundary layers were lower than the cross-sectional average. Resch & Leutheusser
(1972) and Thandaveswara (1974) compared the air-water flow properties for different types of
inflow conditions (partially-developed, fully-developed and per-entrained). The presence of highly-
aerated shear flow region (see 3.2.1 below) was only observed for partially-developed inflow
conditions, with the shortest aeration length (Chanson 1997).
2.3 Instrumentation
The total pressure probe consisted of a silicon diaphragm sensor mounted on the probe tip. The
sensor was a miniature Micro-Electro-Mechanical-System technology based pressure transducer
(Model MRV21, by MeasureX, Australia). Such a diaphragm pressure sensor is not affected by the

WANG,H.,MURZYN,F.,andCHANSON,H.(2014)."TotalPressureFluctuationsandTwo‐PhaseFlowTurbulenceinHydraulicJumps."
ExperimentsinFluids,Vol.55,No.11,Paper1847,16pages(DOI:10.1007/s00348‐014‐1847‐9)(ISSN0723‐4864).
5
presence of bubbles and does not require to be purged. The sensor had a 5 mm outer diameter with 4
mm diameter sensor. The model provided a measurement range between 0 and 1.5 bars (absolute
pressures). The response frequency was in excess of 100 kHz. The sampling frequency was set at 5
kHz in the present study, though the signal was filtered by a signal amplification system to eliminate
noises above 2 kHz. A daily calibration was conducted and regularly checked, because the output
voltage appeared to be temperature and ambient-pressure sensitive. The largest uncertainty of the
total pressure measurements was thought to be introduced by the fluctuations in atmospheric
pressure reading.
The dual-tip phase-detection probe was designed to pierce bubbles and droplets with its two needle
sensors and worked based upon the difference in electrical resistance between air and water. The
needle sensor tips (0.25 mm inner diameter) were separated longitudinally by Δx = 7.25 mm. While
the signal of each sensor gave the local void fraction and bubble count rate data, a cross-correlation
between the signals provided an average time T of the air-water interfaces travelling over the
distance Δx, yielding a mean longitudinal interfacial velocity V = Δx/T. The phase-detection probe
was excited by an electronic system designed with a response time less than 10 µs, and scanned at 5
kHz simultaneously with the total pressure probe and an acoustic displacement meter above the
probe leading tip. A Microsonic
TM
Mic+25/IU/TC acoustic displacement meter measured the
instantaneous water elevation with a 50 Hz response frequency which was lower than the sampling
rate. The sensor height was carefully adjusted to ensure that the displacement meter measurement
range covered the maximum free-surface fluctuations, and the erroneous samples caused by
splashing droplets were removed from the signal.
The simultaneous sampling of all instruments was performed for 180 s at each measurement location.
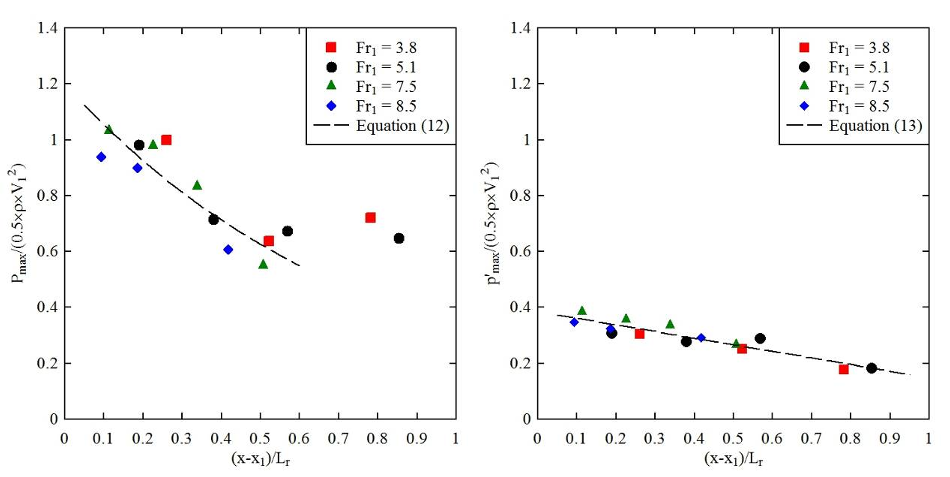
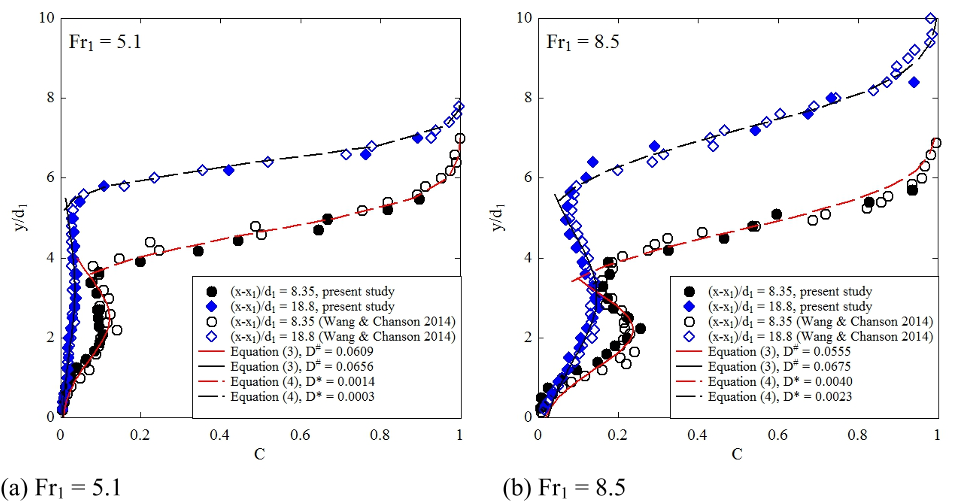
3 Results
3.1 Basic flow patterns
Observations showed some enhanced flow aeration and turbulent fluctuations with increasing Froude
number. The large-scale turbulent structures inside the roller were visualised by the entrained air
bubbles (Fig 1b). The formation of large turbulent structures was linked to the oscillations of jump
toe position and free-surface fluctuations (Long et al. 1991, Wang & Chanson 2014, Wang et al.
2014). These motions were observed in a pseudo-periodic manner, together with the associated air
entrapment and macroscopic variation in velocity and pressure fields. For instance, the slow pressure
pulsations could be felt by placing a hand in the roller. Basically the pulse of increasing impinging
pressure appeared to correspond to the downstream ejection of large vortices.
The water elevation measured along the channel centreline outlined the time-averaged free-surface
profiles similar to the visual observations. The length of hydraulic jump roller L
r
is defined as the
longitudinal distance over which the water elevation increases monotonically. The roller length was
derived from the free-surface profile and found to be an increasing function of the Froude number. A
linear relationship was given by the dataset consisting of Murzyn et al. (2007), Kucukali & Chanson
(2008), Murzyn & Chanson (2009), Wang & Chanson (2014) and the present study:
r
1
1
L
= 6×(Fr -1)
d
for 2 < Fr
1
< 10 (2)