A unified approach to the Clenshaw summation
and the recursive computation of very high
degree and order fully normalised associated
Legendre functions
S. A. Holmes
1
, W. E. Featherstone
2
1
Department of Spatial Sciences, Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia.
e-mail: holmes@vesta.curtin.edu.au, Tel: +61 8 9487 3838 Fax: +61 8 9266 2703
2
Department of Spatial Sciences, Curtin University of Technology, GPO Box U1987, Perth, WA 6845, Australia.
e-mail: W.Featherstone@cc.curtin.edu.au, Tel: +61 8 9266 2734 or 0401 103 734 Fax: +61 8 9266 2703
Send offprint requests to: S. A. Holmes

2
Abstract. Spherical harmonic expansions form partial sums of fully normalised asso-
ciated Legendre functions (ALFs). However, when evaluated increasingly close to the
poles, the ultra-high degree and order (eg. 2700) ALFs range over thousands of orders
of magnitude. This causes existing recursion techniques for computing values of indi-
vidual ALFs and their derivatives to fail. A common solution in geodesy is to evaluate
these expansions using Clenshaw’s (1955) method, which does not compute individual
ALFs or their derivatives. Straightforward numerical principles govern the stability of
this technique. This paper employs elementary algebra to illustrate how these principles
are implemented in Clenshaw’s method. It also demonstrates how existing recursion al-
gorithms for computing ALFs and their first derivatives are easily modified to incorporate
these same numerical principles. These modified recursions yield scaled ALFs and first
derivatives, which can then be combined using Horner’s scheme to compute partial sums,
complete to degree and order 2700, for all latitudes (except at the poles for first deriva-
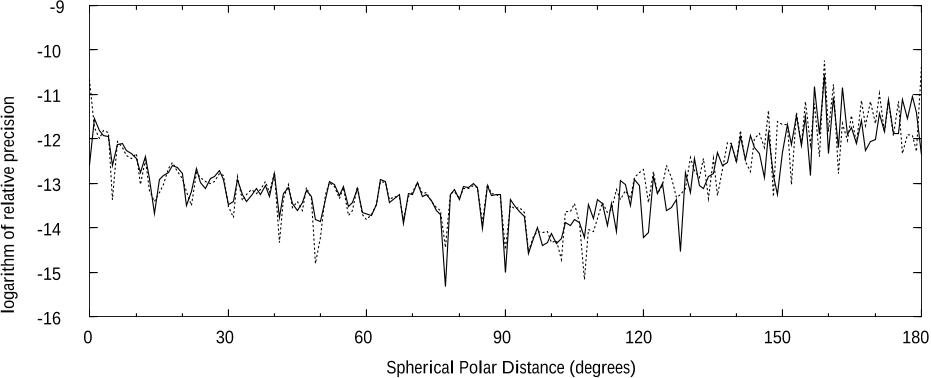
tives). This exceeds any previously published result. Numerical tests suggest that this new
approach is at least as precise and efficient as Clenshaw’s method. However, the principal
strength of the new techniques lies in their simplicity of formulation and implementation,
since this quality should simplify the task of extending the approach to other uses, such
as spherical harmonic analysis.
Key words. Spherical harmonic expansions, Fully normalised associated Legendre Func-
tions, Clenshaw summation, Recursion, Horner’s scheme

3
1 Introduction
Current geodetic practice is witnessing an increase in the construction and use of ultra-
high degree spherical harmonic expansions of the geopotential or topography. For ex-
ample, Wenzel (1998) released coefficients up to degree
1800
, which were empirically
derived to describe the gravitational potential of the Earth. Wenzel (1998) states that the
maximum degree of
1800
for the spherical harmonic model was set by the numerical
stability of the recursion algorithm adopted to compute the required fully normalised as-
sociated Legendre functions (ALFs).
The recent interest in synthetic Earth gravity models, used for comparing and validat-
ing gravity field determination techniques, has already seen the use of ultra-high degree
spherical harmonic expansions. These have taken the form of simple effects models (eg.
Featherstone, 1999; Nov´ak et al., 2001) for which synthetic geopotential coefficients up to
degree and order
2700
and
2160
, respectively, were produced without reference to a mass
distribution. There is also interest in source models in which synthetic geopotential coef-
ficients are generated by analytical or numerical Newtonian integration over a synthetic
global density distribution and topography (eg. Pail, 1999). Hybrids of source and effects
models also exist. For example, Haagmans (2000) combines empirically determined co-
efficients with synthetic ones derived from numerical integration over isostatically com-
pensated source masses to degree and order
2160
. Lastly, other scientific disciplines, such
as meteorology, quantum physics and electronic engineering, are also also showing in-
creased interest in high degree spherical harmonic modelling and analysis.
The numerical means for including the necessary ALFs constitutes the principal chal-
lenge to evaluating ultra-high degree spherical harmonic expansions.Therefore, it is timely

4
to critically examine the accuracy and numerical efficiency of algorithms that compute in-
dividual ALFs and their partial sums.
1.1 Spherical Harmonic Expansions
Truncated spherical harmonic expansions of a function, or its derivatives, reduce to sums
S
(
d
)
of ALFs or their
d
-th derivatives, respectively. These are
S
(
d
)
=
c
M
X
m
=0
(
d
)
m
(1)
where
(
d
)
m
=
2
X
=1
8
>
>
<
>
>
:
X
(
d
)
m
cos
m
for
=1
X
(
d
)
m
sin
m
for
=2
(2)
and
X
(
d
)
m
=
M
X
n
=
E
nm
P
(
d
)
nm
(
)
(3)
For arguments of spherical polar coordinates (
r
,
,
) and for integer degree
n
0
and
order
0
m
n
:
M
is the maximum finite degree of the spherical harmonic expansion;
is an integer that may vary with
m
;
c
is a real numbered constant;
E
nm
is a real num-
ber incorporating the fully normalised spherical harmonic coefficients,
C
nm
1
and
C
nm
2
;
P
nm
(
)
are the fully normalised ALFs; the superscript
(
d
)
indicates the
d
-th derivative
with respect to
, or definite integration (
d
=
1
) between two parallels. This paper deals
only with undifferentiated functions (
d
=0
) or first derivatives of these functions (
d
=1
).
For
d
= 0
, the superscript
(
d
)
is omitted. Thus
S
(0)
,
(0)
m
,
X
(0)
m
and
P
(0)
nm
(
)
are written
S
,
m
,
X
m
and
P
nm
, respectively. First derivatives of these quantities are written
S
(1)
,
(1)
m
,
X
(1)
m
and
P
(1)
nm
(
)
, respectively. The general notation
S
(
d
)
,
(
d
)
m
,
X
(
d
)
m
and
P
(
d
)
nm
(
)
is used whenever a textual or mathematical reference applies to both the undifferentiated
quantities and the first derivatives simultaneously.

5
The example of a truncated spherical harmonic expansion of the gravitational potential
V
(
r;;
)
is instructive here. Often, it is written as
V
(
r;;
)=
GM
r
+
GM
r
M
X
n
=2
a
r
n
n
X
m
=0
(
C
nm
1
cos
m
+
C
nm
2
sin
m
)
P
nm
(
)
(4)
where
GM
is the product of the Universal gravitational constant and the mass of the
Earth. Alternatively, Eq. (4) may be written as
V
(
r;;
) =
GM
r
+
GM
r
M
X
m
=0
"
cos
m
M
X
n
=
a
r
n
C
nm
1
P
nm
(
)
+sin
m
M
X
n
=
a
r
n
C
nm
2
P
nm
(
)
#
(5)
where
is either
2
or
m
; whichever is the greater. Relating Eq. (5) to the form of Eqs. (1)
to (3) yields
E
nm
=
8
>
>
<
>
>
:
a
r
n
C
nm
1
;
for
=1
a
r
n
C
nm
2
;
for
=2
(6)
and
X
m
=
M
X
n
=
a
r
n
C
nm
P
nm
(
)
(7)
When evaluating gravimetric quantities (eg., disturbing potential, geoid heights, grav-
ity anomalies, etc.) in a sequence of points for which
r
and
are constant (ie., along a
geodetic parallel), the form of Eq. (5) is numerically more efficient than that of Eq. (4) (cf.
Tscherning et al., 1983). This is because each
X
m
in Eq. (3) is independent of
, and thus
need only be evaluated once for each parallel. If all such computation points are equally
spaced in longitude, further numerical efficiencies can be achieved through application
of the recursion algorithm developed by Rizos (1979). Abd-Elmotaal (1997) contains a
re-derivation of this algorithm which demonstrates that, contrary to the approach of Ri-
zos (1979), the algorithm can be applied in full without prior rotation of the geopotential
coefficients.