Karlsruher Institut f
¨
ur Technologie
Institut f
¨
ur Baustatik
A Finite element formulation for
piezoelectric shell structures considering
geometrical and material nonlinearities
K. Schulz, S. Klinkel, W. Wagner
Mitteilung 3(2010)
BAUSTATIK

Karlsruher Institut f
¨
ur Technologie
Institut f
¨
ur Baustatik
A Finite element formulation for
piezoelectric shell structures considering
geometrical and material nonlinearities
K. Schulz, S. Klinkel, W. Wagner
Mitteilung 3(2010)
BAUSTATIK
c
Prof. Dr.–Ing. W. Wagner Telefon: (0721) 608–2280
Institut f
¨
ur Baustatik Telefax: (0721) 608–6015
Karlsruher Institut f
¨
ur Technologie E–mail: info@ibs.kit.edu
Kaiserstr. 12 Internet: http://www.ibs.kit.edu
76131 Karlsruhe

A Finite element formulation for piezoelectric shell structures
considering geometrical and material nonlinearities
K. Schulz
[1]
,S.Klinkel
[2]
and W. Wagner
[1]
[1 ]Karlsruhe Institute of Technology(KIT), Institute for Structural Analysis, Kaiserstr.12, 76131 Karl-
sruhe, Germany
[2 ]Statik u. Dynamik d. Tragwerke, Technische Universit¨at Kaiserslautern, Paul-Ehrlich-Str. 14, D-
67663 Kaiserslautern, Germany
Abstract In this paper we present a nonlinear finite element formulation for piezoelectric
shell structures. Based on a mixed multi field variational formulation, an electro-mechanical
coupled shell element is developed considering geometrically and materially nonlinear behavior
of ferroelectric ceramics. The mixed formulation includes the independent fields of displace-
ments, electric potential, strains, electric field, stresses, and dielectric displacements. Besides
the mechanical degrees of freedom, the shell counts only one electrical degree of freedom.
This is the difference of the electric potential in thickness direction of the shell. Incorporating
nonlinear kinematic assumptions, structures with large deformations and stability problems
can be analyzed. According to a Reissner-Mindlin theory, the shell element accounts for con-
stant transversal shear strains. The formulation incorporates a three-dimensional transversal
isotropic material law, thus the kinematic in thickness direction of the shell is considered.
The normal zero stress condition and the normal zero dielectric displacement condition of
shells are enforced by the independent resultant stress and resultant dielectric displacement
fields. Accounting for material nonlinearities, the ferroelectric hysteresis phenomena are con-
sidered using the Preisach model. As a special aspect, the formulation includes temperature-
dependent effects and thus the change of the piezoelectric material parameters due to the
temperature. This enables the element to describe temperature dependent hysteresis curves.
1 Introduction
Piezoelectric material plays an important role for sensor and actuator devices. In the course
of optimization of systems, shell structures have become more and more interesting. In recent
years, several piezoelectric shell formulations based on the finite element method have been
introduced. One can distinguish between solid shell elements, see e.g. References [1, 2, 3],
and classical formulations, which model the shell by a reference surface, see e.g. References
[4, 5, 6, 7, 8, 9, 10, 11]. Some of these element formulations are restricted to shallow shell
structures, [5, 6, 9, 11], where the initial shell curvature is assumed to be small. In order to
consider laminated structures, the above mentioned formulations include a more or less sophis-
ticated laminate theory. References [5, 10, 12, 13, 14] point out that geometrically nonlinear
characteristics can significantly influence the performance of piezoelectric systems, especially
for the sensor usage. A geometrically nonlinear theory that incorporates large rotations is
presented in References [1, 5, 6, 12]. A common assumption in piezoelectric models is that
the electric field is constant through the thickness. This is not correct for bending dominated
problems. According to Reference [15], a quadratic approach for the electric potential through
the thickness is necessary to fulfill the electric charge conservation law. Shell formulations
incorporating a quadratic thickness potential can be found in References [16, 8, 7]. Mixed
1

shell formulations including independent fields for the electric potential, the electric field, the
dielectric displacement as well as the mechanical fields of the displacement, the strain, and
the stress can be found in [19].
Accounting for nonlinear material behavior, the polarization state has to be analyzed. Due
to high electric fields, ferroelectric switching processes take place and the material proper-
ties change. To consider the resultant ferroelectric hysteresis phenomena, one can refer to
microscopic models, see References [20, 21], and macroscopic models, see e.g. References
[22, 23, 24, 25, 26, 27, 28]. Microscopic analysis looks at single crystals and models the
switching process via an energy criterion. A macroscopic approach using a switching criterion
based on thermodynamic energy function is presented in [22, 23, 24, 25, 26, 27]. Macro-
scopic phenomenological hysteresis models can be found in Reference [28]. A well known
phenomenological model is the Preisach model, see Reference [47]. Several piezo-mechanical
coupled formulations have used the Preisach model to display piezoelectric material behavior,
see References [30, 31, 32]. A shell element that accounts for material nonlinearities is [33]; it
is based on a phenomenological switching function. In order to consider the nonlinear material
behavior in a classical shell formulation, the strain and the electric field in thickness direction
have to be comprised. A classical mechanical shell element incorporating three dimensional
constitutive equations is e.g. proposed by Reference [34]. The influence of the temperature on
piezoelectric material behavior has been studied experimentally in References [36, 37, 38, 39].
[39] shows that the ferroelectric hysteresis curves become smaller with increasing temperature.
A micropolar model to consider the temperature-dependent relation between the electric field
and the polarization is introduced by [40]. Here, the influence of mechanical stress is neglected
and there is no remark on the strain behavior. A simple one-dimensional phenomenological
model considering the strain is presented in Reference [41]. The authors assume a volume
part of paraelectric phase for every hysteresis. [35] presents a piezoelectric plate element
considering the deformation of a linear temperature gradient through the thickness, and gives
the results depending on the piezoelectric material parameters for different temperature lev-
els. Thus, temperature can influence the performance of piezoelectric shell structures due to
a change of the temperature dependent material parameters. The essentiell aspects of the
piezoelectric shell formulation presented in this paper are the following:
(i) The bilinear, four-node shell element is based on a six field variational functional. Be-
sides the six mechanical degrees of freedom, three displacements and three rotations, the
only electrical degree of freedom is the difference of the electric potential in thickness
direction;
(ii) The element includes nonlinear kinematic assumptions, thus a geometric nonlinear anal-
ysis becomes feasible;
(iii) The formulation incorporates three dimensional transversal isotropic constitutive equa-
tions. In the shell formulation a linear approach for both the strain and the electric
field in thickness direction is considered;
(iv) Using the Preisach model, the material nonlinear ferroelectric hysteresis effects are in-
corporated. Here the change of the saturation parameters of the polarization and the
strain due to temperature is phenomenologically included, thus temperature-dependent
hysteresis curves can be determined.
2

2 Kinematics
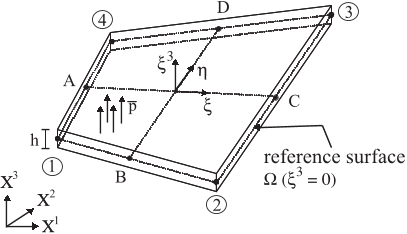
We model the shell by a reference surface Ω with the boundary Γ. Every point of Ω is part
of the Euklidean space B. In order to display the geometry of the structure in B,wedenote
a convected coordinate system of the body ξ
i
andanoriginO with the global cartesian
coordinate system e
i
. The initial thickness of the shell in the reference configuration is given
as h, thus we define the arbitrary reference surface by the thickness coordinate ξ
3
=0with
h
−
≤ ξ
3
≤ h
+
. X(ξ
1
,ξ
2
)andx(ξ
1
,ξ
2
) denote the position vectors of the shell surface Ω by
means of the convective coordinates in the reference and the current configuration respectively.
The covariant tangent vectors for the reference and the current configuration, A
i
and a
i
,are
given as
A
i
=
∂X
∂ξ
i
, a
i
=
∂x
∂ξ
i
,i=1, 2, 3 . (1)
The contravariant basis A
i
is defined by the orthogonality δ
j
i
= A
i
· A
j
. The director vector
D(ξ
1
,ξ
2
)with|D(ξ
1
,ξ
2
)| = 1 is given perpendicular to Ω. It holds D = A
3
. We obtain the
corresponding inextensible director vector d of the current configuration with the rotation
tensor R by the orthogonal transformation d = RD. In the following, we refer to the notation
that Latin indices range from 1 to 3 and Greek indices range from 1 to 2, whereas we use
the summation convention for repeated indices. Commas denote a partial differentiation with
respect to the coordinates ξ
α
. A displacement u can be determined by the difference of the
current and the initial position vectors u = x − X. Including a Reissner-Mindlin kinematic,
we consider transverse shear strain, thus it holds d · x,
α
= 0. For the geometric in-plane and
thickness strains we assume
E
αβ
= ε
αβ
+ ξ
3
κ
αβ
2E
α3
= γ
α
E
33
=0 .
(2)
We write the membrane strains ε
αβ
, the curvatures κ
αβ
, and the shear strains γ
α
of the shell,
see Reference [42], as
ε
αβ
=
1
2
(x,
α
·x,
β
−X,
α
·X,
β
)
κ
αβ
=
1
2
(x,
α
·d,
β
+x,
β
·d,
α
−X,
α
·D,
β
−X,
β
·D,
α
)
γ
α
= x,
α
·d − X,
α
·D .
(3)
The electric field
E =
E
1
E
2
E
3
T
is given as the gradient field of the electric potential
ϕ. Due to the shell geometry, we assume that the piezoelectric material is poled in thickness
direction and the electrodes are arranged at the lower and upper surface. Therefore, we only
consider the difference of the electric potential in thickness direction of the shell Δϕ and write
the geometric electric field
E
g
=
E
1
E
2
0
T
as
E
g
= −
∂Δϕ
∂ξ
i
A
i
. (4)
We summarize the strains and the electric field of the shell in a generalized geometric strain
vector ε
g
(v)
ε
g
(v)=[ε
11
,ε
22
, 2ε
12
,κ
11
,κ
22
, 2κ
12
,γ
1
,γ
2
,
E
1
,
E
2
]
T
. (5)
3