scispace - formally typeset
Search or ask a question
Journal Article•DOI•

A continuous-time model of the term structure of interest rates with fiscal-monetary policy interactions

Massimiliano Marzo1, Silvia Romagnoli1, Paolo Zagaglia1•
University of Bologna1
24 Oct 2008-Social Science Research Network-Vol. 2, Iss: 1, pp 1-28
TL;DR: In this article, the term structure implications of the fiscal theory of price level determination were studied and the intertemporal budget constraint of the government in a general equilibrium model in continuous time was introduced.
Abstract: We study the term structure implications of the fiscal theory of price level determination We introduce the intertemporal budget constraint of the government in a general equilibrium model in continuous time Fiscal policy is set according to a simple rule whereby taxes react proportionally to real debt We show how to solve for the prices of real and nominal zero coupon bonds

Summary (3 min read)

Jump to: [1 Introduction] – [2 The model economy] – [3 Fiscal and monetary policy] – [4 The optimal choice problem] – [5 Definition of equilibrium] – [6 The equilibrium in the continuous time limit] – [7 A specialized economy] – [8 The real spot interest rate] – [9 The term structure of real interest rates] – [10 The term structure of nominal interest rates] – [11 Simulation results] and [12 Concluding remarks]

1 Introduction

  • This considerations holds both for the finance and macroeconomics literature.
  • The authors also study how the term structure responds to the fiscal parameters.
  • The nominal and real term structure for zero coupon bonds is derived in section 9.

2 The model economy

  • The authors study an economy populated by a representative agent that maximizes over the composition of her portfolio along the lines of the traditional literature on consumption and asset pricing.
  • The authors model the economy at discrete time intervals of length ∆t.
  • The representative agent chooses its portfolio holdings by maximizing the following utility function ∞∑ t=0 e−βtE0 { u ( Ct, Mt Pt )} ∆t (1) where β is the discount factor.
  • In equation (1), Ct indicates the level of consumption over the interval [t, t + ∆t], Mt is the nominal money stock providing utility to the representative agent over the interval of length [t−∆, t], and Pt is the price of the consumption good.
  • In equation ( 3), the preference parameter φ must be chosen so that the nominal and real spot rates determined under the assumption of absence of arbitrage opportunities are also equilibrium values .

3 Fiscal and monetary policy

  • The main point of this paper is to examine the impact of the interaction between monetary and fiscal policy on the the term structure of interest rates.
  • The authors define the money supply aggregate (in nominal terms) as M st = Ht + Ft. (5) In equation (5) they observe that the total money supply is determined by two components.
  • Existing literature consists in the key role for the government budget constraint ∆Dt+∆t + ∆Ft+∆t = ∆it+∆tDt −∆Tt+∆t (11) where Moreover, ∆Tt+∆t is the stochastic process for taxes.
  • Following the fiscal theory of price level, the authors assume that the government sets taxes according to the simple rule rule ∆Tt+∆t = φ1Dt∆t +.

4 The optimal choice problem

  • The investor can choose among one real and one nominal bond (both risk free), and N − 2 equities.
  • The return on bond are it for the nominal bond, and rt for the real bond.
  • Mt, for cash, Ct for consumption and xt for equity holdings.
  • AN,t represent the unit of financial asset held from (t−∆t) to t.3.
  • The choice problem of the representative investor consists in the maximization of the utility function (3) subject to the budget constraint (22).

5 Definition of equilibrium

  • The equality between money demand and supply is stated in equation (29), while equation (30) states that each agent’s demand for equity shares must equal the supply.
  • Equations (32) and (35) state that the representative investor must be indifferent between investing an amount of money equal to PCt in a real risk-free bond and holding the same amount in cash.
  • Monetary policy and the asset market are tied together through equations (35) and (34), which establish the consistency between the money supply and asset markets.
  • The equality (36) rules out bubbles in the price level of any risky asset.

6 The equilibrium in the continuous time limit

  • In this section the authors characterize the equilibrium for the continuous time limit.
  • These results are independent from the assumptions made on the role of fiscal and monetary policies in the determination of the equilibrium.
  • For this reason, the results from this section are similar to Baksi and Chen (1996) Balduzzi (1998).
  • In the continuous time limit equilibrium, the commodity price level is given at time t by 1 PCt =.

7 A specialized economy

  • In what follows the authors lay out a specific model used to derive the stochastic processes for the price level and the other variables.
  • Each type of money supply has two components, a drift term and a stochastic part.
  • The set of assumptions presented earlier allows us to compute the equilibrium price level of the commodity and the inflation process.
  • After solving for the integral, the authors get equation (62).

8 The real spot interest rate

  • In this section the authors derive the dynamics of the real spot interest rate implied by exogenous the dynamics of the technology process.
  • Since this requires solving the differential equation ( 55), xt is Markov and satisfies the necessary technical conditions to apply the Representation Theorem of Feyman-Kac.4.
  • The authors can now follow the partial differential equation — PDE — approach to compute the real spot rate.
  • Given that the Kolmogorov PDE is verified for all t and xt, the authors can divide it into two parts.
  • One part is dependent and the other one is independent from xt.

9 The term structure of real interest rates

  • Here the authors show how to compute the price of zero coupon bonds as a function of time, technology and the real spot rate.
  • The authors follow again a PDE approach because both xt and rt are Markov and satisfy the necessary technical conditions to apply the Representation Theorem of Feyman-Kac.
  • The authors can then find the solution only by using numerical methods.
  • The term structure of real interest rates can be derived from the relation between the price of zero coupon bond and the continuous real interest rate B (t, T ) = e−θR(t,T ). (92) ¥.

10 The term structure of nominal interest rates

  • The analytical expression for the nominal zero coupon bond, and for the nominal term structure of interest rates.the authors.
  • From the expressions for (93), (94) and (95), the authors observe that the values of the rates for the nominal term structure are higher than those for the real variables if (61) is higher than one.

11 Simulation results

  • The authors now calibrate the model and run numerical simulations to get a better understanding of the relations involved.
  • The intertemporal substitution coefficient β has been set equal to 0.998.
  • Figure 1 shows that the higher the reaction of the tax rate to real debt, the lower µ∗M , and the lower the position of the nominal curve in the plan.
  • Are aware of the limitation of this choice.
  • This is consistent with the results form the fiscal theory of the price level.

12 Concluding remarks

  • In this paper the authors study a simple intertemporal model for the determination of the nominal and real term structure where the interaction between fiscal and monetary plays a key role.
  • In particular, the authors investigate the relation between the term structure of interest rate and the fiscal theory of price level determination.
  • In so doing, the authors move beyond the standard finance models where monetary and technological factors are the sole determinants of the term structure of interest rates.
  • This is likely to shadow more light on the role of monetary policy expectations when also fiscal policy matters.

Did you find this useful? Give us your feedback

Figures (2)

Content maybe subject to copyright    Report

A continuous-time model of the term structure of
interest rates with fiscal-monetary policy interactions
Massimiliano Marzo, Silvia Romagnoli and Paolo Zagaglia
∗
July 2008
Abstract
We study the term structure implications of the fiscal theory of price level
determination. We introduce the intertemporal budget constraint of the gov-
ernment in a general equilibrium model in continuous time. Fiscal policy is set
according to a simple rule whereby taxes react proportionally to real debt. We
show how to solve for the prices of real and nominal zero coupon bonds.
Keywords: Bond pricing, fiscal policy, mathematical methods.
JEL Classification: D9, G12.
∗
Marzo: Department of Economics, Universit`a di Bologna; massimiliano.marzo@unibo.it. Ro-
magnoli: Department of Mathematics, Universit`a di Bologna; silvia.romagnoli@unibo.it. Za-
gaglia: Research Unit, Bank of Finland, and Department of Economics, Stockholm University;
Paolo.Zagaglia@bof.fi. We are grateful to S. Alliney for many suggestions received on the first draft
of this paper. The views expressed here are those of the authors and should not be attributed to
the Bank of Finland.
1
1 Introduction
The theory of price level determination advocated by Leeper (1991), Sims (1994),
Woodford (1996) and Cochrane (1998) has brought to the attention of macroe-
conomists the role of interactions between fiscal and monetary policy. In a nutshell,
the idea is that the price level is determined by the degree of solvency of the govern-
ment. If the expected primary surplus is not sufficient to comply with the intertem-
poral budget constraint of the government, then part of the public debt should be
inflated away if it is default-free.
Although the fiscal theory of price level determination has generated a substan-
tial debate on the capability of fiscal and monetary policy to affect the price level,
study has considered its potential implications for asset prices. This considera-
tions holds both for the finance and macroeconomics literature. For instance, the
continuous-time model of the term structure of interest proposed by Buraschi (2005)
includes lump-sum taxes, but disregards the implications of the government’s budget
constraint. Dai and Philippon (2005) estimates a no-arbitrage ane term structure
model with fiscal variables on U.S. data. They find significant responses of the term
structure of interest rates to the deficit-GDP ratio. The macroeconomic restric-
tions they impose to identify the structural responses are fairly different from those
implied by the fiscal theory of the price level (see Sala, 2004).
The available finance models the term structure of interest rates consider an
explicit role for only two crucial factors, output growth and monetary policy, which
is typically expressed as a diffusion process for the growth of money supply. In this
paper, we consider a general-equilibrium model with money where the ow budget
constraint of the government plays an active role. This provides a link between
monetary and fiscal policy because lump-sum taxes are adjusted as a function of
real debt. We solve the structural model, and derive the law of motion for the
nominal and real interest rates. We also study how the term structure responds to
the fiscal parameters.
2
This paper is organized as follows. The first two sections introduce the reader
to the framework employed to develop the analysis, together with a brief discus-
sion on the fiscal and monetary policy rules adopted. Section 4 and 5, respectively,
discuss the optimization process form the representative investor’s side and the char-
acterization of the equilibrium. Section 6 outlines the continuous time limit of the
equilibrium relationships in discrete time presented in the previous sections. In sec-
tion 7, we consider a specialized economy with a more realistic set of assumptions
for the model. In section 8 we present the solution for the real spot rate. This is
extended in section 9 for the pricing of the entire real term structure. The nominal
and real term structure for zero coupon bonds is derived in section 9. Since the
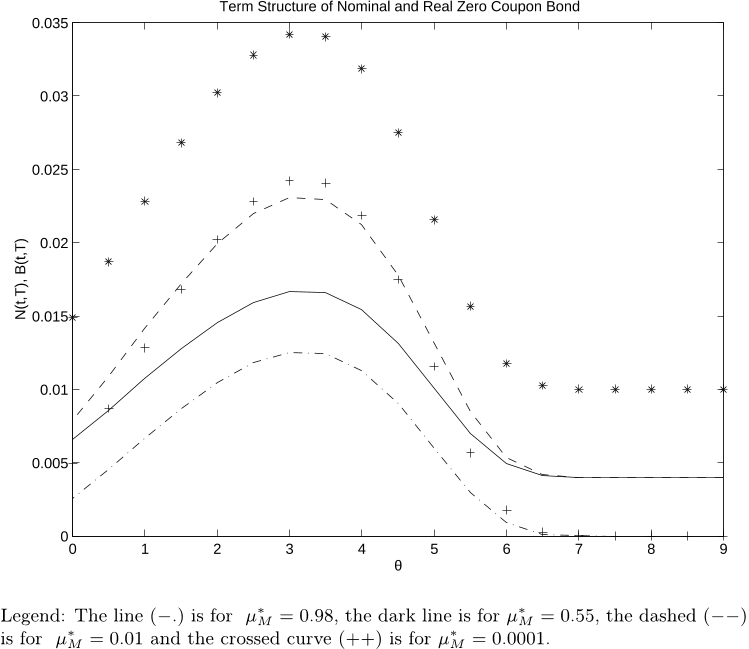
solution does not admit a closed form, we use numerical simulations in section 10
to generate some qualitative results on the shape of the term structure. Section 11
reports some concluding remarks.
2 The model economy
We study an economy populated by a representative agent that maximizes over the
composition of her portfolio along the lines of the traditional literature on consump-
tion and asset pricing. We model the economy at discrete time intervals of length ∆t.
The representative agent chooses its portfolio holdings by maximizing the following
utility function
∞
X
t=0
e
−βt
E
0
½
u
µ
C
t
,
M
t
P
t
¶¾
∆t (1)
where β is the discount factor. In equation (1), C
t
indicates the level of consumption
over the interval [t, t + ∆t], M
t
is the nominal money stock providing utility to the
representative agent over the interval of length [t − ∆, t], and P
t
is the price of the
consumption good. Real money balances M
t
/P
t
enter the utility function of the
household. The utility function is twice continuously differentiable and concave in
3
both consumption and real balances
u
c
> 0, u
m
> 0, u
cc
< 0, u
mm
< 0, u
cm
< 0, u
cc
u
mm
− (u
cm
)
2
> 0 (2)
where the subscript to u indicates the partial derivative. In what follows, we make
the following functional assumption on the utility function
u
µ
C
t
,
M
t
P
t
= φ log C
t
+ (1 − φ) log
µ
M
t
P
t
(3)
This type of utility function is used in Stulz (1986). In equation ( 3), the preference
parameter φ must be chosen so that the nominal and real spot rates determined
under the assumption of absence of arbitrage opportunities are also equilibrium
values (see Corollary 1 in the Appendix).
As a working hypothesis to derive the first order conditions, we consider a model
of pure endowment economy where output growth evolves as
∆Y
t
Y
t
=
Y
t+∆t
− Y
t
Y
t
= µ
Y,t
∆t + σ
Y,t
Ω
Y,t
√
∆t. (4)
The terms µ
Y,t
and σ
Y,t
are, respectively, the conditional expected value and the
standard deviation of output per unit of time and {Ω
Y,t
t = 0, ∆t, . . .} is a standard
normal process.
1
3 Fiscal and monetary policy
The main point of this paper is to examine the impact of the interaction between
monetary and fiscal policy on the the term structure of interest rates. We think
of ‘interactions’ in the sense captured by the “fiscal theory of the price level” of
Leeper (1991), Sims (1994), Woodford (1996), and recently extended by Cochrane
(1998, 1999). This approach states that a tight fiscal policy is a strictly necessary
complement to ensure price stability.
1
A more realistic law of motion for output is introduced in section 7.
4
We define the money supply aggregate (in nominal terms) as
M
s
t
= H
t
+ F
t
. (5)
In equation (5) we observe that the total money supply is determined by two com-
ponents. H
t
is the so called ‘high p owered money’ (or monetary base). F
t
represents
the amount of money needed by the government to budget its balance. Basically,
F
t
is an additional financing source for the government apart from taxes and debt
2
.
We assume that H
t
and F
t
follow the processes described by
∆H
t
H
t
=
H
t+∆t
− H
t
H
t
= µ
H,t
∆t (6)
∆F
t
F
t
=
F
t+∆t
− F
t
F
t
= µ
F,t
∆t + σ
F,t
Ω
F,t
√
∆t (7)
where µ
H,t
and µ
F,t
are, respectively, the mean of the stochastic process of the mon-
etary base and of the financing to public debt. In (6), the stochastic process for
H
t
does not have a standard error term, implying that the monetary base possesses
only a deterministic component. The process leading F
t
, instead, has a standard de-
viation term σ
F,t
, where {Ω
F,t
t = 0, ∆t, . . .} are standard normal random variables.
From (5), (6) and (7), we can write the stochastic process for the total money
supply M
s
∆M
s
t
M
s
t
=
M
s
t+∆t
− M
s
t
M
s
t
= µ
M,t
∆t + σ
M,t
Ω
M,t
√
∆t (8)
µ
M,t
= µ
H,t
+ µ
F,t
(9)
σ
M,t
Ω
M,t
= σ
F,t
Ω
F,t
. (10)
At a first glance, these expressions stress that the central bank is assumed to target
money growth.
The subsequent building block of the model assigns a proper macroeconomic
role to the government. The innovation introduced in this paper with respect to the
2
F
t
can be thought of as the demand for money balances expressed by the government.
5
Citations
More filters
Journal Article•DOI•
Bank Competition and Collateral: Theory and Evidence

[...]

Christa Hainz1, Laurent Weill2, Christophe J. Godlewski2•
Ifo Institute for Economic Research1, EM Strasbourg Business School2
01 Oct 2013-Journal of Financial Services Research
TL;DR: In this article, the authors investigate the impact of bank competition on the use of collateral in loan contracts and show that the presence of collateral is more likely when bank competition is low.
Abstract: We investigate the impact of bank competition on the use of collateral in loan contracts. We analyze asymmetric information about the borrowers’ type in a Salop model in which banks choose between screening the borrower and asking for collateral. We show that the presence of collateral is more likely when bank competition is low. We then test this prediction empirically on a sample of bank loans from 70 countries. We perform logit regressions of the presence of collateral on bank competition, measured by the Lerner index. Our empirical tests corroborate the theoretical predictions that bank competition reduces the presence of collateral. These findings survive several robustness checks.

80 citations

Journal Article•DOI•
Testing the Structural Interpretation of the Price Puzzle with a Cost‐Channel Model

[...]

Efrem Castelnuovo1, Efrem Castelnuovo2•
University of Padua1, University of Melbourne2
25 Nov 2009-Social Science Research Network
TL;DR: In this article, the authors estimate a new-Keynesian DSGE model with the cost channel to assess its ability to replicate the price puzzle, i.e., the inflationary impact of a monetary policy shock typically arising in VAR analysis.
Abstract: We estimate a new-Keynesian DSGE model with the cost channel to assess its ability to replicate the price puzzle ie the inflationary impact of a monetary policy shock typically arising in VAR analysis. In order to correctly identify the monetary policy shock, we distinguish between a standard policy rate shifter and a shock to trend inflation ie the time-varying inflation target set by the Fed. While offering some statistical support to the cost channel, our estimated model clearly implies a negative inflation reaction to a tightening of monetary policy. We offer a discussion of the possible sources of mismatch between the VAR evidence and our own.

47 citations

Journal Article•DOI•
Shattered on the Rock? British Financial Stability from 1866 to 2007

[...]

Alistair Milne1, Geoffrey Wood2•
Loughborough University1, University of London2
19 Dec 2008-Social Science Research Network
TL;DR: In 2007, the UK experienced its first bank run of any significance since the reign of Queen Victoria as discussed by the authors, and unlike most runs in banking history, it was a run only on a bank called Northern Rock.
Abstract: In autumn of 2007 Britain experienced its first bank run of any significance since the reign of Queen Victoria. The run was on a bank called Northern Rock. This was extraordinary, for Britain had been free of such episodes because by early in the third quarter of the 19th century the Bank of England had developed techniques to prevent them. A second extraordinary aspect of the affair was that it was the decision to provide support for the troubled institution that triggered the run. And thirdly, unlike most runs in banking history, it was a run only on that one institution. This paper considers why the traditional techniques for the maintenance of banking stability failed - if they did fail - and then considers how these techniques may need to be changed or supplemented to prevent such problems in the future. The paper starts with a narrative of the events, then turns to banking policy before the event and to the policy responses after it. We suggest both why the decision to provide support triggered the run and why the run was confined to a single institution. That prepares the way for our consideration of what should be done to help prevent the recurrence of such episodes in the future.

32 citations

Journal Article•DOI•
Central Bank Institutional Structure and Effective Central Banking: Cross-Country Empirical Evidence

[...]

Iftekhar Hasan1, Iftekhar Hasan2, Loretta J. Mester3, Loretta J. Mester4•
Rensselaer Polytechnic Institute1, Bank of Finland2, Federal Reserve Bank of Philadelphia3, University of Pennsylvania4
19 Dec 2008-Comparative Economic Studies
TL;DR: In this article, the authors investigate the hypothesis that institutional form is related to performance of central banks and conclude that institutional forms play an important role in central bank performance, but little empirical work has been done to investigate this hypothesis.
Abstract: Over the last decade, the legal and institutional frameworks governing central banks and financial market regulatory authorities throughout the world have undergone significant changes. This has created a new interest in better understanding the roles played by organisational structures, accountability, and transparency in increasing the efficiency and effectiveness of central banks in achieving their objectives and ultimately yielding better economic outcomes. Although much has been written pointing out the potential role that an institutional form can play in central bank performance, little empirical work has been done to investigate the hypothesis that institutional form is related to performance. This paper attempts to help fill this void.

27 citations

Journal Article•DOI•
Shattered on the Rock? British financial stability from 1866 to 2007

[...]

Alistair Milne, Geoffrey Wood
25 Feb 2009-Journal of Banking Regulation
TL;DR: In this paper, the authors provide an answer to the basic question of why in the United Kingdom the traditional techniques for the maintenance of banking stability appeared to fail in the Northern Rock episode, and also consider how the techniques may need to be changed or supplemented to prevent such problems in the future.
Abstract: This paper provides an answer to the basic question of why in the United Kingdom the traditional techniques for the maintenance of banking stability appeared to fail in the Northern Rock episode. It also considers how the techniques may need to be changed or supplemented to prevent such problems in the future. We propose the following actions to make the banking system robust. First, there should be arrangements for prompt and orderly closure of a bank as it approaches problems, before it would otherwise be forced to close by either insolvency or illiquidity. Second, there should be reform of deposit insurance, such that whatever sum is guaranteed is completely guaranteed, and can be accessed without any significant delay. Third, arrangements need to be made such that customers retain access to all core banking services either through speedy transfer of all accounts or the continued operation in some guise of the troubled bank.

24 citations

References
More filters
Journal Article•DOI•
Optimum consumption and portfolio rules in a continuous-time model☆

[...]

Robert C. Merton1•
Massachusetts Institute of Technology1
01 Dec 1971-Journal of Economic Theory
TL;DR: In this paper, the authors considered the continuous-time consumption-portfolio problem for an individual whose income is generated by capital gains on investments in assets with prices assumed to satisfy the geometric Brownian motion hypothesis, which implies that asset prices are stationary and lognormally distributed.
Abstract: Publisher Summary A common hypothesis about the behavior of limited liability asset prices in perfect markets is the random walk of returns or in its continuous-time form the geometric Brownian motion hypothesis, which implies that asset prices are stationary and log-normally distributed. A number of investigators of the behavior of stock and commodity prices have questioned the accuracy of the hypothesis. In an earlier study described in the chapter, it was examined that the continuous-time consumption-portfolio problem for an individual whose income is generated by capital gains on investments in assets with prices assumed to satisfy the “geometric Brownian motion” hypothesis. Under the additional assumption of a constant relative or constant absolute risk-aversion utility function, explicit solutions for the optimal consumption and portfolio rules were derived. The changes in these optimal rules with respect to shifts in various parameters such as expected return, interest rates, and risk were examined by the technique of comparative statics. This chapter presents an extension of these results for more general utility functions, price behavior assumptions, and income generated also from noncapital gains sources. If the geometric Brownian motion hypothesis is accepted, then a general separation or mutual fund theorem can be proved such that, in this model, the classical Tobin mean-variance rules hold without the objectionable assumptions of quadratic utility or of normality of distributions for prices. Hence, when asset prices are generated by a geometric Brownian motion, the two-asset case can be worked on without loss of generality.

4,952 citations

Additional excerpts

  • ...We follow Baksi and Chen (1996), Merton (1971) and Grossman and Grossmann and Shiller (1982) by assuming ∆pi,t pi,t = µei,t∆t + σ e i,tΩ e i,t √ ∆t (37) where µei,t and σ e i,t are, respectively, the conditional expected value and the standard deviation of real return on asset i per unit of time....

    [...]

Book Chapter•DOI•
Optimum Consumption and Portfolio Rules in a Continuous-Time Model*

[...]

Robert C. Merton1•
Massachusetts Institute of Technology1
01 Jan 1975
TL;DR: In this paper, the authors considered the continuous-time consumption-portfolio problem for an individual whose income is generated by capital gains on investments in assets with prices assumed to satisfy the geometric Brownian motion hypothesis, which implies that asset prices are stationary and lognormally distributed.
Abstract: Publisher Summary A common hypothesis about the behavior of limited liability asset prices in perfect markets is the random walk of returns or in its continuous-time form the geometric Brownian motion hypothesis, which implies that asset prices are stationary and log-normally distributed. A number of investigators of the behavior of stock and commodity prices have questioned the accuracy of the hypothesis. In an earlier study described in the chapter, it was examined that the continuous-time consumption-portfolio problem for an individual whose income is generated by capital gains on investments in assets with prices assumed to satisfy the “geometric Brownian motion” hypothesis. Under the additional assumption of a constant relative or constant absolute risk-aversion utility function, explicit solutions for the optimal consumption and portfolio rules were derived. The changes in these optimal rules with respect to shifts in various parameters such as expected return, interest rates, and risk were examined by the technique of comparative statics. This chapter presents an extension of these results for more general utility functions, price behavior assumptions, and income generated also from noncapital gains sources. If the geometric Brownian motion hypothesis is accepted, then a general separation or mutual fund theorem can be proved such that, in this model, the classical Tobin mean-variance rules hold without the objectionable assumptions of quadratic utility or of normality of distributions for prices. Hence, when asset prices are generated by a geometric Brownian motion, the two-asset case can be worked on without loss of generality.

2,644 citations

Journal Article•DOI•
An intertemporal general equilibrium model of asset prices

[...]

John C. Cox, Jonathan E. Ingersoll, Stephen A. Ross
01 Mar 1985-Econometrica
TL;DR: In this paper, a continuous time general equilibrium model of a simple but complete economy is developed to examine the behavior of asset prices and their stochastic properties are determined endogenously, and the model is fully consistent with rational expectations and maximizing behavior on the part of all agents.
Abstract: This paper develops a continuous time general equilibrium model of a simple but complete economy and uses it to examine the behavior of asset prices. In this model, asset prices and their stochastic properties are determined endogenously. One principal result is a partial differential equation which asset prices must satisfy. The solution of this equation gives the equilibrium price of any asset in terms of the underlying real variables in the economy. IN THIS PAPER, we develop a general equilibrium asset pricing model for use in applied research. An important feature of the model is its integration of real and financial markets. Among other things, the model endogenously determines the stochastic process followed by the equilibrium price of any financial asset and shows how this process depends on the underlying real variables. The model is fully consistent with rational expectations and maximizing behavior on the part of all agents. Our framework is general enough to include many of the fundamental forces affecting asset markets, yet it is tractable enough to be specialized easily to produce specific testable results. Furthermore, the model can be extended in a number of straightforward ways. Consequently, it is well suited to a wide variety of applications. For example, in a companion paper, Cox, Ingersoll, and Ross [7], we use the model to develop a theory of the term structure of interest rates. Many studies have been concerned with various aspects of asset pricing under uncertainty. The most relevant to our work are the important papers on intertemporal asset pricing by Merton [19] and Lucas [16]. Working in a continuous time framework, Merton derives a relationship among the equilibrium expected rates of return on assets. He shows that when investment opportunities are changing randomly over time this relationship will include effects which have no analogue in a static one period model. Lucas considers an economy with homogeneous individuals and a single consumption good which is produced by a number of processes. The random output of these processes is exogenously determined and perishable. Assets are defined as claims to all or a part of the output of a process, and the equilibrium determines the asset prices. Our theory draws on some elements of both of these papers. Like Merton, we formulate our model in continuous time and make full use of the analytical tractability that this affords. The economic structure of our model is somewhat similar to that of Lucas. However, we include both endogenous production and

1,999 citations

Journal Article•DOI•
Equilibria under ‘active’ and ‘passive’ monetary and fiscal policies

[...]

Eric M. Leeper1•
Federal Reserve System1
01 Feb 1991-Journal of Monetary Economics
TL;DR: In this paper, monetary and fiscal policy interactions are studied in a stochastic maximizing model, where policy is either passive or active depending on its responsiveness to government debt shocks, and the existence and uniqueness of equilibria depend on two policy parameters.
Abstract: Monetary and fiscal policy interactions are studied in a stochastic maximizing model. Policy is ‘active’ or ‘passive’ depending on its responsiveness to government debt shocks. Schemes for financing deficits and, therefore, the existence and uniqueness of equilibria depend on two policy parameters. The model is used to: (i) characterize the equilibria implied by various financing schemes, (ii) derive policies where fiscal behavior determines how monetary shocks affect prices, and (iii) reinterpret Friedman's 1948 policy framework. The paper reconsiders the result that prices are indeterminate when the nominal interest rate is pegged. The setup can be used to interpret reduced-form studies on fiscal financing.

1,884 citations

"A continuous-time model of the term..." refers background in this paper

  • ...The theory of price level determination advocated by Leeper (1991), Sims (1994), Woodford (1996) and Cochrane (1998) has brought to the attention of macroeconomists the role of interactions between fiscal and monetary policy....

    [...]

  • ...We follow Baksi and Chen (1996), Merton (1971) and Grossman and Grossmann and Shiller (1982) by assuming...

    [...]

  • ...We think of ‘interactions’ in the sense captured by the “fiscal theory of the price level” of Leeper (1991), Sims (1994), Woodford (1996), and recently extended by Cochrane (1998, 1999), which suggests that a tight fiscal policy is a necessary complement to ensure price stability....

    [...]

Journal Article•DOI•
A simple model for study of the determination of the price level and the interaction of monetary and fiscal policy

[...]

Christopher A. Sims1•
Yale University1
01 May 1994-Economic Theory
TL;DR: In this paper, a representative agent model with money holdings motivated by transactions costs, a fiscal authority that taxes and issues debt, no production, and a convenient functional form for agents' utility is presented.
Abstract: A representative-agent model with money holdings motivated by transactions costs, a fiscal authority that taxes and issues debt, no production, and a convenient functional form for agents' utility is presented. The model can be solved analytically, and illustrates the dependence of price determination on fiscal policy, the possibility of indeterminacy, even stochastic explosion, of the price level in the face of a monetary policy that holdsM fixed, and the possibility of a unique, stable price level in the face of a monetary policy that simply pegs the nominal interest rate at an arbitrary level. In a rational expectations, market-clearing equilibrium model with a costlessly-produced fiat money that is useful in transactions, the following things are true under broad assumptions. - A monetary policy that fixes the money stock may (depending on the transactions technology) be consistent with indeterminacy of the price level—indeed with stochastically fluctuating, explosive inflation. - A monetary policy that fixes the nominal interest rate, even if it holds the interest rate constant regardless of the observed rate of inflation or money growth rate, may deliver a uniquely determined price level. - The existence and uniqueness of the equilibrium price level cannot be determined from knowledge of monetary policy alone; fiscal policy plays an equally important role. Special case models with interest-bearing debt and no money are possible, just as are special cases with money and no interest-bearing debt. In each the price level may be uniquely determined. Determinacy of the price level under any policy depends on the public's beliefs about what the policy authority would do under conditions that are never observed in equilibrium. These points are not new. Eric Leeper [1991] has made most of them within a single coherent model. Woodford [1993], in a representative agent cash-in-advance model, has displayed the possibility of indeterminacy with a fixed quantity of money and the possibility of uniqueness with an interest-rate pegging policy. Aiyagari and Gertler [1985] use an overlapping generations model to make many of the points made in this paper, without discussing the possibility of stochastic sunspot equilibria. Sargent and Wallace [1981] and Obstfeld [1983] have also discussed related issues. This paper improves on Leeper by moving beyond his analysis of local linear approximations to the full model solution, as is essential if explosive sunspot equilibria are to be distinguished from explosive solutions to the Euler equations that can be ruled out as equilibria. It improves on the other cited work by pulling together into the context of one fairly transparent model discussion of phenomena previously discussed in isolation in very different models. We study a representative agent model in which there is no production or real savings, but transactions costs generate a demand for money. The government costlessly provides fiat money balances, imposes lump-sum taxes, and issues debt, but has no other role in the economy. We make restrictive assumptions about the form of the utility function and the form of a transactions cost term in the budget constraint. The model could be extended to include production, capital accumulation, non-neutral taxation, productive government expenditure, and a more general utility function without affecting the conclusions discussed in this paper. Indeed the model I informally matched to data in an earlier paper [1988] makes some such extensions. While such an extended model is more realistic, it is harder to solve. The version in my earlier paper [1988] was solved numerically and simulated. The bare-bones model of this paper allows an explicit analytic solution that may make its results easier to understand.

892 citations

"A continuous-time model of the term..." refers background in this paper

  • ...The theory of price level determination advocated by Leeper (1991), Sims (1994), Woodford (1996) and Cochrane (1998) has brought to the attention of macroeconomists the role of interactions between fiscal and monetary policy....

    [...]

  • ...A bound on φ1 can be established from Sims (1994) by setting φ1 at a value lower than or equal to the discount factor β....

    [...]

  • ...We think of ‘interactions’ in the sense captured by the “fiscal theory of the price level” of Leeper (1991), Sims (1994), Woodford (1996), and recently extended by Cochrane (1998, 1999), which suggests that a tight fiscal policy is a necessary complement to ensure price stability....

    [...]

Related Papers (5)
On the Importance of Borrowing Constraints for House Price Dynamics

[...]

01 Jan 2008-Social Science Research Network
Essi Eerola, Essi Eerola, Niku Määttänen
Why do growth rates differ? Evidence from cross-country data on private sector production

[...]

01 Jul 2010-Empirica
Juha Kilponen, Matti Virén
Estimating open economy Phillips curves for the euro area with directly measured expectations

[...]

09 Nov 2009
Maritta Paloviita
Using financial markets information to identify oil supply shocks in a restricted VAR

[...]

18 Mar 2008-Research Papers in Economics
Marko Melolinna
Regulatory choices in global financial markets : restoring the role of aggregate utility in the shaping of market supervision

[...]

01 Jan 2008-Research Papers in Economics
Peik Granlund
Frequently Asked Questions (2)
Q1. What are the contributions mentioned in the paper "A continuous-time model of the term structure of interest rates with fiscal-monetary policy interactions" ?

The authors study the term structure implications of the fiscal theory of price level determination. The authors introduce the intertemporal budget constraint of the government in a general equilibrium model in continuous time. The authors show how to solve for the prices of real and nominal zero coupon bonds. 

A number of interesting avenues of future work can be considered. The model presented in this paper should be taken to the data to study how inflation risk premia are affected by fiscal determinants.