
A Genetic Algorithm for Simultaneous Localization and Mapping
Tom Duckett
Centre for Applied Autonomous Sensor Systems
Dept. of Technology,
¨
Orebro University
SE-70182
¨
Orebro, Sweden
http://www.aass.oru.se
Abstract—This paper addresses the problem of
simultaneous localization and mapping (SLAM) by
a mobile robot. The SLAM problem is defined as a
global optimization problem in which the objective is
to search the space of possible robot maps. A genetic al-
gorithm is described for solving this problem, in which
a population of candidate solutions is progressively
refined in order to find a globally optimal solution.
The fitness values in the genetic algorithm are obtained
with a heuristic function that measures the consistency
and compactness of the candidate maps. The results
show that the maps obtained are very accurate, though
the approach is computationally expensive. Directions
for future research are also discussed.
I. INTRODUCTION
Maps are very useful for navigation by mobile
robots in complex environments, being needed for
tasks such as self-localization, path planning, manip-
ulation of objects, and interaction with humans. To
navigate in unknown environments, an autonomous
robot requires the ability to build its own map while
simultaneously maintaining an estimate of its own
position. This is a hard problem because the same,
noisy sensor data must be used for both mapping and
localization. We can separate two major sources of
uncertainty in solving this problem:
(i.) the continuous uncertainty in the positions of the
vehicle and the observed environmental features
(e.g., due to sensor noise, uncertain execution of
motor commands, etc.), and
(ii.) the combinatorial labelling problem of data as-
sociation (e.g., landmark identification, feature
recognition, place recognition, etc.) in which a
correspondence must be found between sensor
measurements and the features already repre-
sented in the map.
Most current solutions to the SLAM problem con-
sider only the first type of uncertainty, and assume
that the data association problem is solved when
observations are integrated into the map (e.g., it is
typical to assume that all landmarks can be identified
uniquely). However, this assumption is bound to fail
sooner or later for robots operating in complex envi-
ronments. In short, data association failures produce
localization errors, which can lead to catastrophic
errors in the map. Without this assumption, the robot
must somehow search the space of possible maps,
since alternative assignments in data association can
induce very different maps.
In this paper, a new approach is proposed in which
SLAM is defined as a global optimization problem,
and the objective is to search the space of possible
robot trajectories. There is no explicit data associa-
tion or self-localization phase. Instead, the recorded
odometry data of the robot is used as a model from
which an initial population of possible trajectories
is randomly generated. Each of these trajectories is
then evaluated by constructing a global occupancy
map using the recorded range-finder data of the robot
along the travelled path. A fitness value is calculated
for each of the candidate solutions, based on the
consistency and compactness of the maps produced,
and the search proceeds using a genetic algorithm
(GA). GAs are a well-known search technique in
which simplified, numerical forms of the biological
processes of selection, inheritance and variation are
used to improve the average fitness of the population
through successive iterations [7].
The rest of this paper is structured as follows.
After a brief review of related work, SLAM is
defined as a global optimization problem (Section
3), followed by a description of the genetic algorithm
developed to solve it (Section 4). Experimental re-
sults using sensor data from a real robot are then
presented, followed by conclusions and suggestions
for future work.

II. RELATED WORK
A classical solution to the SLAM problem is the
Extended Kalman Filter (EKF), a linear recursive
filter that estimates the absolute position of the robot
and all of the landmarks in the map (see e.g., [2],
[5]). The EKF requires analytic models of the vehicle
motion and observations, it makes a number of
assumptions which are often violated in practice, and
it will fail whenever data association fails.
Nebot et al. [14] extended the EKF with a Monte
Carlo sampling technique for handling possible data
association errors. The EKF is used for normal
operation, only switching to the sampling technique
to resolve ambiguities in landmark identification,
e.g., when a large loop is to be closed. While this
approach may reduce the number of data association
errors, it does not preclude them in all situations.
Measurements for incorrectly identified landmarks
would still be integrated by the EKF, producing an
incorrect map.
Gutmann and Konolige [6] considered mapping
of large, circular environments using a combination
of topological and metric representations. An in-
cremental version of the Lu and Milios algorithm
for registration of laser scans [10] was first used
to find the most consistent metric representation
given the current topology. Then a global correlation
procedure [8] was used to detect when a previously
visited location had been reached. This would trigger
iteration of the local registration algorithm to obtain
a new metric map based on the corrected topology,
thus “closing the loop”. A drawback of this approach
is that false matches in the global registration proce-
dure could produce catastrophic mapping errors.
Thrun et al. [16] used an expectation maximization
(EM) algorithm for robot mapping, which alternates
between an ‘E-step’ that estimates the trajectory of
the robot given the current map and an ‘M-step’ that
estimates the map given the current trajectory. While
effective, this technique is basically a gradientbased
hill-climber or local optimization technique, so it de-
pends upon a good initial solution to avoid becoming
trapped in a local optimum.
Montemerlo et al. [11] introduced a hybrid ap-
proach using a particle filter to track the pose of
the robot, where each particle is associated with a
set of Kalman filters estimating the position for each
landmark. This approach has the advantage that it
is able to represent and search between multiple
hypotheses for the full map (i.e., each hypothesis
comprises the robot pose and all landmark positions).
It has the disadvantage that the particle set must be
large enough to include a particle sufficiently close
to the true pose of the robot at all times, which may
not be practical when closing very large loops.
III. SLAM AS A GLOBAL OPTIMIZATION
PROBLEM
In an optimization problem, the aim is to minimize
or maximize some objective function. In a global
optimization problem, there may be many solutions
which are locally optimal. The goal is to find the one
best solution, avoiding the local optima [15].
In this paper, SLAM is treated as a continuous
global optimization problem with the following ele-
ments:
(i.) The search is carried out in the space of possible
robot trajectories. A trajectory can be defined as
a vector [δ
1
, α
1
, ..., δ
N
, α
N
] where δ
j
and α
j
are
the relative distance and rotation travelled by the
robot in one small step j, and there are N steps
in total.
(ii.) The robot’s own measurements of its trajectory
are used as a generative model. In general, these
measurements will be corrupted by noise, e.g.,
due to odometer drift error. We use the recorded
odometry trace of the robot to generate candi-
date solutions by applying different correction
factors to the measured values of δ
j
and α
j
.
(iii.) Candidate solutions are coded as a vector of cor-
rection factors. The trajectory of the robot is first
divided into M segments, where M N in gen-
eral, in order to reduce the number of variables
optimized to a manageable level. One solu-
tion consists of a vector [∆δ
1
, ∆α
1
, ..., ∆δ
M
, ∆α
M
]
where ∆δ
k
, ∆α
k
are the correction factors ap-
plied to the distance and angle measurements
within one segment k. We assume that the
noise properties are uniform along the trajectory
within each segment.
(iv.) A set of allowed moves for generating new
solutions from previous ones is defined.
(v.) An evaluation function is used to assess the
quality of the candidate solutions. This is imple-
mented by inferring a map from each candidate
trajectory, then using a heuristic function to
assess the quality of the maps obtained.
With this approach, a global search algorithm can
be used to search the space of possible trajectories.

The goal is to find the vector of noise parameters, and
therefore the inferred trajectory, which produces the
best map. In this paper, the SLAM problem is thus
solved by a genetic algorithm, described as follows.
IV. THE GENETIC ALGORITHM
Genetic algorithms are a global search technique
which mimic aspects of biological evolution, namely
the process of natural selection and the principle
of “survival of the fittest”. They use an adaptive
search procedure based on a population of candidate
solutions or “chromosomes”. Each iteration or “gen-
eration” involves a competitive selection procedure
that favours fitter solutions and rejects poorer solu-
tions. The successful candidates are then recombined
with other solutions by swapping components with
one other; they can also be mutated by making a
small change to a single component. The procedure
is repeated for many generations, producing new
solutions that are biased towards regions of the
search space in which good solutions have already
been found.
A. Chromosome Encoding
Each chromosome is encoded as a string of float-
ing point numbers corresponding to the correction
factors applied to the recorded odometry data. In
the experiments presented here, the odometer trace
was divided into segments of 3 meters in length. For
the environment of Fig. 1, there were 50 segments
corresponding to the 150 meters travelled by the
robot.
For each segment k, the chromosome contains two
floating point numbers −d
max
≤ ∆δ
k
≤ +d
max
and
−a
max
≤ ∆α
k
≤ +a
max
that encode the correction
factors applied to the distance and angle measure-
ments respectively. That is, the measured values of
δ
j
and α
j
obtained from the robot’s odometry are
assumed to lie within a fixed range of their true
values (in the experiments presented here, a range of
±2% was assumed for both the distances and angles).
The initial population of chromosome is obtained
by randomly initializing the values of ∆δ
k
and ∆α
k
in this range. It would also be possible to assume
some parametric distribution (e.g., Gaussian) for the
correction factors during initialization.
B. Fitness Function
The fitness function contains domain specific
knowledge that is used to assess the quality of the
candidate solutions. An important property is that it
must be very fast, since it may be executed thousands
of times in one run of the algorithm.
In this paper, a much simplified version of the
occupancy grid model [12] is used to construct a map
for each candidate solution, then two heuristics are
combined to obtain a fitness value for each map. The
whole procedure runs in approximately 0.95 seconds
on a 200MHz Pentium II processor for one candidate
solution using the map data of Fig. 1 with 25971
readings from a SICK laser scanner (only 1 out of
every 5 readings is used in each scan, where the scans
are taken at intervals of 10 cm, and the remaining
readings are discarded). The procedure is described
as follows.
The recorded odometry data is corrected using
the correction factors encoded in the chromosome.
Then the corrected odometry is combined with the
recorded laser range-finder data of the robot to
build an occupancy grid with a resolution of 10 cm.
Because of the use of laser data, we do not need
complex ray or cone models; a simple line model is
sufficient. For each cell i in the grid, two quantities
are calculated: occ
i
, the number of laser readings
which indicate that the cell is occupied, and emp
i
,
the number of readings which indicate that the cell
is empty. The following heuristic functions are then
calculated:
1) Map Consistency (MC1): The idea here is
to measure the overall consistency of the sensory
information contained in the gridmap. We try to
measure the degree of disagreement or “conflict”
between the sensor readings. A similar metric was
proposed by Murphy et al. [13] based on Dempster-
Shafer theory. The measure is calculated as
MC
1
=
∑
i
min(occ
i
, emp
i
)
by taking the minimum of the occ
i
and emp
i
values
for all cells i.
2) Map Compactness (MC2): Early experiments
with the map consistency measure showed that the
genetic algorithm could produce maps with very low
conflict but which were obviously incorrect to the
human eye. The GA would try to avoid conflict –
rather than resolving it – by “twisting” certain critical
areas of the map away from one another, when the
represented regions were in fact physically adjacent
(see Fig. 2).
The idea here is to reward the GA for producing
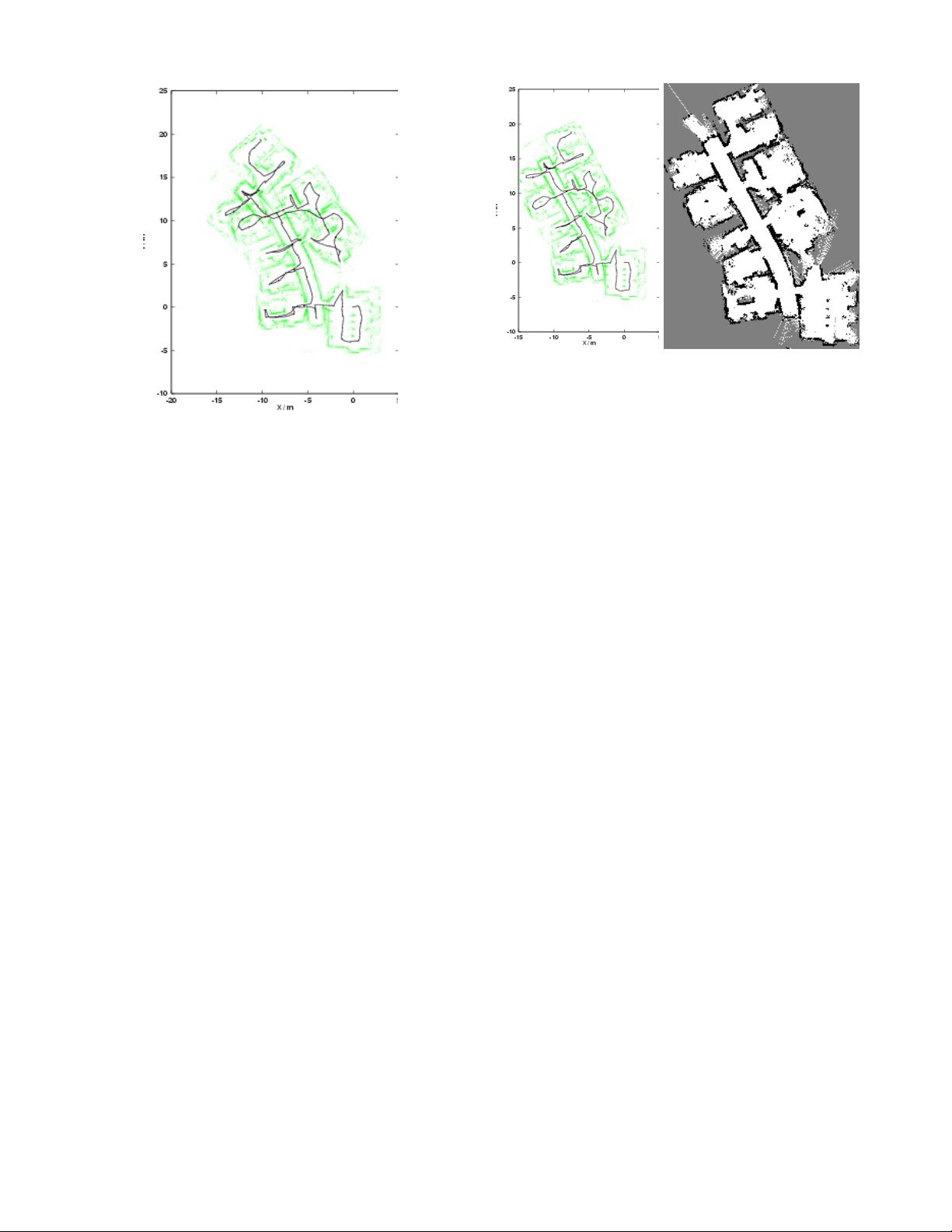
Fig. 1. Raw sensor data from the Artificial Intelligence Lab,
Freiburg, as in [6], showing the odometry trace and laser range-
finger readings.
smaller, more compact maps. This is done by fitting
a bounding box to the map that indicates the total
area covered by cells with occ
i
> 0. The measure is
calculated as
MC
2
= (x
max
− x
min
) × (y
max
− y
min
)
where x
max
and x
min
refer to the maximum and
minimum x-coordinates of the bounding box,
measured in number of grid cells.
Fitness Value: Finally, the two metrics are com-
bined as
F = MC
1
+ wMC
2
where the weight w = 0.3 determines the relative im-
portance of the two heuristics in the fitness function.
Note that better maps produce lower values of F.
C. Selection, Crossover and Mutation
The selection phase in a genetic algorithm involves
creating a “mating pool” by picking individual so-
lutions that are fitter with higher probability. The
selected individuals in the mating pool are then com-
bined to make a new population using the crossover
operator, with occasional small random changes due
to the mutation operator, described as follows.
In the GA presented here, the population is first
sorted according to the values produced by the fitness
function. Individuals are then assigned an offspring
count that is solely a function of their rank, using the
scheme proposed by Baker [1]. In this method, each
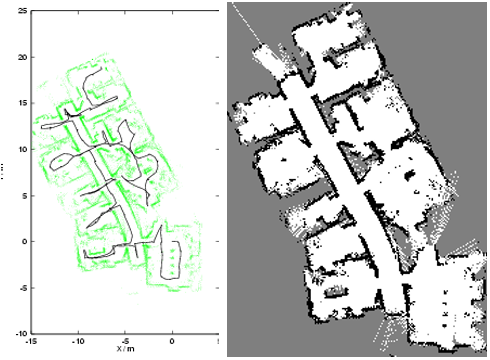
Fig. 2. Corrected sensor data obtained using only the fitness
function F = MC
1
and the corresponding gridmap.
string l is assigned an expected offspring count e
l
.
The fittest individual is assigned a value of e
l
= λ
max
,
the weakest individual is assigned a value of e
l
=
λ
min
, and the other members of the population are as-
signed an intermediate value by linear interpolation.
In this paper, values of λ
max
= 1.5 and λ
min
= 0.5
were used.
The standard selection method in a GA is the
weighted roulette wheel [7]. However, this scheme
has the problem that the best individuals may fail
to produce offspring in the next generation, resulting
in a so-called stochastic error [9]. Instead, a scheme
known as Remainder Stochastic Sampling Without
Replacement is used. Each individual is first allo-
cated offspring according to the integer part of e
l
in completely deterministic fashion. The remaining
strings needed to fill out the population are then
obtained randomly by generating new offspring for
each string with probability equal to the fractional
part of e
l
. “Without replacement” means that strings
can only be selected once in the non-deterministic
phase, so that a string with e
l
= 1.5 would receive
either 1 or 2 offspring in total.
Pairs of selected strings are then combined by
crossover. Multiple crossover sites are used, so that
the encoded values in the two mating strings are
completely mixed up in the two strings produced.
This is achieved by randomly choosing between
the two parents at each site in the chromosome.
Crossover is carried out with probability p = 0.85,
otherwise the selected strings are left unchanged.
Mutation is carried out by picking single values

Fig. 3. Corrected sensor data obtained using the full fitness
function F = MC
1
+ wMC
2
and the corresponding gridmap.
within the strings with very low probability p =
0.005 and replacing those values with randomly
generated values, as upon initialization.
V. EXPERIMENTAL RESULTS
The algorithm was first tested using data recorded
by a Pioneer I mobile robot equipped with a SICK
laser scanner at the Artificial Intelligence Lab of the
University of Freiburg [6]. The raw sensor data is
shown in Fig. 1. The genetic algorithm was run for
150 generations with a population size of 50, i.e., a
total of 7500 candidate maps were evaluated, taking
around 2 hours on a 200MHz Pentium II processor.
Fig. 4 shows the resulting fitness values produced, il-
lustrating the convergence of the algorithm over time.
The corrected sensor data obtained from the fittest
solution, together with the corresponding gridmap,
is shown in Fig. 3.
VI. CONCLUSIONS AND FUTURE WORK
The major contribution of this paper is that the
problem of simultaneous localization and mapping
(SLAM) has been defined for the first time as a
global optimization problem. A genetic algorithm
was developed to solve this problem, producing a
global solution by searching the space of possible
robot maps.
Genetic algorithms are particularly useful for solv-
ing environment modelling problems because they
Fig. 4. Fitness values over time for the genetic algorithm using
the data of Fig. 1, showing the fitness of both the best and median
members of the population in each generation.
exploit the building block hypothesis, whereby better
and better strings are constructed from the best
partial solutions (i.e., schemata or building blocks)
of previous generations [4]. Most real world envi-
ronments can be decomposed spatially into natu-
ral building blocks such as rooms, corridors, open
spaces, etc.
A major benefit of the approach is that it makes
very few assumptions about the underlying problem,
and the only critical parameter is the weighting
between the consistency and compactness heuristics
in the fitness function. A disadvantage of the ap-
proach at present is that it requires large amounts of
computation.
There are other possible algorithms for performing
global optimization [15], such as branch and bound
algorithms, simulated annealing, etc., which should
also be investigated. A further possibility would be
to combine the global search algorithm with a local
optimization method, e.g., EKF [5], consistent pose
estimation [10], relaxation [3], etc. In the case of
the GA, this could dramatically reduce the overall
computation time.
Another important direction is to implement an on-
line version of the algorithm suitable for use in real-
time on a self-navigating mobile robot. This would
involve continually searching the space of possible
maps while the robot is in motion, automatically ex-
tending the candidate maps with the incoming sensor
information. The current best map would be used
for decision making, e.g., path planning. A further
possibility would be to investigate implementation
of the algorithm on parallel processors, given the
parallel nature of evolutionary computation.


![Fig. 1. Raw sensor data from the Artificial Intelligence Lab, Freiburg, as in [6], showing the odometry trace and laser rangefinger readings.](/figures/fig-1-raw-sensor-data-from-the-artificial-intelligence-lab-nuy0b1il.png)