Neural Processing Letters 9: 293–300, 1999.
© 1999 Kluwer Academic Publishers. Printed in the Netherlands.
293
Least Squares Support Vector Machine Classifiers
J.A.K. SUYKENS and J. VANDEWALLE
Katholieke Universiteit Leuven, Department of Electrical Engineering, ESAT-SISTA Kardinaal
Mercierlaan 94, B–3001 Leuven (Heverlee), Belgium, e-mail: johan.suykens@esat.kuleuven.ac.be
Abstract. In this letter we discuss a least squares version for support vector machine (SVM) classi-
fiers. Due to equality type constraints in the formulation, the solution follows from solving a set of
linear equations, instead of quadratic programming for classical SVM’s. The approach is illustrated
on a two-spiral benchmark classification problem.
Key words: classification, support vector machines, linear least squares, radial basis function kernel
Abbreviations: SVM – Support Vector Machines; VC – Vapnik-Chervonenkis; RBF – Radial Basis
Function
1. Introduction
Recently, support vector machines (Vapnik, 1995; Vapknik, 1998a; Vapnik, 1998b)
have been introduced for solving pattern recognition problems. In this method one
maps the data into a higher dimensional input space and one constructs an optimal
separating hyperplane in this space. This basically involves solving a quadratic
programming problem, while gradient based training methods for neural network
architectures on the other hand suffer from the existence of many local minima
(Bishop, 1995; Cherkassky & Mulier, 1998; Haykin, 1994; Zurada, 1992). Kernel
functions and parameters are chosen such that a bound on the VC dimension is
minimized. Later, the support vector method was extended for solving function es-
timation problems. For this purpose Vapnik’s epsilon insensitive loss function and
Huber’s loss function have been employed. Besides the linear case, SVM’s based
on polynomials, splines, radial basis function networks and multilayer perceptrons
have been successfully applied. Being based on the structural risk minimization
principle and capacity concept with pure combinatorial definitions, the quality and
complexity of the SVM solution does not depend directly on the dimensionality of
the input space (Vapnik, 1995; Vapknik, 1998a; Vapnik, 1998b).
In this paper we formulate a least squares version of SVM’s for classification
problems with two classes. For the function estimation problem a support vec-
tor interpretation of ridge regression (Golub & Van Loan, 1989) has been given
in (Saunders et al., 1998), which considers equality type constraints instead of
inequalities from the classical SVM approach. Here, we also consider equality

294 J.A.K. SUYKENS AND J. VANDEWALLE
constraints for the classification problem with a formulation in least squares sense.
As a result the solution follows directly from solving a set of linear equations,
instead of quadratic programming. While in classical SVM’s many support values
are zero (nonzero values correspond to support vectors), in least squares SVM’s
the support values are proportional to the errors.
This paper is organized as follows. In Section 2 we review some basic work
about support vector machine classifiers. In Section 3 we discuss the least squares
support vector machine classifiers. In Section 4 examples are given to illustrate the
support values and on a two-spiral benchmark problem.
2. Support Vector Machines for Classification
In this Section we shortly review some basic work on support vector machines
(SVM) for classification problems. For all further details we refer to (Vapnik, 1995;
Vapnik, 1998a; Vapnik, 1998b).
Given a training set of N data points {y
k
,x
k
}
N
k=1
,wherex
k
∈ R
n
is the kth input
pattern and y
k
∈ R is the kth output pattern, the support vector method approach
aims at constructing a classifier of the form:
y(x) = sign
"
N
X
k=1
α
k
y
k
ψ(x, x
k
) + b
#
, (1)
where α
k
are positive real constants and b is a real constant. For ψ(·, ·) one typically
has the following choices: ψ(x, x
k
) = x
T
k
x (linear SVM); ψ(x, x
k
) = (x
T
k
x + 1)
d
(polynomial SVM of degree d); ψ(x, x
k
) = exp{−kx − x
k
k
2
2
/σ
2
} (RBF SVM);
ψ(x, x
k
) = tanh[κ x
T
k
x+θ] (two layer neural SVM), where σ, κ and θ are constants.
The classifier is constructed as follows. One assumes that
w
T
ϕ(x
k
) + b ≥ 1 , if y
k
=+1,
w
T
ϕ(x
k
) + b ≤−1 , if y
k
=−1,
(2)
which is equivalent to
y
k
[w
T
ϕ(x
k
) + b]≥1,k= 1, ..., N, (3)
where ϕ(·) is a nonlinear function which maps the input space into a higher di-
mensional space. However, this function is not explicitly constructed. In order to
have the possibility to violate (3), in case a separating hyperplane in this higher
dimensional space does not exist, variables ξ
k
are introduced such that
y
k
[w
T
ϕ(x
k
) + b]≥1 − ξ
k
,k= 1, ..., N,
ξ
k
≥ 0,k= 1, ..., N.
(4)
According to the structural risk minimization principle, the risk bound is minim-
ized by formulating the optimization problem
min
w,ξ
k
J
1
(w, ξ
k
) =
1
2
w
T
w + c
N
X
k=1
ξ
k
(5)

LEAST SQUARES SUPPORT VECTOR MACHINE CLASSIFIERS 295
subject to (4). Therefore, one constructs the Lagrangian
L
1
(w, b, ξ
k
; α
k
, ν
k
) = J
1
(w, ξ
k
) −
P
N
k=1
α
k
{y
k
[w
T
ϕ(x
k
) + b]−
−1 + ξ
k
}−
P
N
k=1
ν
k
ξ
k
(6)
by introducing Lagrange multipliers α
k
≥ 0, ν
k
≥ 0 (k = 1, ..., N ). The solution
is given by the saddle point of the Lagrangian by computing
max
α
k
,ν
k
min
w,b,ξ
k
L
1
(w, b, ξ
k
; α
k
, ν
k
). (7)
One obtains
∂L
1
∂w
= 0 → w =
P
N
k=1
α
k
y
k
ϕ(x
k
),
∂L
1
∂b
= 0 →
P
N
k=1
α
k
y
k
= 0,
∂L
1
∂ξ
k
= 0 → 0 ≤ α
k
≤ c, k = 1, ..., N,
(8)
which leads to the solution of the following quadratic programming problem
max
α
k
Q
1
(α
k
; ϕ(x
k
)) =−
1
2
N
X
k,l=1
y
k
y
l
ϕ(x
k
)
T
ϕ(x
l
) α
k
α
l
+
N
X
k=1
α
k
, (9)
such that
N
X
k=1
α
k
y
k
= 0, 0 ≤ α
k
≤ c, k = 1, ..., N.
The function ϕ(x
k
) in (9) is related then to ψ(x, x
k
) by imposing
ϕ(x)
T
ϕ(x
k
) = ψ(x, x
k
), (10)
which is motivated by Mercer’s Theorem. Note that for the two layer neural SVM,
Mercer’s condition only holds for certain parameter values of κ and θ.
The classifier (1) is designed by solving
max
α
k
Q
1
(α
k
; ψ(x
k
,x
l
)) =−
1
2
N
X
k,l=1
y
k
y
l
ψ(x
k
,x
l
) α
k
α
l
+
N
X
k=1
α
k
, (11)
subject to the constraints in (9). One does not have to calculate w nor ϕ(x
k
) in order
to determine the decision surface. Because the matrix associated with this quadratic
programming problem is not indefinite, the solution to (11) will be global (Fletcher,
1987).
Furthermore, one can show that hyperplanes (3) satisfying the constraint kwk
2
≤
a have a VC-dimension h which is bounded by
h ≤ min([r
2
a
2
],n)+ 1, (12)

296 J.A.K. SUYKENS AND J. VANDEWALLE
where [.] denotes the integer part and r is the radius of the smallest ball containing
the points ϕ(x
1
), ..., ϕ(x
N
). Finding this ball is done by defining the Lagrangian
L
2
(r, q, λ
k
) = r
2
−
N
X
k=1
λ
k
(r
2
−kϕ(x
k
) − qk
2
2
), (13)
where q is the center of the ball and λ
k
are positive Lagrange multipliers. In a
similar way as for (5) one finds that the center is equal to q =
P
k
λ
k
ϕ(x
k
),where
the Lagrange multipliers follow from
max
λ
k
Q
2
(λ
k
; ϕ(x
k
)) =−
N
X
k,l=1
ϕ(x
k
)
T
ϕ(x
l
) λ
k
λ
l
+
N
X
k=1
λ
k
ϕ(x
k
)
T
ϕ(x
k
), (14)
such that
N
X
k=1
λ
k
= 1, λ
k
≥ 0 ,k = 1, ..., N.
Based on (10), Q
2
can also be expressed in terms of ψ(x
k
,x
l
). Finally, one
selects a support vector machine with minimal VC dimension by solving (11) and
computing (12) from (14).
3. Least Squares Support Vector Machines
Here we introduce a least squares version to the SVM classifier by formulating the
classification problem as
min
w,b,e
J
3
(w,b,e) =
1
2
w
T
w + γ
1
2
N
X
k=1
e
2
k
, (15)
subject to the equality constraints
y
k
[w
T
ϕ(x
k
) + b]=1 − e
k
,k= 1, ..., N. (16)
One defines the Lagrangian
L
3
(w,b,e; α) = J
3
(w,b,e)−
N
X
k=1
α
k
{y
k
[w
T
ϕ(x
k
) + b]−1 + e
k
}, (17)
where α
k
are Lagrange multipliers (which can be either positive or negative now
due to the equality constraints as follows from the Kuhn-Tucker conditions (Fletcher,
1987)).
The conditions for optimality
∂L
3
∂w
= 0 → w =
P
N
k=1
α
k
y
k
ϕ(x
k
),
∂L
3
∂b
= 0 →
P
N
k=1
α
k
y
k
= 0,
∂L
3
∂e
k
= 0 → α
k
= γe
k
,k= 1, ..., N,
∂L
3
∂α
k
= 0 → y
k
[w
T
ϕ(x
k
) + b]−1 + e
k
= 0,k = 1, ..., N
(18)

LEAST SQUARES SUPPORT VECTOR MACHINE CLASSIFIERS 297
can be written immediately as the solution to the following set of linear equations
(Fletcher, 1987)
I 00
−Z
T
000 −Y
T
00γI −I
ZY I 0
w
b
e
α
=
0
0
0
E
1
, (19)
where Z =[ϕ(x
1
)
T
y
1
; ...; ϕ(x
N
)
T
y
N
], Y =[y
1
; ...; y
N
],
E
1 =[1; ...; 1], e =
[e
1
; ...; e
N
], α =[α
1
; ...; α
N
]. The solution is also given by
0
−Y
T
Y ZZ
T
+ γ
−1
I
b
α
=
0
E
1
. (20)
Mercer’s condition can be applied again to the matrix = ZZ
T
,where
kl
= y
k
y
l
ϕ(x
k
)
T
ϕ(x
l
)
= y
k
y
l
ψ(x
k
,x
l
).
(21)
Hence, the classifier (1) is found by solving the linear set of Equations (20)–(21)
instead of quadratic programming. The parameters of the kernels such as σ for
the RBF kernel can be optimally chosen according to (12). The support values α
k
are proportional to the errors at the data points (18), while in the case of (14) most
values are equal to zero. Hence, one could rather speak of a support value spectrum
in the least squares case.
4. Examples
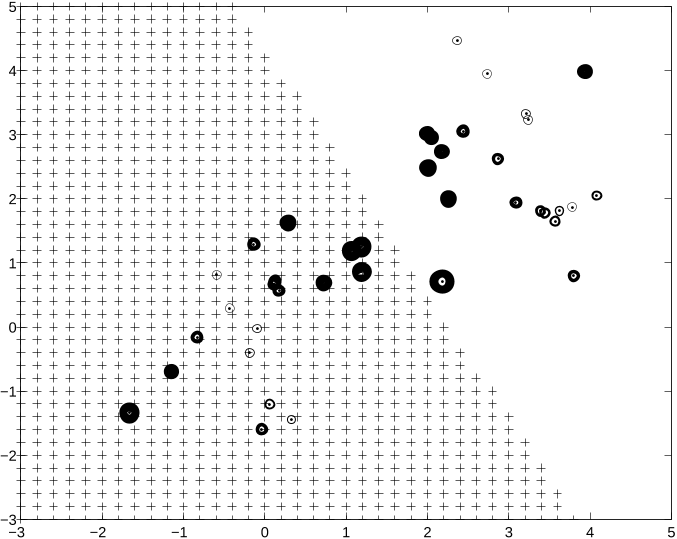
In a first example (Figure 1) we illustrate the support values for a linearly separable
problem of two classes in a two dimensional space. The size of the circles indicated
at the training data is chosen proportionally to the absolute values of the support
values. A linear SVM has been taken with γ = 1. Clearly, points located close and
far from the decision line have the largest support values. This is different from
SVM’s based on inequality constraints, where only points that are near the decision
line have nonzero support values. This can be understood from the fact that the
signed distance from a point x
k
to the decision line is equal to (w
T
x
k
+ b)/kwk=
(1 − e
k
)/(y
k
kwk) and α
k
= γe
k
in the least squares SVM case.
In a second example (Figure 2) we illustrate a least squares support vector
machine RBF classifier on a two-spiral benchmark problem. The training data are
shown on Figure 2 with two classes indicated by ’o’ and
0
∗
0
(360 points with 180
for each class) in a two dimensional input space. Points in between the training
data located on the two spirals are often considered as test data for this problem but
are not shown on the figure. The excellent generalization performance is clear from
the decision boundaries shown on the figures. In this case σ = 1andγ = 1were
chosen as parameters. Other methods which have been applied to the two-spiral