![Fig. 3. Performance of the quantum and classical noise radars in terms of the cross-correlation coefficient. (Upper) The cross-correlation coefficients for the quantum and classical noise radars, as functions of the transmitted quanta, rescaled such that √ η = 1. (Lower) The quantum advantage for the cases considered above. In both plots, we have considered the ξ = 10−3 and ξ = 0.5 settings. The first setting achieves a close to optimal cross-correlation coefficient. The second setting is suboptimal, and it has been used as classical reference in recent microwave illumination experiments [12], [13].](/figures/fig-3-performance-of-the-quantum-and-classical-noise-radars-ceuptaao.webp)
This is an electronic reprint of the original article.
This reprint may differ from the original in pagination and typographic detail.
Powered by TCPDF (www.tcpdf.org)
This material is protected by copyright and other intellectual property rights, and duplication or sale of all or
part of any of the repository collections is not permitted, except that material may be duplicated by you for
your research use or educational purposes in electronic or print form. You must obtain permission for any
other use. Electronic or print copies may not be offered, whether for sale or otherwise to anyone who is not
an authorised user.
Jonsson, Robert; Di Candia, Roberto; Ankel, Martin; Strom, Anders; Johansson, Goran
A comparison between quantum and classical noise radar sources
Published in:
2020 IEEE Radar Conference, RadarConf 2020
DOI:
10.1109/RadarConf2043947.2020.9266597
Published: 21/09/2020
Document Version
Peer reviewed version
Please cite the original version:
Jonsson, R., Di Candia, R., Ankel, M., Strom, A., & Johansson, G. (2020). A comparison between quantum and
classical noise radar sources. In 2020 IEEE Radar Conference, RadarConf 2020 [9266597] (IEEE Radar
Conference; Vol. 2020-September). IEEE. https://doi.org/10.1109/RadarConf2043947.2020.9266597
A comparison between quantum and classical noise
radar sources
Robert Jonsson
1
Department of Microtechnology
and Nanoscience
Chalmers University of Technology
2
Radar Solutions, Saab AB
G
¨
oteborg, Sweden
Email: robejons@chalmers.se
Anders Str
¨
om
Radar Solutions, Saab AB
G
¨
oteborg, Sweden
Roberto Di Candia
Department of Communications
and Networking
Aalto University
Helsinki, Finland
Email: roberto.dicandia@aalto.fi
G
¨
oran Johansson
Department of Microtechnology
and Nanoscience
Chalmers University of Technology
G
¨
oteborg, Sweden
Martin Ankel
1
Department of Microtechnology
and Nanoscience
Chalmers University of Technology
2
Radar Solutions, Saab AB
G
¨
oteborg, Sweden
Abstract—We compare the performance of a quantum radar
based on two-mode squeezed states with a classical radar system
based on correlated thermal noise. With a constraint of equal
number of photons N
S
transmitted to probe the environment, we
find that the quantum setup exhibits an advantage with respect
to its classical counterpart of
√
2 in the cross-mode correlations.
Amplification of the signal and the idler is considered at different
stages of the protocol, showing that no quantum advantage
is achievable when a large-enough gain is applied, even when
quantum-limited amplifiers are available. We also characterize
the minimal type-II error probability decay, given a constraint
on the type-I error probability, and find that the optimal decay
rate of the type-II error probability in the quantum setup
is ln(1 + 1/N
S
) larger than the optimal classical setup, in
the N
S
1 regime. In addition, we consider the Receiver
Operating Characteristic (ROC) curves for the scenario when the
idler and the received signal are measured separately, showing
that no quantum advantage is present in this case. Our work
characterizes the trade-off between quantum correlations and
noise in quantum radar systems.
I. INTRODUCTION
The quantum Illumination (QI) protocol [1]–[7] uses en-
tanglement as a resource to improve the detection of a low-
reflectivity object embedded in a bright environment. The
protocol was first developed for a single photon source [1],
and it was then extended to general bosonic quantum states
and thermal bosonic channels [2]. Here, a
6
dB advantage
in the effective signal-to-noise ratio (SNR) is achievable
when using two-mode squeezed states instead of coherent
states. This gain has been recently shown to be optimal,
and reachable exclusively in the regime of low transmitting
power per mode [8], [9]. The QI protocol has possible
applications in the spectrum below the Terahertz band, as
here the environmental noise is naturally bright. In particular,
microwave quantum technology has been very well developed
in the last decades [10], paving the way of implementing these
ideas for building a first prototype of quantum radar.
The possible benefits of a quantum radar system are generally
understood to be situational. In an adversarial scenario, it
is beneficial for a radar system to be able to operate while
minimizing the power output, in order to reduce the probability
for the transmitted signals to be detected. This property is
commonly referred to as Low Probability of Intercept (LPI),
and it is a common measure to limit the ability of the enemy
to localize and discover the radar. The low signal levels
required for QI are in principle excellent for acquiring good
LPI properties. However, there are several challenges to face
in order to achieve this goal. A first proposal for implementing
a microwave QI protocol was advanced in Ref. [11]. The
protocol relies on an efficient microwave-optical interface for
the idler storage and the measurement stage. This technology is
promising for this and other applications, however it is still in its
infancy. Furthermore, the signal generation requires cryogenic
technology, which must be interfaced with a room-temperature
environment. Recently, a number of QI-related experiments
have been carried out in the microwave regime [12], [13],
showing that some correlations of an entangled signal-idler
system are preserved after the signal is sent out of the dilution
refrigerator. While these results are a good benchmark for future
QI experiments, they strictly rely on the amplification of the
signal and idler. This has been shown to rule out any quantum
advantage with respect to an optimal classical reference [14].
In this work, we discuss the role of quantum correlations
and amplification in the QI protocol, providing a comparative
analysis of quantum and classical noise radars in different
scenarios. Noise radar is an old concept that operates by
probing the environment with a noisy signal and cross-
correlating the returns with a retained copy of the transmitted
signal [15]. A quantum noise radar operates similarly to its
conventional counterpart, but differs in the use of a two-mode
entangled state as noise source [12], [13]. An advantage of
the quantum noise radar over the classical counterpart can be
declared if stronger correlations can be achieved, when both
systems illuminate the environment with equal power. In the
microwave regime, the two-mode squeezed state used for noise
correlations can be generated with superconducting circuits with
a Josephson Parametric Amplifier (JPA) at
T ' 20
mK [16],
[17]. On the one hand, using quantum correlated signals
generated by a JPA enhances the signal-to-noise ratio in the
low transmitting power per mode regime. On the other hand,
Josephson parametric circuits are able to generate correlated
and entangled signals with large bandwidth [18]–[20]. This
allows, in principle, a system to operate in the low power-per-
mode regime, where quantum radars show fully their advantage.
Here, we analyze the performance of a JPA-based noise radar
in different scenarios which include different sources of noise.
Our analysis shows that any quantum advantage is destroyed
by the unavoidable noise added when amplifying either the
signal or the idler. We also show when the idler and signal are
measured separately, the entanglement initially present in the
signal-idler system is not properly exploited, and no quantum
advantage can be retained. The latter happens even without
amplifying the signal or the idler. Our work complements the
analysis done in Ref. [14] with the explicit calculations of the
cross-correlation coefficients and the optimal asymptotic ROC
performance in the microwave regime.
II. THEORY
In this section, we introduce the models for the quantum and
classical systems, within the quantum mechanical description.
In this step, we emulate Refs. [14], [21], where the classical
and quantum noise radar were first studied. In all expressions,
we assume the natural units (~ = 1, k
B
= 1).
A. Quantum preliminaries
A single, narrowband mode of the electric field, at microwave
frequency
f
, is defined with an operator (in suitable units)
as
ˆ
E = ˆq cos 2πft + ˆp sin 2πft,
where
ˆq
and
ˆp
are the in-
phase and quadrature operators, respectively. The quadratures
are related to the bosonic annihilation (
ˆa
) and creation (
ˆa
†
)
operators as
ˆq = (ˆa
†
+ˆa)/
√
2
and
ˆp = i(ˆa
†
−ˆa)/
√
2
, where
[ˆa, ˆa
†
] =
ˆ
I
. The commutation relation
[ˆq, ˆp] = i
ˆ
I
implies
that the quadratures can not be measured simultaneously with
arbitrary precision, due to the Heisenberg uncertainty relation.
In the following, we represent the quadratures of the two-
modes of the electric field by the vector
ˆ
X = (ˆq
S
, ˆp
S
, ˆq
I
, ˆp
I
)
T
,
where the indices S and I refer to the signal and idler mode,
respectively. These mode designations are used interchangeably
for both the quantum and classical system.
1) Classically-correlated thermal noise: The classically-
correlated noise (CCN) system uses two sources of thermal
noise,
ˆa
0
and
ˆa
1
, at temperatures
T
0
and
T
1
, respectively.
T
1
T
0
(ξ, ϕ)
ˆa
0
ˆa
1
ˆa
(C)
S
ˆa
(C)
I
Fig. 1.
Preparation of classically-correlated thermal noise.
A beamsplitter
with reflection coefficient
ξ
and phase turning angle
ϕ
generates the signal
and idler modes from the modes
ˆa
0
and
ˆa
1
. These modes are in a thermal
state with
T
0
and
T
1
effective noise temperatures, respectively. The output
modes are correlated provided that T
0
6= T
1
.
In general, the quantum state of a thermal noise mode at
temperature T can be represented by the density operator
ρ
th
=
∞
X
n=0
N
n
(N + 1)
n+1
|nihn|, (1)
where the average number
1
of photons is defined by the thermal
equilibrium Bose-Einstein statistics at temperature
T
, i.e.,
N =
[exp (2πf/T ) − 1]
−1
. In the following, we will refer as
N
0
(
N
1
) the average number of photons for the mode
ˆa
0
(
ˆa
1
).
The thermal modes
ˆa
0
and
ˆa
1
pass through a beamsplitter, as
shown in Fig. 1. This generates a signal mode
ˆa
(C)
S
and an
idler mode ˆa
(C)
I
, related to the inputs as [22]
ˆa
(C)
S
ˆa
(C)
I
!
=
√
ξ
√
1 − ξe
iϕ
−
√
1 − ξe
−iϕ
√
ξ
ˆa
0
ˆa
1
. (2)
Here,
ξ ∈ (0, 1)
is the reflection coefficient and
ϕ
is the phase
turning angle of the beamsplitter, in the following set to be
zero. One can think of this process as a noise signal, generated
by a thermal source at temperature
T
0
, sent as input of a
power divider placed in an environment at temperature
T
1
.
The output modes
ˆa
(C)
S
and
ˆa
(C)
I
are in a thermal state with
ξN
0
+ (1 − ξ)N
1
and
ξN
1
+ (1 − ξ)N
0
average number of
photons, respectively. If
T
1
6= T
0
, or, equivalently,
N
1
6= N
0
,
then the outputs are classically-correlated, regardless of the
value of ξ.
2) Entangled thermal noise: A Two-Mode Squeezed Vac-
uum (TMSV) state |ψi
TMSV
is represented in the Fock basis
as
|ψi
TMSV
=
∞
X
n=0
s
N
n
S
(N
S
+ 1)
n+1
|ni
S
|ni
I
, (3)
where
N
S
is the average number of photons in both the signal
and idler mode. A TMSV state is closely related to a classically-
correlated thermal noise, as also here both signal and idler
photons are Bose-Einstein distributed. However, as we will see,
the resulting correlations in the low signal-power regime are
stronger for the TSMV states.
1
All variables using the symbol
N
refer to mode quanta and should not be
confused with the noise figure of a microwave component, which often shares
the same symbol.
B. Covariance and correlation matrices
As the states considered here are Gaussian, their statistics
is entirely determined by the first and second order quadrature
moments. For zero-mean states, i.e., when
h
ˆ
X
i
i = 0
for all
i
,
the states are characterized entirely by the covariance matrix
Σ, with elements
Σ
i,j
=
1
2
h
ˆ
X
i
ˆ
X
†
j
+
ˆ
X
j
ˆ
X
†
i
i − h
ˆ
X
i
ih
ˆ
X
†
j
i. (4)
This is the case for both the classical and the entangled
thermal noise states. Similarly, one can introduce the correlation
coefficient matrix R, whose elements are
R
i,j
=
Σ
i,j
p
Σ
i,i
p
Σ
j,j
∈ [−1, 1]. (5)
These coefficients, also referred to as Pearson’s correlation
coefficients, characterize the linear dependence between the
quadratures
ˆ
X
i
and
ˆ
X
j
.
C. Quantum relative entropy
The quantum relative entropy defines an information measure
between two quantum states. It is defined as
D(ρ
1
||ρ
0
) = Tr ρ
1
(ln ρ
1
− ln ρ
0
), (6)
for two density matrices
ρ
0
and
ρ
1
. This quantity is related to
the performance in the asymmetric binary hypothesis testing
via the quantum Stein’s lemma. The task is to discriminate
between
M
copies of
ρ
0
and
M
copies of
ρ
1
, given a bound
on the type-I error probability (probability of false alarm,
P
F a
)
of
ε ∈ (0, 1)
. In this discrimination, the maximum type-II error
probability (probability of miss, P
M
) exponent is
−
ln P
M
M
= D(ρ
1
||ρ
0
) +
r
V (ρ
1
||ρ
0
)
M
Φ
−1
(ε) + O
ln M
M
, (7)
where
V (ρ
1
||ρ
0
) = Tr ρ
1
[ln ρ
1
− ln ρ
0
− D(ρ
1
||ρ
0
)]
2
is the
quantum relative entropy variance and
Φ
−1
is the inverse
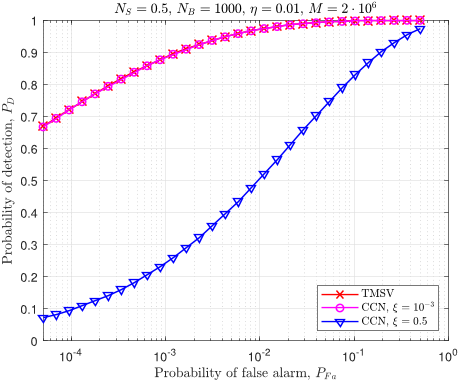
cumulative normal distribution [23]. In this work, we rely on
quantum relative entropy computations and its variance in order
to quantify the performance in the asymptotic setting, i.e., when
M 1
. This is in contrast to the original treatment based on
the Chernoff bound [2], which provides an estimation of the
average error probability when the prior probabilities of target
absence or presence are equal. In a typical radar scenario, the
prior probabilities are not the same, and may be even unknown.
III. NOISE RADAR OPERATION
In this section, we analyze the performance of the classical
and quantum noise correlated radars, based on the states defined
in the previous section.
A. Probing the environment
The signal mode is transmitted to probe the environment
where an object (target) may be present or absent. This process
is modelled as a channel with reflection coefficient
η
that is
non-zero and small when the target is present (
0 < η 1
)
and zero when the target is absent (
η = 0
), see Fig. 2. Here,
η
can be interpreted as the ratio between transmitted power and
Preparation
Detection
ˆa
I
ˆa
S
ˆa
R
ˆa
B
η
Fig. 2.
Scheme of the quantum and classical noise radar systems.
The
system probes a region of space with a signal
ˆa
S
to detect a possible object,
modelled as a channel with reflectivity parameter
η
. The returned signal
ˆa
R
is then used for detecting correlations with the idler mode
ˆa
I
, which has been
retained in the lab.
received power, including the effects of atmospheric attenuation,
the antenna gain and the target radar cross section. We use
a beamsplitter model to take into account the environmental
losses. In other words, the returned mode ˆa
R
is given by
ˆa
R
=
√
η ˆa
S
e
−iθ
+
p
1 − η ˆa
B
, (8)
where
ˆa
B
is a bright background noise mode with
hˆa
†
B
ˆa
B
i =
N
B
average power per mode, and where
θ
is a phase shift
relative to the idler. In the
1 − 10
GHz regime, where the
technology is advanced enough to apply these ideas in the
quantum regime, we have that
N
B
' 10
3
, which is assumed
for numerical computations. For the current calculation, the
reflection coefficient is assumed to be non-fluctuating. We also
assume
hˆa
I
ˆa
B
i = 0
, i.e., the returned signal preserves some
correlations with the idler mode only if the object is present.
This allows us to define a correlation detector able to detect
the presence or absence of the object.
B. Cross-correlation coefficient
The covariance matrix of the system composed of the
received signal and the idler is easily computable using Eq.
(4)
and Eq.
(8)
. For both the classical and the quantum noise radars
considered here, applying Eq.
(5)
gives us the correlation matrix
R =
I κD(θ)
κD(θ)
T
I
, (9)
where
0 ≤ κ ≤ 1
is the amplitude of the cross-correlation
coefficient, and
D
is a matrix with determinant
|D| = ±1
. The
cross-correlation coefficient for the entangled TMSV source
can be derived directly from the definition,
κ
TMSV
=
p
ηN
S
(N
S
+ 1)
q
N
R
+
1
2
q
N
S
+
1
2
, (10)
with
N
R
= ηN
S
+ (1 −η)N
B
. For a fair comparison between
the quantum and classical systems, we introduce a constraint
on the transmitted power of the signal modes, i.e., we set
N
S
= ξN
0
+ (1 − ξ)N
1
. (11)
This constraint can be interpreted as giving both systems equal
LPI properties. Eq.
(11)
yields an expression for the classical
cross-correlation amplitude as
κ
CCN
=
√
η(N
S
− N
1
)
q
N
R
+
1
2
q
N
S
− N
1
+
ξ
1−ξ
N
1
+
1
2
, (12)
where
N
S
> N
1
follows directly from Eq.
(11)
and the
assumption
N
0
> N
1
. This quantity is maximal in the
N
1
1
regime, where Eq.
(11)
reduces to
N
S
= ξN
0
. We assume
N
1
1
, which corresponds to classically-correlated thermal
noise generated in a noise-free environment. At microwave
frequencies this is achievable at mK temperatures. Eq.
(12)
,
for given noise transmitting power, defines the correlations of
a class of classical noise radars, labeled by the beamsplitter
parameter ξ.
C. Quantum advantage
It is easy to see that the quantity
κ
2
is linearly proportional
to the effective SNR in the likelihood-ratio tests. A larger value
of
κ
2
means a stronger discrimination power. Therefore, we
define a figure of merit
Q
A
, quantifying the advantage of the
quantum over the classical noise radar, as
Q
A
≡
κ
2
TMSV
κ
2
CCN
=
N
S
+ 1
N
S
+
1
2
1 +
ξ
2N
S
(1 − ξ)
, (13)
which can be evaluated for different values of the free parameter
ξ
. Restricting the constraint to equal power in both the signal
and idler mode is equivalent to applying a 50-50 beamsplitter
to the thermal noise source in Eq.
(2)
, or, in other words, it
corresponds to setting ξ = 1/2. This gives
Q
A
(ξ = 1/2) = 1 +
1
N
S
, (14)
which is unbounded for
N
S
→ 0
. This setting as been used as
benchmarking in the recent microwave quantum illumination
experiments [12], [13]. However, this choice of
ξ
is not optimal,
leading to an overestimation of the quantum radar advantage
2
.
A strongly asymmetric beamsplitter must be applied to a
very bright noise source (
N
0
1
) in order to maximize
the correlations in the classical case, while maintaining the
constraint on transmitted power
N
S
= ξN
0
. It can be seen in
Eq.
(13)
, that
Q
A
is maximized in the
ξ/(1 − ξ) N
S
limit.
In this setting, the CCN idler has a much better SNR than in
the symmetric configuration, and we get
Q
A
(ξ/(1 − ξ) N
S
) ≈ 2
1 −
N
S
2N
S
+ 1
. (15)
In the low transmitting power limit we have that
lim
N
S
→0
Q
A
= 2
,
i.e., a
√
2
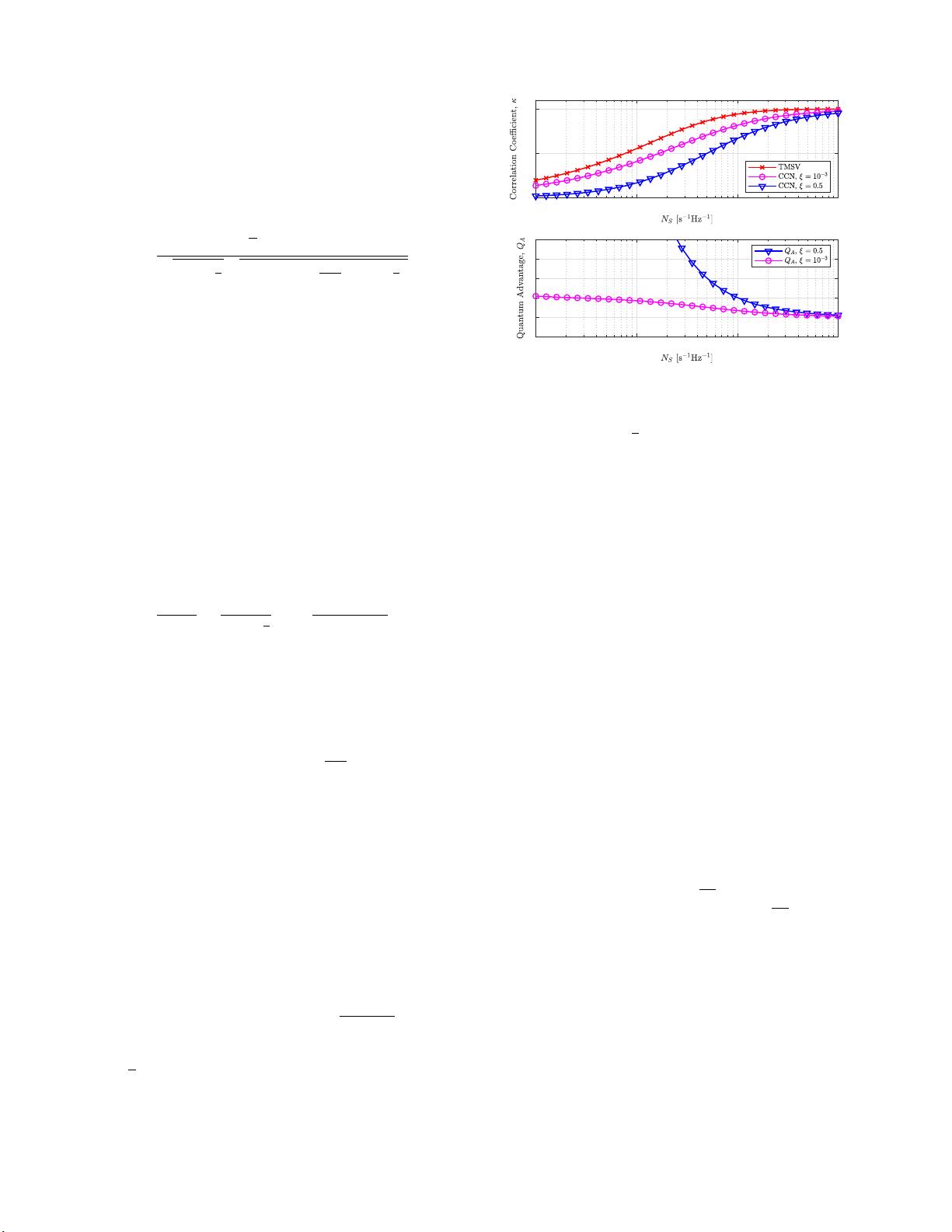
advantage in the correlation coefficient. In Fig. 3 we
2
This criticism was already raised by J. H. Shapiro in Ref. [14].
10
-2
10
-1
10
0
10
1
0
0.5
1
10
-2
10
-1
10
0
10
1
0
1
2
3
4
5
Fig. 3.
Performance of the quantum and classical noise radars in terms
of the cross-correlation coefficient.
(Upper) The cross-correlation coefficients
for the quantum and classical noise radars, as functions of the transmitted
quanta, rescaled such that
√
η = 1
. (Lower) The quantum advantage for the
cases considered above. In both plots, we have considered the
ξ = 10
−3
and
ξ = 0.5
settings. The first setting achieves a close to optimal cross-correlation
coefficient. The second setting is suboptimal, and it has been used as classical
reference in recent microwave illumination experiments [12], [13].
show the functional behaviour of the correlation coefficients for
the entangled and classically-correlated thermal noise source,
depending on the transmitting power
N
S
. The quantum advan-
tage decays slowly with increasing
N
S
, keeping an advantage
also for finite
N
S
, until virtually disappearing for
N
S
' 10
.
Note that in the limit where the advantage is maximized, the
modes also become uncorrelated (
κ → 0
) in both systems. A
signal-idler system with a large operating bandwidth is needed
to compensate the low amount of correlations per mode in the
N
S
1 limit.
Here, the phase-shift of the signal mode due to the prop-
agating path has been set to zero. In other words, we work
in a rotated frame, where the inter-mode phase angle
θ
is
applied only to the idler mode, i.e.,
ˆa
I
7→ ˆa
I
e
−iθ
. Note that,
in general, the phase
θ
is unknown. The original QI protocol
assumes the knowledge of the inter-mode phase angle
θ
. In
this case, the complex conjugate receiver defined in Ref. [24]
saturates the quantum advantage given in Eq.
(13)
with a
likelihood-ratio test [25]. If
θ
is unknown, then one can define
an adaptive strategy where
O(
√
M)
copies are used to get
a rough estimate of
θ
, and then
M − O(
√
M)
are used to
perform the discrimination protocol in the optimal reference
frame maximizing the Fisher information [7]. This strategy
shows the same asymptotic performance as in the case of
known θ.
D. The effect of amplification
In the following, we consider three Gaussian amplifying
schemes. We show how the quantum advantage defined in
terms the cross-correlation coefficients rapidly disappears when
an amplification is involved at any stage of the protocol.