This is a repository copy of 3D SPH simulation of dynamic water surface and its
interaction with underlying flow structure for turbulent open channel flows over rough beds.
White Rose Research Online URL for this paper:
http://eprints.whiterose.ac.uk/141894/
Version: Accepted Version
Article:
Gabreil, E.O., Tait, S., Nichols, A. et al. (1 more author) (2019) 3D SPH simulation of
dynamic water surface and its interaction with underlying flow structure for turbulent open
channel flows over rough beds. International Journal of Ocean and Coastal Engineering, 1
(2). 1840003. ISSN 2529-8070
https://doi.org/10.1142/S2529807018400031
Electronic version of an article published as International Journal of Ocean and Coastal
Engineering, Vol. 01, No. 02, 1840003 (2018) https://doi.org/10.1142/S2529807018400031
© copyright World Scientific Publishing Company
https://www.worldscientific.com/worldscinet/ijoce
eprints@whiterose.ac.uk
https://eprints.whiterose.ac.uk/
Reuse
Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless
indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by
national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of
the full text version. This is indicated by the licence information on the White Rose Research Online record
for the item.
Takedown
If you consider content in White Rose Research Online to be in breach of UK law, please notify us by
emailing eprints@whiterose.ac.uk including the URL of the record and the reason for the withdrawal request.

1
3D SPH Simulation of Dynamic Water Surface and its Interaction with Underlying Flow
Structure for Turbulent Open Channel Flows over Rough Beds
Eslam Gabreil, Lecturer in Water Engineering, Department of Civil Engineering, Al-Jabal Al-Gharbi University,
Gharian, Libya, Email: eslamgabreil@yahoo.com
Simon Tait, Professor of Water Engineering, Department of Civil Engineering, University of Sheffield, Sheffield
S1 3JD, UK, Email:
s.tait@sheffield.ac.uk
Andrew Nichols, Lecturer in Water Engineering, Department of Civil and Structural Engineering, University of
Sheffield, Sheffield S1 3JD, UK, Email: a.nichols@sheffield.ac.uk
Giulio Dolcetti, Research Associate, Department of Civil and Structural Engineering, University of
Sheffield, Sheffield S1 3JD, UK, Email. g.dolcetti@sheffield.ac.uk
Abstract
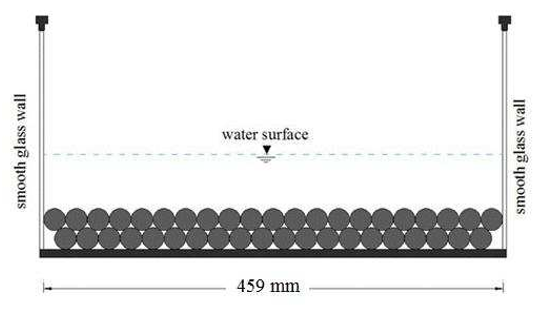
In this study a fully 3D numerical model based on the Smoothed Particle Hydrodynamics
(SPH) approach has been developed to simulate turbulent open channel flows over a fixed
rough bed. The model focuses on the study of dynamic free surface behaviour as well as its
interaction with underlying flow structures near the rough bed. The model is improved from
the open source code SPHysics (http://www.sphysics.org) by adding more advanced
turbulence and rough bed treatment schemes. A modified sub-particle-scale (SPS) eddy
viscosity model is proposed to reflect the turbulence transfer mechanisms and a modified drag
force equation is included into the momentum equations to account for the existence of
roughness elements on the bed as well as on the sidewalls. The computed results of
variousfree surface patterns have been compared with the laboratory measurements of the
fluctuating water surface elevations in the streamwise and spanwise directions of a
rectangular open channel flow under a range of flow conditions. The comparison has
demonstrated that the proposed 3D SPH model can simulate well the complex free surface
flows over a fixed rough bed.
Keywords: SPHysics; free surface flow; rough bed; flow surface dynamics; underlying flow
structure; flow turbulence; bed drag

2
1. Literature Review on Dynamic Water Surface Patterns in Turbulent Open
Channel Flow
Flows with a free surface in civil engineering applications are mainly turbulent. These include
flows in man-made channels and rivers. The study of turbulent flow structures for flows with
a free surface is essential to understanding the fluid dynamics for such civil engineering
applications. All turbulent flow structures in the natural environment are inherently three-
dimensional (3D). These types of flow are characterised by turbulent structures at a range of
scales, intense energy dissipation, and random vorticity [Mathieu and Scot, 2000].
When a fluid flows over a solid boundary, the fluid-air interface is often observed to be
wrinkled. In open channel flows with the absence of the wind, the vertical velocities must
dissipate at the surface, generating horizontal velocities and deforming the surface.
Furthermore, turbulent eddies can never die inside the flow; they must end perpendicularly at
the free surface, causing temporal changes in water surface elevation above these vortices
[Smolentsev and Miraghaie, 2005; Savelsberg and Van de Water, 2009]. Studies of the
dynamic behaviour of water surfaces requires the measurement of the instantaneous
elevations of the water surface and the instantaneous velocities of the underlying flow.
Several techniques have been used to provide a means of measuring these instantaneously and
synchronously [Dabiri, 2003; Savelsberg and Van de Water, 2006; Cooper et al, 2006;
Nichols et al, 2010; Nichols et al, 2016]. Horoshenkov et al. [2013] measured the
instantaneous water surface elevations in turbulent open channel flows using conductance
wave probes. The advantage of using conductance wave probes is that, they are easy to set up
and calibrate compared to the early mentioned techniques. Conductance wave probes can also
be operated at different frequencies to avoid mutual interaction between two or more closely
spaced probes, and generally provide high dynamic accuracy.
A number of experimental studies have been conducted and reported in the literature on
understanding the linkage between the dynamic behaviour of the water surface and the
turbulent flow structures underneath it [e.g., Smolentsev&Miraghaie, 2005; Cooper at al.,
2006; Savelsberg et al., 2006; Savelsberg & Van de Water, 2009; Fujita et al., 2011;
Horoshenkov et al., 2013; Krynkin et al., 2014]. Kumar et al. [1998] performed an
experimental investigation of the characteristics of free surface turbulence in horizontal glass
channel flow with Reynolds Numbers ranging from 2800 to 8800. Their results indicated that
the persistent structure of the water-air interface can be classified into three types: upwellings,
downwellings and spiral eddies. Statistical analyses of Dabiri [2003] have shown that the free
surface deformation is strongly correlated with the near surface vorticity field with a
correlation coefficient of about 0.7 to 0.8. Smolentsev and Miraghaie [2005] performed an
experimental study of flow conditions ranging from weak to strong turbulence in very wide
open channel having an aspect ratio (flow width/flow depth) higher than 40. They observed
that three types of disturbance are always presented on the free surface at the same time:
capillary waves, gravity waves and turbulent waves that are generated due to the interactions
between the bulk flow and the water surface. The turbulent waves were found by [Smolentsev

3
and Miraghaie, 2005] to be the most dominant type, having a characteristic size (in the free
surface plane)of approximately half the mean flow depth. An interesting feature has also been
observed on the free surface is that these turbulent waves have celerity very close to the
average flow velocity, while the speed of capillary and gravity waves were different. This
feature was also observed by Fujita et al. [2011]and Nicholas [2014] who stated that the water
surface waves travel with velocity close to the mean flow velocity. Savelsberg and Van de
Water [2009] reported that although there are several appealing relations between subsurface
flow field and water surface gradient, the water surface of fully developed turbulent flow
exhibits a dynamic behaviour of its own. They attributed this to the large eddies of subsurface
turbulent flow exciting random gravity and capillary waves which move in all directions
across the water surface. Fujita et al. [2011] showed that there is a correlation between the
vertical velocity components and the boil vortices on the surface that are not due to the
gravity waves. Horoshenkov et al. [2013] experimentally studied the free surface dynamic
behaviour and its interactions with the underlying turbulence of shallow open channel flows
over a gravel bed. The temporal change in water surface elevations was measured using
conductance wave probes in the centre of the channel at different streamwise positions. They
found that the free surface roughness patterns are strongly controlled by bulk flow properties
and are not strongly influenced by gravity waves. Horoshenkov et al. [2013] also showed that
the free surface roughness patterns can be described by a well-correlated analytical formula
and established a number of empirical relationships between the water surface parameters and
the corresponding hydraulic parameters. Nichols et al. [2016] determined the free surface
profile for several flow conditions by using the LIF technique and showed that the
independent surface behaviour noted by [Savelsberg and Van de Water, 2009] was not due to
travelling waves, but due to each individual water surface feature oscillating vertically in time
as it is carried in space by the bulk flow. It was concluded that this complex behaviour of
oscillating surface features, overlapping and out of phase in space and time, is responsible for
decorrelating the surface pattern from the turbulence field that generates it. The spatial period
of the oscillation was shown to match the characteristic spatial period of the spatial
correlation functions of [Horoshenkov et al., 2013], giving a physical explanation for the
oscillatory form of spatial correlation function observed.
2. Literature Review on SPH Applications in Open Channel Flows
Numerical simulations are used as a very valuable tool in the field of hydrodynamics and
hydraulic engineering to solve complex problems that are impractical to examine
experimentally. They also have the advantage of disclosing details of flow structures without
the spatial-temporal limitations of laboratory instruments. Thus they can provide an
economical and flexible tool to study flows of practical interest. In numerical simulations, the
physical governing equations are described by one of two main approaches. The first one is
the mesh-based approach in which the fluid domain is decomposed into a fixed grid.
Examples of this approach are Finite Volume (FV), Finite element (FE) and Finite difference
(FD). However, simulating complex flows with large deformations is limited and difficult
with these methods due to the numerical diffusions raised from the advection terms in the
Navier-Stokes (N-S) equations [Gotoh and Sakai, 1999]. The second approach is mesh-free,
where the fluid domain is decomposed into moving points of space commonly called

4
“particles”. The Finite Points [Onate et al., 1996], Free Mesh [Yagawa and Yamada, 1996],
and Moving Particle Semi-implicit (MPS) [Koshizuka et al., 1998] techniques are all
examples of mesh-free approaches. Such techniques are inherently well suited for the
simulation of flows with complex boundaries. In recent years, the most popular Lagrangian
mesh-free method to have been used is Smoothed Particle Hydrodynamics (SPH). Although
the SPH method has been widely used in coastal hydrodynamics, using this method for the
simulation of open channel flow problems has received little attention, especially for the
simulation of turbulent free surface flows over rough beds. The SPH technique, originally
formulated by [Gingold and Monaghan, 1977], initially focussed on the provision of solutions
to astrophysics problems related to the formation and eventual evolution of galaxies [Li and
Liu, 2004]. It finds wide use in solving applied mechanics problems due to its advantage of
using a discretization method to approximate a continuum as a set of particles. The most
compelling advantage of the application of the SPH method is its inherent ability to use the
set of particles to predict the behaviour of highly strained motions without the need for grids
or meshes [Violeau, 2012]. Due to its meshless nature, SPH can handle complex solid
boundaries and can also define free surface flows without the typical problems of grid-based
methods that they need to be coupled with a suitable technique such as volume of fluid (VOF)
to capture the air-water interface.
The treatment of inflow and outflow boundaries in SPH is the key for the successful
simulation of open channel flow problems. In recent years, different inflow and outflow
boundaries have been implemented. For example, Lee et al. [2008] used a periodic open
boundary by which the fluid particles that leave the computational domain through the
outflow boundary are instantly re-inserted at the inflow boundary, and the fluid particles close
to one open lateral boundary interact with the fluid particles close to the complementary open
lateral boundary on the other side of the computational domain. However, this boundary
treatment is not suitable for applications in which the fluid volume leaving the computational
domain does not have the same fluid volume that needs to be generated to enter the
computational domain at the same time. In the technique developed by Shakibaeinia and Jin
[2010], the fluid particles leaving and entering the computational domain are added to and
subtracted from an additional type of particles called ’storage particles’ which exist before the
inlet and after the outlet of the domain of interest. With the method used by Federico et al.
[2012], the desired pressure and velocity conditions are imposed at the inflow region to the
inflow particles and water depth time series are determined by increasing or decreasing the
number of particles in the vertical direction. Meister et al. [2014] performed the same
numerical technique and the analytical solution of the main velocity and the corresponding
pressure distribution were initially imposed. Moreover, Tan et al. [2015] performed an
incompressible SPH (ISPH) technique to simulate open channel turbulent flows over a
smooth bed. The comparisons indicated that the velocity trend in the upper region is quite
promising, but the error becomes larger near the channel bed as the flow depth becomes
shallower. Kazemi et al. [2017] used similar techniques of Federico et al. [2012] and Tan et al.
[2015], but with the difference in that the inflow particle velocities are linked with those of
the inner fluid particles, so that the flow is evolved naturally without any prescription of the
inflow velocity.