scispace - formally typeset
Journal Article•DOI•

Coverage Probability and Achievable Rate Analysis of FFR-Aided Multi-User OFDM-Based MIMO and SIMO Systems

Suman Kumar1, Sheetal Kalyani1, Lajos Hanzo2, Krishnamurthy Giridhar1 •
Indian Institute of Technology Madras1, University of Southampton2
07 Aug 2015-IEEE Transactions on Communications (IEEE)-Vol. 63, Iss: 10, pp 3869-3881

...read more

Content maybe subject to copyright    Report

IEEE
Proof
IEEE TRANSACTIONS ON COMMUNICATIONS 1
Coverage Probability and Achievable Rate Analysis
of FFR-Aided Multi-User OFDM-Based
MIMO and SIMO Systems
1
2
3
Suman Kumar, Sheetal Kalyani, Lajos Hanzo, Fellow, IEEE, and K. Giridhar, Member, IEEE4
Abstract—Expressions are derived for the coverage probability5
and average rate of both multi-user multiple input multiple output6
(MU-MIMO) and single input multiple output (SIMO) systems7
in the context of a fractional frequency reuse (FFR) scheme. In8
particular, given a reuse region of
1
3
(FR3) and a reuse region of9
1 (FR1) as well as a signal-to-interference-plus-noise-ratio (SINR)10
threshold S
th
, which decides the user assignment to either the FR111
or FR3 regions, we theoretically show that: 1) the optimal choice12
of S
th
which maximizes the coverage probability is S
th
= T,where13
T is the target SINR required for ensuring adequate coverage, and14
2) the optimal choice of S
th
which maximizes the average rate is15
given by S
th
= T
,whereT
is a function of the path loss exponent,16
the number of antennas and of the fading parameters. The impact17
of frequency domain correlation amongst the OFDM sub-bands18
allocated to the FR1 and FR3 cell-regions is analysed and it is19
shown that the presence of correlation reduces both the coverage20
probability and the average throughput of the FFR network.21
Furthermore, the performance of our FFR-aided MU-MIMO and22
SIMO systems is compared. Our analysis shows that the (2 × 2)23
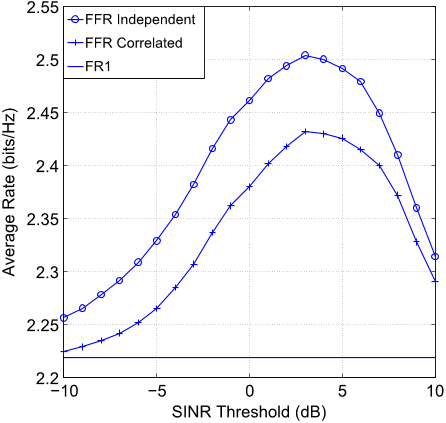
MU-MIMO system achieves 22.5% higher rate than the (1 × 3)24
SIMO system and for lower target SINRs, the coverage probability25
of a (2 × 2) MU-MIMO system is comparable to a (1 × 3) SIMO26
system. Hence the f ormer one may be preferred over the latter.27
Our simulation results closely match the analytical results.28
Index Terms—Author, please supply index terms/keywords for29
your paper. To download the IEEE Taxonomy go to http://www.30
ieee.org/documents/taxonomy_v101.pdf.31
I. INTRODUCTION32
O
RTHOGONAL frequency division multiple access
AQ1
33
(OFDMA) based systems maintain orthogonality among34
the intra-cell users, but the radical OFDMA system deploy-35
ments relying on a frequency reuse factor of unity suffer from36
inter-cell interference. As a remedy, inter-cell interference coor-37
dination (ICIC) schemes have been designed for minimizing the38
co-channel interference [1]. Fractional frequency reuse (FFR)39
[2] constitutes a low complexity ICIC scheme, which has been40
proposed for OFDMA based wireless networks such as IEEE41
WiMAX [3] and 3GPP LTE [4].42
Manuscript received January 18, 2015; revised June 5, 2015; accepted
August 1, 2015. The associate editor coordinating the re view of this paper and
approving it for publication was O. Oyman.
S. Kumar, S. Kalyani, and K. Giridhar are with the Indian Institute of
Technology Madras, Chennai 600 036, India (e-mail: ee10d040@ee.iitm.ac.in;
AQ2
skalyani@ee.iitm.ac.in; giri@ee.iitm.ac.in).
L. Hanzo is with the School of Electrical and Computer Science, University
of Southampton, Southampton SO17 1BJ, U.K. (e-mail: lh@ecs.soton.ac.uk).
Color versions of one or more of the figures in this paper are available online
at http://ieeexplore.ieee.org.
Digital Object Identifier 10.1109/TCOMM.2015.2465907
Fig. 1. Frequency allocation in FFR for three neighbouring cells with δ = 3.
The cell-centre users of all the cells rely on a common frequency band F
0
, while
the cell-edge users of the three cells occupy different frequency bands, namely
F
1
, F
2
and F
3
.
Explicitly, FFR is a combination of frequency reuse 1 (FR1) 43
and frequency reuse
1
δ
(FRδ). FR1 allocates all the frequencies 44
to each cell, leading to a unity spatial reuse, hence results in 45
a low-quality coverage due to the excessive inter-cell interfer- 46
ence. On the other hand, FRδ allocates a fraction of
1
δ
of the 47
frequencies to each cell and therefore reduces the area-spectral- 48
efficiency, but improves the SINR. FFR strikes an attractive 49
trade-off by exploiting the advantages of both FR1 and FRδ by 50
relying on FR1 for the cell-centre users i.e. for those users who 51
would experience less interference from the other cells, because 52
they are close to their serving base station (BS). By contrast, 53
FRδ is invoked for the cell-edge users i.e. for those users who 54
would experience high interference afflicted by the co-channel 55
signals emanating from the neighbouring cells in case of FR1, 56
because they are far from their serving BS. Typically, there 57
are two basic modes of FFR deployment: static and dynamic 58
FFR [1]. In this paper, we consider the more practical static 59
FFR scheme, where all the parameters are configured and kept 60
fixed over a certain period of time [5]. Fig. 1 depicts a typical 61
frequency allocation in the context of the FFR scheme for three 62
adjacent cells, where F
1
, F
2
and F
3
each use x% of the total 63
spectrum, hence F
0
uses (100 − 3x)% of the spectrum. 64
FFR schemes have been lavishly studied using both system 65
level simulations and theoretical analysis [6]–[11]. The optimiz- 66
ation of FFR relying on a distance threshold
1
or SINR threshold
2
67
1
Based on a pre-determined distance from the BS, the subscribers are divided
into cell-centre as well as cell-edge users and hence here the design parameter
is a distance threshold (R
th
).
2
Based on a pre-determined SINR, the subscribers are divided into cell-
centre as well as cell-edge users and here the design parameter is the SINR
threshold (S
th
).
0090-6778 © 2015 IEEE. Personal use is permitted, but republication/redistribution requires IEEE permission.
See http://www.ieee.org/publications_standards/publications/rights/index.html for more information.
IEEE
Proof
2 IEEE TRANSACTIONS ON COMM UNICATIONS
has been studied using graph theory in [6] and convex optimiza-68
tion in [7]. Specifically, it h as been shown in [7] that the optimal69
frequency reuse factor is FR3 for the cell-edge users. The av-70
erage cell throughput of an FFR system was derived in [8] as a71
function of the distance threshold. It was shown in [9] that there72
exists an optimal radius threshold for which the average rate be-73
comes maximum. The performance of FFR and soft frequency74
reuse (SFR) has been studied in [12] under both fully loaded75
and partially loaded scenarios. An algorithm was proposed76
in [13] for enhancing the network capacity and the cell-edge77
performance for a dynamic SFR deployment relying on re-78
alistic irregularly shaped cells. A fuzzy logic based generic79
model was proposed for deriving different frequency reuse80
schemes in [14]. As a further development, an FFR based 3-cell81
network-MIMO based tri-sector BS architecture was presented82
in [15]. FFR and SFR are compared in the presence of corre-83
lated interferers in [16]. The optimal configuration o f FFR is84
determined in [17] for a high-density wireless cellular network.85
The authors of [18] have proposed a distributed and adaptive86
solution for interference coordination based on the center of87
gravity of users in each sector. An optimal FFR and power88
control scheme which can coordinate the interference among89
the heterogeneous nodes is proposed in [19].90
An analytical framework of calculating both the coverage91
probability (CP
r
) and the average rate of FFR schemes was92
presented in [10] and [11] for homogeneous single input single93
output (SISO) and MIMO heterogeneous networks, respec-94
tively, using a Poisson point process (PPP). However, the au-95
thors of [10], [11] assumed having an unplanned FFR network,96
where the cells using the same frequency set are randomly97
allocated. Hence, two cells using the same frequency for the98
cell-edge users may in fact be co-located [10], [11]. However,99
in case of FFR based deployments the regions using the same100
frequency are typically planned to be as far apart as possible101
and our focus is on these types of deployments. An FFR-aided102
distributed antenna system (DAS) and an FFR-aided picocell103
was studied in [20] and [21]. While, an FFR-aided femtocell104
has been extensively studied in [22]–[26].105
However, most of the work based on FFR has considered the106
conventional SISO case. To the best of our knowledge, no prior107
work has analytically derived the optimal SINR threshold for108
FFR, when the number of antennas is high at the transmitter109
and/or at the receiver. Hence, in this work, we derive both the110
CP
r
and the average achievable rate expressions of FFR in the111
presence of both MU-MIMO as well as of SIMO systems and112
derive the optimal SINR threshold corresponding to the desired113
CP
r
and throughput. Furthermore, the performance of FFR-114
aided MU-MIMOs is compared to that of FFR in the presence115
of a SIMO system.116
The key benefit of MU-MIMO is their ab ility to improve117
the spectral efficiency, which has b een extensively studied in118
a single-cell context in the presence of AWGN [27]–[29].119
However, it has been shown in [30], [31] with the h elp of120
simulation, that the efficiency of MU-MIMOs is significan tly121
eroded in a multi-cell environment due to interference, es-122
pecially in the cell-edge region. FFR is capable of signifi-123
cantly improving the cell-edge coverage since it uses FR3 for124
the cell-edge users. Hence we study FFR-aided MU-MIMOs125
and quantify their average throughput as well as coverage 126
probability. 127
Furthermore, we carefully examine the correlation of the sub- 128
bands F
0
, F
1
, F
2
and F
3
in Fig. 1 used in the FFR system 129
considered. All prior work on FFR has assumed that the sub- 130
bands experience independent fading, which is mathematically 131
convenient, but practically not realisable. Indeed, when we 132
consider practical transmission block based modulation such as 133
OFDM, the channel’s delay spread is assumed to b e confined to 134
the cyclic prefix of the OFDM symbol. Such a limited-duration 135
(typically less than 20% of the useful OFDM symbol duration) 136
impulse response will result in correlation amongst the adjacent 137
freque ncy domain OFDM sub-channels. More explicitly, unless 138
the sub-bands F
0
···F
3
are spaced apart by more than the recip- 139
rocal of the delay spread, correlation will exist. Since the delay 140
spread experienced in the downlink is user-dependent, it is vir- 141
tually impossible to ensure that the sub-bands F
i
in Fig. 1 are in- 142
dependent for each user scheduled in the downlink. Therefore, 143
in our analysis we will specifically take into account the corre- 144
lation of the sub-bands. For FFR-aided MU-MIMO and SIMO 145
systems, the expressions of CP
r
and average rate are derived 146
and the following new results are presented: 147
(a) The optimal SINR threshold that m aximizes th e CP
r
of 148
FFR is derived for a given T. We show that the optimal 149
S
th
(denoted by S
opt,C
)isS
th
= T for both the MU-MIMO 150
and SIMO system, and if we choose the SINR threshold 151
to be S
opt,C
, then the achievable CP
r
of FFR is higher 152
than that of FR3. The improvement of the FFR CP
r
over 153
that of FR3 is due to the resultant sub-band diversity gain 154
achieved by the systems when a user is classified as either 155
a cell-centre or a cell-edge user. 156
(b) The optimal SINR threshold that maximizes the average 157
rate of FFR is derived. We show that the optimal S
th
(de- 158
noted by S
opt,R
) is equal to T
for both MU-MIMO and 159
SIMO systems, where T
is a fixed SINR value, which de- 160
pends on the system p arameters such as the path loss expo- 161
nent, the number of antennas, the fading parameters, etc. 162
(c) The correlation of the sub-bands always degrades both the 163
CP
r
and the average rate of the FFR-aided MU-MIMO 164
and SIMO systems. 165
(d) The performance of FFR-aided MU-MIMO and SIMO 166
systems is compared. It is shown that system designer 167
may choose the (2 × 2) MU-MIMO system over (1 × 3) 168
SIMO system of FFR scheme as MU-MIMO achieves 169
significant gain in average rate over SIMO. 170
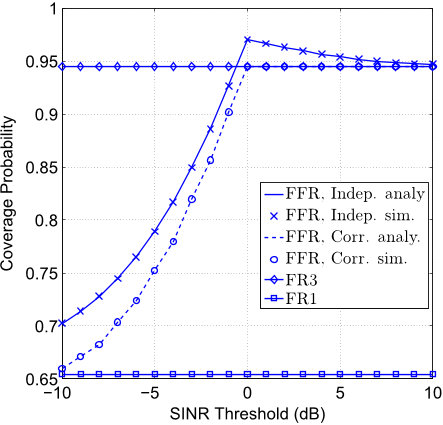
We will demonstrate that our analytical results are in close 171
agreement with the simulation results. Moreover, it is shown 172
that at optimal S
th
, the FFR achieves significantly high gain in 173
CP
r
than that of average rate with respect to FR1 and hence this 174
scheme would be more useful when coverage gain is essentially 175
required. Therefore, FFR-aided MU-MIMO provides both high 176
average rate and satisfactory CP
r
foralowervalueofN
a
. 177
II. SYSTEM MODEL 178
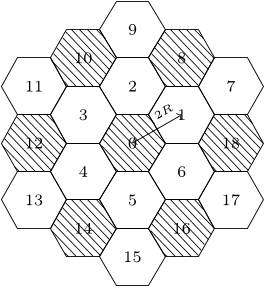
A homogeneous macrocell network relying on hexagonal 179
tessellation and on an inter cell site distance of 2R is considered, 180
IEEE
Proof
KUMAR et al.: COVER AGE PROBABILITY AND ACHIEVABLE RATE ANALYSIS OF MU-MIMO AND SIMO SYSTEMS 3
Fig. 2. Hexagonal structure of 2-tier macrocell. Interference for 0th cell in
FR1 system is contributed form all the neighbouring 18 cells, while in a FR3
system it is contributed only from the shaded cells.
as shown in Fig. 2. Both a MU-MIMO and a SIMO system is181
considered. We assume that in the MU-MIMO case each user182
is equipped with N
r
receive antennas, while the BS is equipped183
with N
t
transmit antennas and that N
t
= N
r
. Our focus is on the184
downlink and hence N
t
transmit antennas are used for transmis-185
sion, while the N
r
receive antennas at the UE are u sed for re-186
ception. We also assume that all N
t
transmit antennas at the BS187
are u tilized to transmit N
t
independent data steams to its own N
t
188
users. A linear minimum mean-square-error (LMMSE) receiver189
[32] is considered. In order to calculate the p ost-processing190
SINR of this LMMSE r eceiver, it is assumed that the (N
r
− 1)191
closest interferers can be completely cancelled using the anten-192
nas at the receiver.
3
For example, in the MU-MIMO case, the193
user will not experience any intra-tier interference emanating194
from the serving BS as N
t
= N
r
. In the SIMO case each user195
is equipped with N
r
antennas. The SINR η
t
(r) of a user in the196
MU-MIMO system and the SINR η
r
(r) of a user in the SIMO197
system located at r meters from its serving BS are given by198
η
t
(r) =
gr
−α
σ
2
P
+ I
t
, I
t
=
i∈ψ
N
t
j=1
h
ij
d
−α
i
(1)
and
199
η
r
(r) =
gr
−α
σ
2
P
+ I
r
, I
r
=
i∈ψ
r
h
ij
d
−α
i
, (2)
respectively, where the transmit power of a BS is denoted by P.
200
Here ψ is the set of interfering BSs in the FR1 network and ψ
r
201
denotes all the interfering BSs, excluding the nearest (N
r
− 1)202
interferers, while N
t
denotes the number of transmit antennas.203
The standard path loss model of x
−α
is assumed, where204
α ≥ 2 is the path loss exponent and x is the distance of a user205
from the BS. We assumed that the users are at least at a distance206
of d away from the BS.
4
The noise power is d enoted by σ
2
.207
Here, r and d
i
are the distances from the user to the serving BS208
andtothei
th
interfering BS, respectively, while g and h
i
denote209
3
It is widely exploited that using the LMMSE receiver (N
r
− 1) interferers
can be mitigated, where N
r
is the number of receive antennas [32]. Ho wever,
for simplicity, we assume that the N
r
− 1 closest interferers can be completely
cancelled.
4
Typically , the path loss model is assumed to be max{d, x}
−α
.
the corresponding channel fading power, which are independent 210
and identically exponentially distributed (i.i.d.) with a unit 211
mean, i.e., g ∼ exp(1) and h
i
∼ exp(1)∀ i. In MU-MIMO case, 212
h
ij
is the channel’s fading power from the j
th
antenna of the 213
i
th
interfering BS to the user and it is i.i.d. with a unit mean. 214
Without loss of generality we have considered a user in the 0
th
215
cell of Fig. 2 in our analysis. 216
Similar to [10], the subscribers are classified as cell-centre 217
users and cell-edge users based on the SINR at the mobile sta- 218
tion. If the calculated SINR of a user is lower than the specified 219
SINR threshold S
th
, the user is classified as a cell-edge user. 220
Otherwise, the user is classified as a cell-centre user. Typically, 221
FFR divides the whole frequency band into a total of (1 + δ) 222
parts, where F
0
is allocated to all the cells for the cell-centre 223
users, as seen in Fig. 1. One of the {1 , ··· ,δ} parts is assigned 224
to the cell-edge users in each cell in a planned fashion. The 225
users are assumed to be uniformly distributed in a cell and all r e- 226
source blocks are uniformly shared among the users. The trans- 227
mit power is assumed to b e fixed. If we have η
t
(r)(or η
r
(r)) ≥ 228
S
th
for a user, then the user will continue to experience the same 229
fading power, i.e., g and h
i
from the user to the serving BS 230
andtothei
th
interfering BS, respectively. However, if we have 231
η
t
(r)(or η
r
(r)) < S
th
for a user, the user is allocated another 232
sub-band (from the set of sub-bands assigned to cell-edge users) 233
and it experiences a new fading power, i.e., ˆg and
ˆ
h
i
from the 234
user to the serving BS and to the i
th
interfering BS, respectively. 235
Based on the coherence bandwidth of the OFDM system, and 236
the bands associated with F
0
to F
3
in Fig. 1 is is possible that ˆg 237
and
ˆ
h
i
are either correlated with or independent of g and h
i
,re-238
spectively. Note that g, ˆg, h
i
,and
ˆ
h
i
are the channel gains in the 239
frequency domain and the term correlation is used for referring 240
to frequency domain correlation in this paper. The correlation 241
depends both on the particular user’s channel conditions and 242
on the instantaneous coherence bandwidth with respect to the 243
FFR frequency bands. To better understand the impact of corre- 244
lation among the sub-bands on the FFR system’s performance, 245
in this paper, we consider the following two extreme cases: 246
Case 1: g and ˆg are independent and also h
i
as well as
ˆ
h
i
,are247
independent for all i. 248
Case 2: g and ˆg are fully correlated and also h
i
as well as
ˆ
h
i
, 249
are fully correlated for all i. 250
In reality these channel output powers may be partially corre- 251
lated, but the analysis of partial (arbitrary) corr e lation is quite 252
complicated and hence it is beyond the scope of this work. 253
However, the analysis of the above two extreme cases we be- 254
lieve, is sufficient for understanding the impact of correlation 255
among the sub-bands. 256
III. COVERAGE PROBABILITY ANA LY S I S O F FFR 257
In this section, we first derive the CP
r
of both the 258
MU-MIMO and SIMO system considered, which is defined 259
as the probability that a randomly chosen user’s instantaneous 260
SINR η
t
(r) is higher than T. This defines, the average fraction 261
of users are having an SINR higher than the target SINR. The 262
coverage prob ability is determined by the complementry cumu- 263
lative distribution function of the SINR over the network. The 264
IEEE
Proof
4 IEEE TRANSACTIONS ON COMM UNICATIONS
CP
r
of a user who is at a distanc e of r meters from the BS in a265
FR1-aided MU-MIMO scenario is given by266
P
1
(T, r) = P [η
t
(r)>T] = P
g > Tr
α
I
t
+ Tr
α
σ
2
P
, (3)
where I
t
is defined in (2). Since g ∼ exp(1), h
ij
∼ exp(1),and267
h
ij
are i.i.d., P
1
(T, r) is given by268
P
1
(T, r) = E
h
ij
e
−Tr
α
I
t
−Tr
α
σ
2
P
=
i∈ψ
N
t
j=1
E
h
ij
e
−Tr
α
h
ij
d
−α
i
× e
−Tr
α
σ
2
P
=
i∈ψ
1
1 + Tr
α
d
−α
i
N
t
e
−Tr
α
σ
2
P
, (4)
where ψ is the set of interfering BSs in a FR1 network.
269
Similarly, the CP
r
of a user located at a distance of r meters270
from the BS in a FR3 network can be formulated as271
P
3
(T, r) =
i∈φ
1
1 + Tr
α
d
−α
i
N
t
e
−Tr
α
σ
2
P
(5)
where φ is the set of interfering cells in the FR3 scheme, w hich
272
is a function of the frequency reuse plan. Also, the CP
r
of a user273
in the SIMO-based FR1 network and in a FR3 network can be274
expressed as275
P
1
(T, r) =
i∈ψ
r
1
1 + Tr
α
d
−α
i
e
−Tr
α
σ
2
P
and
P
3
(T, r) =
i∈φ
r
1
1 + Tr
α
d
−α
i
e
−Tr
α
σ
2
P
. (6)
Here φ
r
denotes the set of interfering cells in the FR3 scheme276
excluding the nearest (N
r
− 1) interferers. Let us now derive277
the CP
r
of FFR for both the independent and correlated cases.278
A. Case 1: g and ˆg are Independent as Well as h
i
and
ˆ
h
i
are279
Also Independent for all i280
The CP
r
P
F,c
(r) of a cell-centre user who is at a distance of281
r meters from the 0
th
BS in a FFR-aided MU-MIMO scenario282
is given by283
P
F,c
(r)
(a)
= P [η
t
(r)>T|η
t
(r)>S
th
]
= P
gr
−α
I
t
+
σ
2
P
> T
gr
−α
I
t
+
σ
2
P
> S
th
,
where (a) follows from the fact that a cell-centre user has SINR
284
≥ S
th
. Upon applying Bayes’ rule, one can rewrite P
F,c
(r) as285
P
F,c
(r) =
P
gr
−α
I
t
+
σ
2
P
> T,
gr
−α
I
t
+
σ
2
P
> S
th
P
gr
−α
I
t
+
σ
2
P
> S
th
=
i∈ψ
1
1+max{T,S
th
}r
α
d
−α
i
N
t
e
− max{T,S
th
}r
α
σ
2
P
j∈ψ
1
1+S
th
r
α
d
−α
j
N
t
e
−S
th
r
α
σ
2
P
. (7)
Similarly, the CP
r
of a cell-edge user who is at a distance of r 286
meters from the BS in the FFR-aided MU-MIMO case P
F,e
(r) 287
is given by 288
P
F,e
(r) = P
ˆη
t
(r)>T|η
t
(r)<S
th
=
P
ˆgr
−α
ˆ
I
t
+
σ
2
P
> T,
gr
−α
I
t
+
σ
2
P
< S
th
P
gr
−α
I
t
+
σ
2
P
< S
th
.
Here, the cell-edge user will experien ce the new interference
289
term of
ˆ
I
t
=
i∈φ
N
t
j=1
ˆ
h
ij
d
−α
i
and the new channel power ˆg,i.e.a290
new SINR ˆη(r) due to the fact that th e cell-edge user is now a 291
FR3 user. Basically, ˆη(r) denotes the SINR experienced by the 292
user at a distance of r meters from the BS in a FR3 system and 293
is given by 294
ˆη(r) =
ˆgr
−α
ˆ
I
t
+
σ
2
P
,
ˆ
I
t
=
i∈φ
N
t
j=1
ˆ
h
ij
d
−α
i
. (8)
Since both g and ˆg as well as h
i
and
ˆ
h
i
areassumedtobei.i.d,295
P
F,e
(r) can be simplified to 296
P
F,e
(r) = P
ˆgr
−α
ˆ
I
t
+
σ
2
P
> T
= P
3
(T, r). (9)
Let us now derive the CP
r
P
f
(r) of a user in the FFR-aided 297
MU-MIMO system, which can be written as 298
P
F
(r) =P
F,c
(r)P [η
t
(r)>S
th
] + P
F,e
(r)P [η
t
(r)<S
th
] . (10)
Here, the first term denotes the CP
r
contributed by the cell- 299
centre users, while the seco nd term denotes the contribution of 300
the cell-edge users. By using the expression in (7) for P
F,c
(r) 301
and the expression in (9) for P
F,e
(r), (10) can be simpli- 302
fied to 303
P
F
(r) =
i∈ψ
1
1 + max{T, S
th
}r
α
d
−α
i
N
t
e
− max{T,S
th
}r
α
σ
2
P
+ P
3
(T, r) − P
3
(T, r)P
1
(S
th
, r). (11)
Lemma 1: The optimum S
th
(denoted by S
opt,C
)thatmaxi-304
mizes the FFR-aided coverage probability is S
th
= T,andwhen305
the SINR threshold is set to S
opt,c
, the coverage probability of 306
FFR becomes higher than that of FR3. 307
Proof: See Appendix A for the proof. 308
B. Case 2: g and ˆg are Completely Correlated as Well as h
i
309
and
ˆ
h
i
are Also Completely Correlated for all i 310
Note th at the centre CP
r
is the same for both the above 311
Case 1 and for this case, since a user does not change its sub- 312
band, when it becomes a cell-centre user because if η
t
(r) ≥ S
th
313
for a user, then it will continue to experience the same fading 314
power. However, the edge CP
r
is different in Case 1 as well as 315
Case 2, and in this scenario the CP
r
P
F,e
(r) of a cell-edge user, 316
IEEE
Proof
KUMAR et al.: COVER AGE PROBABILITY AND ACHIEVABLE RATE ANALYSIS OF MU-MIMO AND SIMO SYSTEMS 5
who is at a distance of r meters from the BS in our FFR network317
is given by318
P
F,e
(r) =P
ˆη
t
(r)>T|η
t
(r)<S
th
=
P
ˆη
t
(r)>T,η
t
(r)<S
th
P [η
t
(r)<S
th
]
.
(12)
Substituting the value of P
F,c
and P
F,e
from (7) and (12) into319
Eq. (10), the CP
r
P
f
(r) in our FFR network can be written as320
P
F
(r) =
i∈ψ
1
1 + max{T, S
th
}r
α
d
−α
i
N
t
e
− max{T,S
th
}r
α
σ
2
P
+ P
ˆη
t
(r)>T,η
t
(r)<S
th
. (13)
Recall that η
t
(r) and ˆη
t
(r) represent the SINR experienced by a321
user in an FR1 and an FR3 system, respectively. Note that even322
though g and ˆg as well as h
i
and
ˆ
h
i
are completely correlated,323
η
t
(r) is not the same as ˆη
t
(r), because the set of interferers are324
different in the denominator of the η
t
(r) and ˆη
t
(r) expressions325
given in (2) and (8), respectively, i.e., ψ corresponds to the326
set of interferers in the FR1 network, while φ corresponds to327
the set of interferers in the FR3 network. Since g and ˆg are328
completely correlated and h
i
and
ˆ
h
i
are also completely corre-329
lated for all i, we use the following transformation to further330
simplify P
F
(r):331
P
ˆη
t
(r)>T,η
t
(r)<S
th
=P
ˆη
t
(r)>T, ˆη
t
(r)<
ˆ
S
th
. (14)
Basically instead of marking a user as a cell-edge user based
332
on the FR1 SINR η
t
(r), we mark them on the basis of the FR3333
SINR ˆη
t
(r) by introducing a new SINR threshold
ˆ
S
th
.Inother334
words, we introduce a new SINR threshold
ˆ
S
th
for ensuring that335
if for any user we have η
t
(r)<S
th
, then for the same user we336
have ˆη
t
(r)<
ˆ
S
th
and vice-versa. The threshold
ˆ
S
th
is computed337
using the relationship of P[η
t
(r)<S
th
]=P[ˆη
t
(r)<
ˆ
S
th
].This338
ensures that the same user is marked as a cell-edge user for both339
reuse patterns FR1 and FR3. Now, using the transformation340
given in (14), P
F
(r) can be simplified to341
P
F
(r) =
i∈ψ
1
1 + max{T, S
th
}r
α
d
−α
i
N
t
e
− max{T,S
th
}r
α
σ
2
P
+ P
ˆη(r)>T
− P
ˆη(r)>max{
ˆ
S
th
, T}
. (15)
In this case, to obtain the optimum S
opt,C
, we co nsider the342
following two possibilities: (i) S
th
≥ T, (ii) S
th
< T.343
(i) S
th
≥ T: In this scenario, CP
f
(r) can be expressed in344
terms of T as:345
P
F
(r, S
th
≥ T) =
i∈ψ
1
1 + S
th
r
α
d
−α
i
e
−S
th
r
α
σ
2
P
+ P
3
(T, r) − P
3
(
ˆ
S
th
, r). (16)
Since we have P
3
(
ˆ
S
th
, r) = P
1
(S
th
, r) and P
1
(S
th
, r) =346
i∈ψ
1
1+S
th
r
α
d
−α
i
N
t
e
−S
th
r
α
σ
2
P
, hence347
P
F
(r, S
th
≥ T) = P
3
(T, r). (17)
(ii) S
th
< T: In this case P
f
(r) can be formulated in terms 348
of T as: 349
P
F
(r, S
th
< T) =
i∈ψ
1
1 + Tr
α
d
−α
i
N
t
e
−Tr
α
σ
2
P
+ P
3
(T, r) − P
3
max{
ˆ
S
th
, T}, r
. (18)
Note that when S
th
< T,
ˆ
S
th
may be higher or lower than T. 350
When
ˆ
S
th
> T, 351
P
3
max{
ˆ
S
th
, T}, r
=P
3
(
ˆ
S
th
, r) =P
1
(S
th
, r)>P
1
(T, r) (19)
since S
th
< T.Andwhen
ˆ
S
th
< T,wehave: 352
P
3
max{
ˆ
S
th
, T}, r
= P
3
(T, r)>P
1
(T, r). (20)
Hence, we arrive at:
353
P
F
(r, S
th
< T) =
i∈ψ
1
1 + Tr
α
d
−α
i
N
t
e
−Tr
α
σ
2
P
+ P
3
(T, r) − P
3
max{
ˆ
S
th
, T}, r
< P
3
(T, r). (21)
Comparing the FFR CP
r
for S
th
≥ T and S
th
< T given by (17) 354
and (21), respectively, it becomes apparent that P
F
(r, S
th
≥ 355
T)>P
F
(r, S
th
< T). I n other words, when the fading is fully 356
correlated across the sub-bands, the optimal choice of the SINR 357
threshold is S
th
≥ T and at the optimal SINR threshold the FFR 358
scheme succeeds in achieving the FR3 CP
r
. Unlike for Case 1, 359
the FFR CP
r
is not better than the FR3 CP
r
since there is no sub- 360
band diversity gain, when a user moves from the cell-centre to 361
the cell-edge region. 362
In order to find the CP
r
for a typical user, we have to calculate 363
the probability density function (pdf) of r, which is the distanc e 364
between the 0
th
BS (serving BS) and the desired user. To 365
calculate this pdf, we model the cell shape by an inner circle 366
within a hexagonal cell [33], and assume that the users are 367
uniformly distribu ted. Therefore, the pdf f
R
(r) of r is given by 368
f
R
(r) =
2r
R
2
, r R
0, r > R.
(22)
IV. A
VERAGE RATE 369
In this section, we derive the average rate of both the FFR- 370
aided MU-MIMO as well as of its SIMO counterpart and find 371
the optimum value of S
th
(denoted by S
opt,R
) for which the 372
average rate is maximum. The average rate of the system is 373
given by R = E[ln(1 + SINR)]. In order to derive the average 374
rate
5
for the FFR system, we have to consider its sub-band al- 375
location. Since the users are uniformly distributed, the specific 376
sub-band allocated to the cell-centre users and cell-edge users 377
are given by [9], [10] N
c
= N
t
P
F,c
and N
e
=
N
t
−N
c
3
,whereP
F,c
378
denotes the specific fraction of cell-centre users, while N
t
, N
c
379
and N
e
denote the total band, cell-centre sub-band and cell-edge 380
5
An interference limited system is assumed for simplicity, which implies
ignoring the effects of noise. However, the derivation of the average rate can be
readily e xtended to the case, where the thermal noise is also considered.
Figures (6)
Citations
More filters
Journal Article•DOI•

[...]

Xiaohu Ge1, Xiaotong Tian1, Yehong Qiu1, Guoqiang Mao2, Tao Han1 •
Huazhong University of Science and Technology1, University of Technology, Sydney2
21 Jun 2018-IEEE Transactions on Communications
TL;DR: This paper provides a tractable method to investigate the performance of the small-cell networks with fractal coverage characteristics and finds the average achievable rate and area spectral efficiency with anisotropic path loss models have been underestimated in the fractal small- cell networks.
Abstract: To meet massive wireless traffic demand in the future fifth generation (5G) cellular networks, small-cell networks are emerging as an attractive solution for 5G network deployments. The cellular coverage characteristic is a key issue for the deployment of the small-cell networks. Considering the anisotropic path loss in wireless channels of real cellular scenarios, in this paper the fractal coverage characteristic is first used to evaluate the performance of the small-cell networks. Moreover, the coverage probability, average achievable rate, and the area spectral efficiency are derived for fractal small-cell networks. Compared with the average achievable rate and area spectral efficiency with isotropic path loss models, the average achievable rate and area spectral efficiency with anisotropic path loss models have been underestimated in the fractal small-cell networks. Considering the impact of the anisotropic path loss on wireless channels, most of performances of wireless cellular networks need to be re-evaluated. This paper provides a tractable method to investigate the performance of the small-cell networks with fractal coverage characteristics.

28 citations

Cites methods from "Coverage Probability and Achievable..."

  • [...]

  • [...]

Journal Article•DOI•

[...]

Suman Kumar1, Sheetal Kalyani2•
Indian Institute of Technology Ropar1, Indian Institute of Technology Madras2
01 Dec 2017-IEEE Transactions on Wireless Communications
TL;DR: The derived expression for outage probability is derived when the signal-of-interest and interferers both experience $\kappa$ - $\mu$ shadowed fading in an interference limited scenario and can be expressed in terms of Pochhammer integral.
Abstract: The $\kappa$ - $\mu$ shadowed fading model is a very general fading model as it includes both $\kappa$ - $\mu$ and $\eta$ - $\mu$ as special cases. In this paper, we derive the expression for outage probability when the signal-of-interest (SoI) and interferers both experience $\kappa$ - $\mu$ shadowed fading in an interference limited scenario. The derived expression is valid for arbitrary SoI parameters, arbitrary $\kappa$ , and $\mu$ parameters for all interferers and any value of the parameter $m$ for the interferers excepting the limiting value of $m\rightarrow \infty$ . The expression can be expressed in terms of Pochhammer integral, where the integrands of integral only contains elementary functions. The outage probability expression is then simplified for various special cases, especially when SoI experiences $\eta$ - $\mu$ or $\kappa$ - $\mu$ fading. Furthermore, the rate expression is derived when the SoI experiences $\kappa$ - $\mu$ shadowed fading with the integer values of $\mu$ , and the interferers experience $\kappa$ - $\mu$ shadowed fading with arbitrary parameters. The rate expression can be expressed in terms of sum of Lauricella’s function of the fourth kind. The utility of our results is demonstrated by using the derived expression to study and compare fractional frequency reuse and soft frequency reuse in the presence of $\kappa$ - $\mu$ shadowed fading. Extensive simulation results are provided and these further validate our theoretical results.

17 citations

Cites methods from "Coverage Probability and Achievable..."

  • [...]

  • [...]

Journal Article•DOI•

[...]

Suman Kumar1, Sheetal Kalyani1, Krishnamurthy Giridhar1•
Indian Institute of Technology Madras1
01 Aug 2016-IEEE Transactions on Wireless Communications
TL;DR: It is shown that the FFR provides better edge CP and average rate when compared with the SFR in single-input single-output (SISO) networks, thereby suggesting thatThe FFR should be preferred over S FR in cellular SISO OFDMA systems.
Abstract: In soft frequency reuse (SFR) when the user is classified as a cell-center user based on signal-to-interference-plus-noise-ratio in a sub-band, the user retains its sub-band. On the other hand, if the user is classified as a cell-edge user, a new sub-band is allocated. We analyze the impact of correlation between the cell-center sub-band and the cell-edge sub-band for a user when the SFR technique is used in a cellular orthogonal frequency division multiple access (OFDMA) system. The coverage probability (CP) and the average rate are derived for the following two cases: 1) when the sub-bands are independent and 2) when the sub-bands are completely correlated. We show that correlation significantly decreases the edge CP and the average rate of the SFR technique, and as the power control factor increases, the impact of correlation decreases. Fractional frequency reuse (FFR) and SFR techniques are compared and it is shown that the impact of correlation on the FFR is significantly lower. Furthermore, it is also shown that the FFR provides better edge CP and average rate when compared with the SFR in single-input single-output (SISO) networks, thereby suggesting that the FFR should be preferred over SFR in cellular SISO OFDMA systems. However, for single-input multiple-output networks, the SFR provides a better average rate when compared with the FFR, especially when the sub-band correlation is not significant. Finally, the impact of log-normal shadowing has been carefully studied.

15 citations

Cites background or methods from "Coverage Probability and Achievable..."

  • [...]

  • [...]

  • [...]

Journal Article•DOI•

[...]

Jan Garcia-Morales1, Guillem Femenias1, Felip Riera-Palou1•
University of the Balearic Islands1
01 Apr 2018-IEEE Transactions on Vehicular Technology
TL;DR: This paper presents a novel optimal fifth-percentile user rate constrained design for FFR/SFR-based networks that clearly outperforms previous schemes in terms of throughput fairness control due to a more rational compromise between average cell throughput and cell-edge ICIC.
Abstract: Interference mitigation strategies are deemed to play a key role in the context of the next generation (B4G/5G) of multicellular networks based on orthogonal frequency division multiple access. Fractional and soft frequency reuse (FFR, SFR) constitute two powerful mechanisms for intercell interference coordination that have been already adopted by emerging cellular deployments as an efficient way to improve the throughput performance perceived by cell-edge users. This paper presents a novel optimal fifth-percentile user rate constrained design for FFR/SFR-based networks that, by appropriately dimensioning the center and edge regions of the cell, rightly splitting the available bandwidth among these two areas while assigning the corresponding transmit power, allows a tradeoff between cell throughput performance and fairness to be established. To this end, both the cumulative distribution function of the user throughput and the average spectral efficiency of the system are derived assuming the use of the ubiquitous proportional fair scheduling policy. The mathematical framework is then used to obtain numerical results showing that the novel proposed design clearly outperforms previous schemes in terms of throughput fairness control due to a more rational compromise between average cell throughput and cell-edge ICIC.

7 citations

Journal Article•DOI•

[...]

Seok-Ho Chang1, Hee-Gul Park2, Sang-Hyo Kim3, Jihwan P. Choi4•
Dankook University1, Ericsson2, Sungkyunkwan University3, Daegu Gyeongbuk Institute of Science and Technology4
24 Jul 2018-IEEE Transactions on Communications
TL;DR: It is proved that the optimal Full FR coverage is a non-increasing function of BS power when the powers of all BSs in the network are scaled up or down at the same rate.
Abstract: A fractional frequency reuse (FFR) system is an inter-cell interference coordination scheme used in cellular networks. In FFR systems, the available bandwidth is partitioned into orthogonal subbands such that the users near the cell center adopt subbands of a frequency reuse (FR) factor equal to one (i.e., Full FR), and the users near the cell edge adopt the subbands of an FR factor greater than one (i.e., Partial FR). The proper design of Full FR coverage, which is used to distinguish Full FR regions from Partial FR regions, plays a critical role in FFR system performance. This paper studies the optimal Full FR coverage that maximizes system throughput in the downlink in multiple-input multiple-output (MIMO) cellular networks. For MIMO systems, orthogonal space–time block codes are considered. We analytically compare the outage probabilities of Full FR and Partial FR for a given user’s location, where the outage probability is evaluated through small-scale multipath fading. By doing so, subject to the constraint that a given target outage probability (quality-of-service) is satisfied, the optimal Full FR coverage is analyzed as a function of base station (BS) power. We prove that the optimal Full FR coverage is a non-increasing function of BS power when the powers of all BSs in the network are scaled up or down at the same rate. This result offers insight into the design of Full FR coverage in relation to BS power; we gain insight into the complicated relationship between crucial FFR design parameters.

7 citations

References
More filters
Book•

[...]

David Tse1, Pramod Viswanath2•
University of California, Berkeley1, University of Illinois at Urbana–Champaign2
01 Jan 2005
TL;DR: In this paper, the authors propose a multiuser communication architecture for point-to-point wireless networks with additive Gaussian noise detection and estimation in the context of MIMO networks.
Abstract: 1. Introduction 2. The wireless channel 3. Point-to-point communication: detection, diversity and channel uncertainty 4. Cellular systems: multiple access and interference management 5. Capacity of wireless channels 6. Multiuser capacity and opportunistic communication 7. MIMO I: spatial multiplexing and channel modeling 8. MIMO II: capacity and multiplexing architectures 9. MIMO III: diversity-multiplexing tradeoff and universal space-time codes 10. MIMO IV: multiuser communication A. Detection and estimation in additive Gaussian noise B. Information theory background.

7,400 citations

Book•

[...]

Stefania Sesia, Issam Toufik, Matthew Baker
29 Aug 2011
TL;DR: Scrase et al. as discussed by the authors provide a comprehensive system-level understanding of LTE, built on explanations of the theories which underlie it, and provide a broad, balanced and reliable perspective on this important technology Lucid yet thorough, the book devotes particular effort to explaining the theoretical concepts in an accessible way.
Abstract: Where this book is exceptional is that the reader will not just learn how LTE works but why it works Adrian Scrase, ETSI Vice-President, International Partnership Projects LTE - The UMTS Long Term Evolution: From Theory to Practice provides the reader with a comprehensive system-level understanding of LTE, built on explanations of the theories which underlie it The book is the product of a collaborative effort of key experts representing a wide range of companies actively participating in the development of LTE, as well as academia This gives the book a broad, balanced and reliable perspective on this important technology Lucid yet thorough, the book devotes particular effort to explaining the theoretical concepts in an accessible way, while retaining scientific rigour It highlights practical implications and draws comparisons with the well-known WCDMA/HSPA standards The authors not only pay special attention to the physical layer, giving insight into the fundamental concepts of OFDMA, SC-FDMA and MIMO, but also cover the higher protocol layers and system architecture to enable the reader to gain an overall understanding of the system Key Features: Draws on the breadth of experience of a wide range of key experts from both industry and academia, giving the book a balanced and broad perspective on LTE Provides a detailed description and analysis of the complete LTE system, especially the ground-breaking new physical layer Offers a solid treatment of the underlying advances in fundamental communications and information theory on which LTE is based Addresses practical issues and implementation challenges related to the deployment of LTE as a cellular system Includes an accompanying website containing a complete list of acronyms related to LTE, with a brief description of each (http://wwwwileycom/go/sesia_theumts) This book is an invaluable reference for all research and development engineers involved in LTE implementation, as well as graduate and PhD students in wireless communications Network operators, service providers and R&D managers will also find this book insightful

3,434 citations

Journal Article•DOI•

[...]

Quentin H. Spencer1, A.L. Swindlehurst1, Martin Haardt2•
Brigham Young University1, Technische Universität Ilmenau2
01 Feb 2004-IEEE Transactions on Signal Processing
TL;DR: While the proposed algorithms are suboptimal, they lead to simpler transmitter and receiver structures and allow for a reasonable tradeoff between performance and complexity.
Abstract: The use of space-division multiple access (SDMA) in the downlink of a multiuser multiple-input, multiple-output (MIMO) wireless communications network can provide a substantial gain in system throughput. The challenge in such multiuser systems is designing transmit vectors while considering the co-channel interference of other users. Typical optimization problems of interest include the capacity problem - maximizing the sum information rate subject to a power constraint-or the power control problem-minimizing transmitted power such that a certain quality-of-service metric for each user is met. Neither of these problems possess closed-form solutions for the general multiuser MIMO channel, but the imposition of certain constraints can lead to closed-form solutions. This paper presents two such constrained solutions. The first, referred to as "block-diagonalization," is a generalization of channel inversion when there are multiple antennas at each receiver. It is easily adapted to optimize for either maximum transmission rate or minimum power and approaches the optimal solution at high SNR. The second, known as "successive optimization," is an alternative method for solving the power minimization problem one user at a time, and it yields superior results in some (e.g., low SNR) situations. Both of these algorithms are limited to cases where the transmitter has more antennas than all receive antennas combined. In order to accommodate more general scenarios, we also propose a framework for coordinated transmitter-receiver processing that generalizes the two algorithms to cases involving more receive than transmit antennas. While the proposed algorithms are suboptimal, they lead to simpler transmitter and receiver structures and allow for a reasonable tradeoff between performance and complexity.

3,117 citations

"Coverage Probability and Achievable..." refers background in this paper

  • [...]

Journal Article•DOI•

[...]

David Gesbert1, Marios Kountouris1, Robert W. Heath2, Chan-Byoung Chae2, Thomas Salzer3 •
Institut Eurécom1, University of Texas at Austin2, Orange S.A.3
15 Oct 2007-IEEE Signal Processing Magazine
TL;DR: Multi-user MIMO (MU-MIMO) networks reveal the unique opportunities arising from a joint optimization of antenna combining techniques with resource allocation protocols, and brings robustness with respect to multipath richness, yielding the diversity and multiplexing gains without the need for multiple antenna user terminals.
Abstract: Multi-user MIMO (MU-MIMO) networks reveal the unique opportunities arising from a joint optimization of antenna combining techniques with resource allocation protocols. Furthermore, it brings robustness with respect to multipath richness, allowing for compact antenna spacing at the BS and, crucially, yielding the diversity and multiplexing gains without the need for multiple antenna user terminals. To realize these gains, however, the BS should be informed with the user's channel coefficients, which may limit practical application to TDD or low-mobility settings. To circumvent this problem and reduce feedback load, combining MU-MIMO with opportunistic scheduling seems a promising direction. The success for this type of scheduler is strongly traffic and QoS-dependent, however.

1,058 citations

Journal Article•DOI•

[...]

David Astely1, Erik Dahlman1, Anders Furuskär1, Ylva Jading1, Magnus Lindström1, Stefan Parkvall1 •
Ericsson1
01 Apr 2009-IEEE Communications Magazine
TL;DR: An overview of the LTE radio interface, recently approved by the 3GPP, together with a more in-depth description of its features such as spectrum flexibility, multi-antenna transmission, and inter-cell interference control are provided.
Abstract: This article provides an overview of the LTE radio interface, recently approved by the 3GPP, together with a more in-depth description of its features such as spectrum flexibility, multi-antenna transmission, and inter-cell interference control. The performance of LTE and some of its key features is illustrated with simulation results. The article is concluded with an outlook into the future evolution of LTE.

862 citations

"Coverage Probability and Achievable..." refers background in this paper

  • [...]

  • [...]

Related Papers (5)

[...]

19 Mar 2015-IEEE Transactions on Wireless Communications
T. Lakshmi Narasimhan, P. Raviteja, Ananthanarayanan Chockalingam

[...]

16 Dec 2008-arXiv: Information Theory
Jun Zhang, Robert W. Heath, Marios Kountouris, Jeffrey G. Andrews 

[...]

15 Apr 2008
Peng Lu, Hong-Chuan Yang, Young-Chai Ko

[...]

17 Oct 2011-IEEE Transactions on Wireless Communications
Thomas David Novlan, Radha Krishna Ganti, Arunabha Ghosh, Jeffrey G. Andrews 

[...]

15 Sep 2014-IEEE Transactions on Communications
Azwan Mahmud, Khairi Ashour Hamdi
Frequently Asked Questions (1)
Q1. What are the contributions in "Coverage probability and achievable rate analysis of ffr-aided multi-user ofdm-based mimo and simo systems" ?

In 8 particular, given a reuse region of 3 ( FR3 ) and a reuse region of 9 1 ( FR1 ) as well as a signal-to-interference-plus-noise-ratio ( SINR ) 10 threshold Sth, which decides the user assignment to either the FR1 11 or FR3 regions, the authors theoretically show that: 1 ) the optimal choice 12 of Sth which maximizes the coverage probability is Sth = T, where 13 T is the target SINR required for ensuring adequate coverage, and 14 2 ) the optimal choice of Sth which maximizes the average rate is 15 given by Sth = 21 Furthermore, the performance of their FFR-aided MU-MIMO and 22 SIMO systems is compared.