PHYSICAL REVIEW A 96, 042327 (2017)
Detecting metrologically useful asymmetry and entanglement by a few local measurements
Chao Zhang,
1,2
Benjamin Yadin,
3
Zhi-Bo Hou,
1,2
Huan Cao,
1,2
Bi-Heng Liu,
1,2
Yun-Feng Huang,
1,2,*
Reevu Maity,
3
Vlatko Vedral,
3,4
Chuan-Feng Li,
1,2,†
Guang-Can Guo,
1,2
and Davide Girolami
3,‡
1
Key Laboratory of Quantum Information, University of Science and Technology of China, CAS, Hefei, 230026, China
2
Synergetic Innovation Center of Quantum Information and Quantum Physics, University of Science and Technology of China,
Hefei, 230026, People’s Republic of China
3
Department of Atomic and Laser Physics, University of Oxford, Parks Road, Oxford OX1 3PU, United Kingdom
4
Centre for Quantum Technologies, National University of Singapore, 117543, Singapore
(Received 19 May 2017; revised manuscript received 4 July 2017; published 19 October 2017)
Important properties of a quantum system are not directly measurable, but they can be disclosed by how fast
the system changes under controlled perturbations. In particular, asymmetry and entanglement can be verified
by reconstructing the state of a quantum system. Yet, this usually requires experimental and computational
resources which increase exponentially with the system size. Here we show how to detect metrologically useful
asymmetry and entanglement by a limited number of measurements. This is achieved by studying how they affect
the speed of evolution of a system under a unitary transformation. We show that the speed of multiqubit systems
can be evaluated by measuring a set of l ocal observables, providing exponential advantage with respect to state
tomography. Indeed, the presented method requires neither the knowledge of the state and the parameter-encoding
Hamiltonian nor global measurements performed on all the constituent subsystems. We implement the detection
scheme in an all-optical experiment.
DOI: 10.1103/PhysRevA.96.042327
I. INTRODUCTION
Quantum coherence and entanglement can generate non-
classical speedup in information processing [1]. Yet, their
experimental verification is challenging. Being not directly
observable, their detection usually implies reconstructing
the full state of the system, which r equires a number of
measurements growing exponentially with the system size [2].
Also, verifying their presence is necessary, but not sufficient
to guarantee a computational advantage.
Here we show how to detect useful coherence and en-
tanglement in systems of arbitrary dimension by a limited
sequence of measurements. We propose an experimentally
friendly measure of the speed of a quantum system, i.e., how
fast its state changes under a generic channel, which for n-qubit
systems is a function of a linearly scaling [O(n)] number
of observables. The speed of a quantum system determines
its computational power [3–6]. Quantum speed limits of
open systems also provide information about the environment
structure [7–9], helping develop efficient control strategies
[10–13], and investigate phase transitions of condensed matter
systems [14,15]. We prove a quantitative link between our
speed measure, when undertaking a unitary dynamics, and
metrological quantum resources. In Sec. II, we relate speed to
asymmetry, i.e., the coherence with respect to a Hamiltonian
eigenbasis. Asymmetry underpins the usefulness of a probe
to phase estimation and reference frame alignment [16–19].
Moreover, a superlinear scaling of the speed of multipartite
systems certifies an advantage in metrology powered by
entanglement, as discussed in Sec. III.Weshowhowto
detect asymmetry and entanglement by comparing the speed
of two copies of a system, while performing a phase encoding
*
hyf@ustc.edu.cn
†
cfli@ustc.edu.cn
‡
davegirolami@gmail.com
dynamics on only one copy. An important advantage of
the method is that aprioriknowledge of the input state
and the Hamiltonian is not required. We demonstrate the
scheme in an all-optical experiment, described in Sec. IV.
An asymmetry lower bound and an entanglement witness are
extracted from the speed of a two-qubit system in dynamics
generated by additive spin Hamiltonians, without brute force
state reconstruction. In Sec. V, we provide for the interested
reader a brief review of information geometry concepts and
the complete proofs of the theoretical results. We draw our
conclusions in Sec. VI.
II. RELATING ASYMMETRY TO OBSERVABLES
The sensitivity of a quantum system to a quantum operation
described by a parametrized channel
t
[1], where t is the time,
is determined by how fast its state ρ
t
:=
t
(ρ
0
)evolves.We
quantify the system speed over an interval 0 t τ by the
average rate of change of the state, which is given by mean
values of quantum operators ·
ρ
t
= Tr(·ρ
t
):
s
τ
(ρ
t
):=
||ρ
τ
− ρ
0
||
2
τ
=
(ρ
τ
ρ
τ
+ρ
0
ρ
0
− 2ρ
τ
ρ
0
)
1/2
τ
, (1)
where the Euclidean distance is employed. Measuring the
swap operator on two system copies is sufficient to quan-
tify state overlaps, σ
ρ
=V
ρ⊗σ
,V (|φ
1
⊗|φ
2
) =|φ
2
⊗
|φ
1
,∀|φ
1,2
. The global swap is the product of local
swaps, V
S
=⊗
n
i=1
V
S
i
. Then, for n-qubit systems S ≡{S
i
},i =
1,...,n, a state overlap σ
S
ρ
S
is obtained by evaluating O(n)
observables, one for each pair of subsystem S
i
copies [20–22].
Each local swap can be recast i n terms of projections on the
Bell singlet V
S
i
= I
d
2
− 2
ψ
−
S
i
,
ψ
−
S
i
=|ψ
−
ψ
−
|
S
i
,|ψ
−
=
1/
√
2(|01−|10), a standard routine of quantum information
processing, e.g., in bosonic lattices. Bell state projections
2469-9926/2017/96(4)/042327(10) 042327-1 ©2017 American Physical Society

CHAO ZHANG et al. PHYSICAL REVIEW A 96, 042327 (2017)
are implemented by n beam splitters interfering each pair
of S
i
copies, and coincidence detection on the correlated
pairs. Hence the s peed of an n-qubit system is evaluated
by networks whose size scales linearly with the number of
subsystems, employing O(n) two-qubit gates and detectors.
Note that tomography demands to prepare O(2
2n
)system
copies and perform a measurement on each of them [2]. It
is also possible to extract the swap value by single qubit
interferometry [23–25]. The two copies of the system are
correlated with an ancillary qubit by a controlled-swap gate.
The mean value of the swap is then encoded in the ancilla
polarization. Yet, the implementation of a controlled-swap gate
is currently a serious challenge [26].
Crucial properties of quantum systems can be determined
by measuring the speed defined in Eq. (1), without further data.
Performing a quantum computation U
t
ρU
†
t
,U
t
= e
−iHt
, relies
on the coherence in the Hamiltonian H eigenbasis, a property
called [U(1)] asymmetry [16–19]. In fact, incoherent states
in such a basis do not evolve. Asymmetry is operationally
defined as the system ability to break a symmetry generated
by the Hamiltonian. Asymmetry measures are defined as
nonincreasing functions in symmetry-preserving dynamics,
which are modeled by transformations commuting with
the Hamiltonian evolution, [,U
t
] = 0.
Experimentally measuring coherence, and in particular
asymmetry, is hard [27,28]. One cannot discriminate with
certainty coherent states from incoherent mixtures, without full
state reconstruction. We show how to evaluate the asymmetry
of a system by its speed (full details and proofs in Sec. V).
To quantify the sensitivity of a probe state ρ =
i
λ
i
|ii|
to the unitary transformation U
t
, we employ the symmetric
logarithmic derivative quantum Fisher information (SLDF), a
widely employed quantity in quantum metrology and quantum
information [29]:
I
F
(ρ,H) = 1/2
i,j
(λ
i
− λ
j
)
2
λ
i
+ λ
j
|i|H |j|
2
. (2)
Note that the SLDF is one of the many quantum extensions
of the classical Fisher information [30]. Indeed, the SLDF
is an ensemble asymmetry monotone, i.e., an asymmetry
measure, being contractive on average under commuting oper-
ations [31]:
I
F
(ρ,H)
μ
p
μ
I
F
(
μ
(ρ),H ),
∀{p
μ
,
μ
} :
μ
p
μ
= 1, [
μ
,U
t
] = 0. (3)
We observe that this implies that every quantum Fisher
information is an asymmetry ensemble monotone; see Sec. V.
Reconstructing both state and Hamiltonian is required to
compute the SLDF. Yet, few algebra steps show that it is
lower bounded by the squared speed over an interval τ of the
evolution U
t
ρU
†
t
:
S
τ
(ρ,H):= s
τ
(ρ)
2
/2 =
ρ
ρ
−U
τ
ρU
†
τ
ρ
τ
2
,
(4)
S
τ
(ρ,H) I
F
(ρ,H), ∀ρ,τ,H,
where we drop the time label, as the speed is constant. It
is then possible to bound asymmetry with respect to an
arbitrary Hamiltonian by evaluating the purity ρ
ρ
and the
overlap U
τ
ρU
†
τ
ρ
. A nonvanishing speed reliably witnesses
asymmetry, s
τ
(ρ) > 0 ⇐⇒ I
F
(ρ,H) > 0,∀τ . The Hamil-
tonian variance is an upper bound to asymmetry, up to
a constant, I
F
(ρ,H) V(ρ,H) =H
2
ρ
−H
2
ρ
,∀ρ,H.Yet
the variance is generally not a reliable indicator of asymmetry,
as it is arbitrarily large for incoherent mixed states. The chain
of inequalities is saturated for pure states, in the zero time limit,
lim
τ →0
S
τ
(ρ
ψ
,H ) = I
F
(ρ
ψ
,H ) = V(ρ
ψ
,H ),ρ
ψ
=|ψψ|.
In fact, the quantum Fisher information quantifies the
instantaneous response to a perturbation [11,30].
III. WITNESSING METROLOGICALLY
USEFUL ENTANGLEMENT
We extend the analysis to multipartite systems, proving
that nonlinear speed scaling witnesses useful entanglement.
Consider a phase estimation protocol, a building block of
quantum computation and metrology schemes [1,3,11]. A
phase shift U
τ,i
= e
−ih
i
τ
is applied in parallel to each site
of an n-qubit probe. The generator is an additive Hamiltonian
H
n
=
n
i=1
h
i
,h
i
= I
1,...,i−1
⊗ σ
i
⊗ I
i+1,...,n
, where σ is an
arbitrary spin-1/2 operator. The goal is to estimate the
parameter τ by an estimator τ
est
, extracted from measurements
on the perturbed system. The quantum Cramér-Rao bound
establishes that asymmetry, measured by the SLDF, bounds
the estimation precision, expressed via the estimator variance,
V(ρ,τ
est
) [νI
F
(ρ,H
n
)]
−1
,∀ρ,H
n
, where ν is the number of
trials, and the estimation is assumed unbiased, τ
est
ρ
= τ.
Separable states achieve at best I
F
(ρ,H
n
) = O(n), while
entanglement asymptotically enables up to a quadratic im-
provement, I
F
(ρ,H
n
) = O(n
2
),n →∞. Specifically, with the
adopted normalization, the relation I
F
(ρ,H
n
) >n/4, i.e.,
superlinear asymmetry with respect to an additive observable,
witnesses entanglement [32]. Given Eq. (4), entanglement-
enhanced precision in estimating a phase shift τ is verified if
S
τ
(ρ,H
n
) >n/4. (5)
The overlap detection network for n-qubit systems and
additive Hamiltonians is depicted in Fig. 1. Evaluating the
SLDF is an appealing strategy to verify an advantage given by
entanglement, rather than just detecting quantum correlations
[22,33–38]. The SLDF of thermal states can be extracted
by measuring the system dynamic susceptibility [39], while
lower bounds are obtained by two-time detections of a global
observable [40,41]. Also, collective observables can witness
entanglement in highly symmetric states [42]. Our proposal
has two peculiar advantages. First, it is applicable to any probe
state ρ without aprioriinformation and assumptions, e.g.,
invariance under permutation of the subsystems. Second, only
local pairwise interactions and detections are needed. This
means that distant laboratories can verify quantum speedup
due to entanglement in a shared system S by local operations
and classical communication [1], providing each laboratory
with two copies of a subsystem S
i
. Note that quadratic speed
042327-2

DETECTING METROLOGICALLY USEFUL ASYMMETRY AND . . . PHYSICAL REVIEW A 96, 042327 (2017)
S
1
ρ
S
1
ρ
S
2
ρ
S
2
ρ
S
n
ρ
S
n
ρ
τ,1
U
U
BS
U
BS
U
BS
τ,2
U
τ,n
U
FIG. 1. Overlap detection. The network evaluates the overlap
e
−iH
n
τ
ρ
2
S
e
iH
n
τ
ρ
1
S
,H
n
=
n
i=1
h
i
, in an n-qubit system S ≡{S
i
}.
Each pair of subsystem S
i
copies, in the state ρ
1
S
i
⊗ ρ
2
S
i
,enters
a two-arm channel (blue and green). The unitaries U
τ,i
= e
−ih
i
τ
are applied to the second copy of each pair. Leaving both copies
unperturbed, the network measures the state purity. The measurement
apparatus (red) interferes each pair of subsystem copies by O(n) beam
splitter gates U
BS
[20]. The overlap, and therefore the speed function
in Eq. (4), is extracted by O(n) local detections.
scaling certifies the probe optimization, S
τ
(ρ,H
n
) = O(n
2
) ⇒
I
F
(ρ,H
n
) = O(n
2
).
IV. EXPERIMENTAL ASYMMETRY
AND ENTANGLEMENT DETECTION
A. Implementation
We experimentally extract a lower bound to metrologically
useful asymmetry and entanglement of a two-qubit system
AB in an optical setup, by measuring its speed during a
unitary evolution. While employing state tomography would
require fifteen measurements, we verify that the proposed
protocol needs six. The system is prepared in a mixture of
Bell states, ρ
p,AB
= p|φ
+
φ
+
|+(1 − p)|φ
−
φ
−
|, |φ
±
=
1/
√
2(|00±|11),p∈ [0,1]. We implement transformations
generated by the Hamiltonians H
2
=
i=A,B
h
i
,h= σ
x,y,z
,
where σ
x,y,z
are the spin-1/2 Pauli matrices, for equally stepped
values of the mixing parameter, p = 0,0.1,0.2,...,0.9,1, over
an interval τ = π/6. The squared speed function S
π/6
(ρ
p
,H
2
)
is evaluated from purity and overlap measurements.
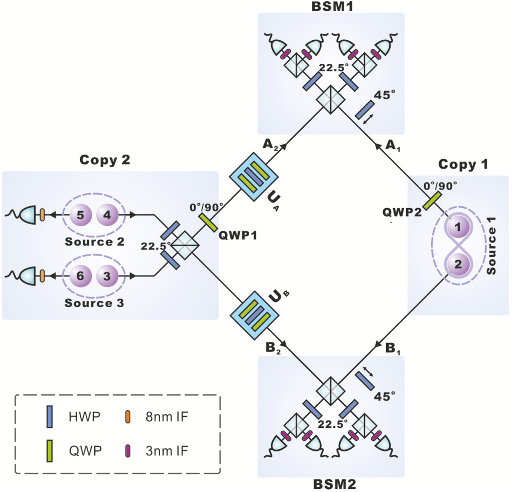
Each run of the experiment implements the scheme in
Fig. 2. We prepare two copies (Copy 1,2) of a maximally
entangled two-qubit state |φ
+
=1/
√
2(HH + VV), where
H,V label horizontal and vertical photon polarizations,
from three spontaneous parametric down-conversion sources
(SPDC Source 1,2,3). They are generated by ultrafast 90 mW
pump pulses from a mode-locked Ti:sapphire laser, with a
central wavelength of 780 nm, a pulse duration of 140 fs,
and a repetition rate of 76 MHz. Copy 1 (photons 1,2)
FIG. 2. Experimental setup. We prepare two copies of a Bell
state |φ
+
by a laser-emitted ultraviolet pulse split into three beams
pumping SPDC s ources. The scheme guarantees that both copies are
emitted by different sources. Conversely, in a two source setting, the
fourfold coincidences in the B SMs could be generated by two photon
pairs emitted from a single source, invalidating the experiment. The
four terms of the mixture are obtained by rotating QWP1,2. Purity
and overlap measurements are implemented via BSM schemes. A
multichannel unit counts the sixfold coincidences (one detector fire
in each output mode).
is obtained from Source 1, by employing a sandwichlike
beta-barium borate (BBO) crystal [43]. Copy 2 is prepared
from Source 2,3. Two photon pairs (photons 3–6) are
generated via single BBO crystals (beamlike type-II phase
matching). By detecting photons 5,6, a product state encoded
in photons 3,4 is triggered. Photons 3–4 polarizations
are rotated via half-wave plates (HWPs). They are then
interfered by a polarizing beam splitter (PBS) for parity
check measurements. We then simulate the preparation of the
state ρ
1
p
⊗ ρ
2
p
= p
2
φ
+
φ
+
12
+ p(1 − p)(
φ
+
φ
−
12
+
φ
−
φ
+
12
) +
(1 − p)
2
φ
−
φ
−
12
,
φ
±
φ
±
12
=|φ
±
φ
±
|
A
1
B
1
⊗|φ
±
φ
±
|
A
2
B
2
.
Classical mixing is obtained by applying quarter-wave plates
(QWP1,QWP2) to each system copy. A 90
◦
rotated QWP
swaps the Bell states, |φ
±
→|φ
∓
, generating a π phase shift
between H,V polarizations. The four terms of the mixture are
obtained in separate runs by engineering the rotation sequences
(QWP1,QWP2) ={(0
◦
,0
◦
),(0
◦
,90
◦
),(90
◦
,0
◦
),(90
◦
,90
◦
)},
with a duration proportional to {p
2
,p(1 − p),p(1 − p),(1 −
p)
2
}, respectively. The collected data from the four cases are
then identical to the ones obtained from direct preparation of
the mixture.
We quantify the speed by measuring the purity V
12
ρ
1
p
⊗ρ
2
p
and the overlap V
12
ρ
1
p
⊗U
π/6
ρ
2
p
U
†
π/6
. The unitary gate U
π/6
=
U
π/6,A
2
⊗ U
π/6,B
2
,U
π/6,A
2
(B
2
)
= e
−ih
A
2
(B
2
)
π/6
is applied to the
second system copy by a sequence of one HWP sandwiched
by two QWPs. The sequences of gates implementing each
042327-3

CHAO ZHANG et al. PHYSICAL REVIEW A 96, 042327 (2017)
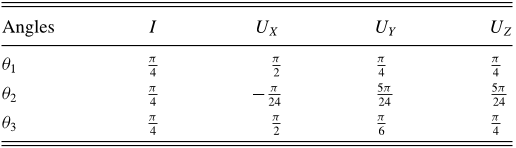
TABLE I. Angles of the wave plates implementing the unitary
gates.
Angles IU
X
U
Y
U
Z
θ
1
π
4
π
2
π
4
π
4
θ
2
π
4
−
π
24
5π
24
5π
24
θ
3
π
4
π
2
π
6
π
4
Hamiltonian are obtained as follows. Single qubit unitary gates
implement SU(2) group transformations. We parametrize the
rotations by the Euler angles (ξ,η,ζ):
u(ξ,η,ζ):= exp
−i
1
2
ξσ
y
exp
−i
1
2
ησ
x
× exp
−i
1
2
ζσ
y
, (6)
where σ
x,y,z
are the Pauli matrices. One can engineer arbi-
trary single qubit gates by a θ -rotated HWP implementing
the transformation H
θ
, sandwiched by two rotated QWPs
(transformations Q
θ
):
u(ξ,η,ζ) = Q
θ
3
H
θ
2
Q
θ
1
, (7)
where θ
1,2,3
are the rotation angles to apply to each plate [44].
In particular, any unitary transformation is prepared by a gate
sequence of the form
θ
1
= π/4 − ζ/2 mod π,
θ
2
=−π/4 + (ξ + η − ζ )/4 mod π,
θ
3
= π/4 + ξ/2 mod π. (8)
The phase shift angles characterizing the Hamiltonian evolu-
tions studied in our experiment are shown in Table I.
The mean value of the swap operator is extracted by
local and bilocal projections on the Bell singlet: V
12
=
I
12
− 2
ψ
−
1
⊗ I
2
− 2I
1
⊗
ψ
−
2
+ 4
ψ
−
ψ
−
12
. That is, three pro-
jections are required for evaluating purity and overlap,
respectively. Note that for n qubits O(2
n
) projections are
required, still having exponential advantage with respect to
full tomography. The projections are obtained via Bell state
measurement (BSM) schemes applied to each subsystem pair.
The BSMs consist of PBSs, HWPs, and photon detectors. We
place a 45
◦
HWP in the input ports of the PBS corresponding
to the A
1
,B
1
subsystems to deterministically project into the
Bell singlet [45]. All the photons pass through single mode
fibers for spatial mode selection. For spectral mode selection,
photons 1–4 (5,6) pass through 3 nm (8 nm) bandwidth filters.
The theoretical values to be extracted are given in Table II.
The experimental results are reported in Fig. 3. For each Hamil-
tonian, we reconstruct the speed function S
π/6
(ρ
p
,H
2
) from
purity and overlap measurements, and compare it against the
values obtained by state tomography of the two system copies.
By Eq. (5), entanglement is detected by superlinear speed
scaling S
π/6
(ρ
p
,H
2
) 1/2. We observe that speed values
above the threshold detect entanglement yielding nonclassical
precision in phase estimation, not just nonseparability of the
density matrix (the state ρ
p
is entangled for p = 1/2).
B. Diagnostic of the experimental setup
1. Error sources
We discuss the efficiency of the experimental setup. The
four photons interfering into the BSMs form a closed-loop
network (Fig. 2). This poses the problem to rule out the case
of BSMs measuring two photon pairs emitted by a single SPDC
source [46]. We guarantee to generate the two system copies
from different sources by preparing Copy 2 from two photon
pair sources by postselection. Single source double down
conversion can also occur because of high-order emission
noise, which has been minimized by setting a low pump
power. The coincidences have been counted by a multichannel
unit, with a 50 h rate for about 6 h in each experiment run.
Here the main error source is the imperfection of the three
Hang-Ou-Mandel interferometers (one for the PBS and each
BSM), which have a visibility of 0.91. This is due to the
temporal distinguishability between the interfering photons,
determined by the pulse duration. The 3 nm and 8 nm
narrow-band filters were placed in front of each detector to
increase the photon overlap.
2. Tomography of the input Bell state copies
We perform full state reconstruction of the two copies
(Copy 1,2) of the Bell states φ
±
1,2
obtained by SPDC sources.
The fidelity of the input states are respectively 0.9889 ( φ
+
1
),
0.9901 (φ
−
1
), 0.9279 (φ
+
2
), and 0.9319 (φ
−
2
). We recall that
Copy 1 (subsystems A
1
B
1
) is generated by the sandwichlike
Source 1 (photons 1,2), while Copy 2 (A
2
B
2
) is triggered by
Sources 2,3 via parity check gate and postselection applied to
two product states (photons 3–6). The counting rate for the
Copy 1 photon pair is 32 000 s, while for the four photons of
Copy 2 is 110 s. We use the maximum likelihood estimation
TABLE II. Theoretical values. The table reports the theoretical values of the SLDF, which is the smallest quantum Fisher information
(multiplying it by a constant turns it into the biggest one; see Sec. V), the lower bound S
τ
(ρ
p
,H
2
) [Eq. (4)], and the related entanglement
witness conditions [Eq. (5)], for the Bell state mixture ρ
p
and the spin Hamiltonians H
2
.
hσ
x
σ
y
σ
z
I
F
(ρ
p
,H
2
) p (1 − p)(1− 2p)
2
S
τ
(ρ
p
,H
2
)(p sin τ/4τ )
2
[(1 − p)sinτ/4τ ]
2
[(1 − 2p)sinτ/4τ ]
2
I
F
(ρ
p
,H
2
) > 0.5 p>0.5 p<0.5 p<0.147,p > 0.853
S
π/6
(ρ
p
,H
2
) > 0.5 p>0.741 p<0.259 p<0.129,p > 0.870
042327-4

DETECTING METROLOGICALLY USEFUL ASYMMETRY AND . . . PHYSICAL REVIEW A 96, 042327 (2017)
1
2
0 0.2 0.4 0.6 0.8 10
0
0.2
0.4
0.6
0.8
1
(a) (b) (c)
p
Speed X
1
2
0 0.2 0.4 0.6 0.8 10
0
0.2
0.4
0.6
0.8
1
p
Speed Y
1
2
0 0.2 0.4 0.6 0.8 10
0
0.2
0.4
0.6
0.8
1
p
Speed Z
FIG. 3. Experimental results. We evaluate the speed of a two-qubit system in the state ρ
p
= p|φ
+
φ
+
|+(1 − p)|φ
−
φ
−
|, for unitary
evolutions U
τ
ρ
p
U
†
τ
,U
τ
= e
−iH
2
τ
,H
2
= σ
x,y,z A
⊗ I
B
+ I
A
⊗ σ
x,y,z B
, over an interval τ = π/6. In (a)–(c), the blue continuous line is the
theoretical speed function S
π/6
(ρ
p
,H
2
), which we aim at reconstructing, while the blue points are the experimental values extracted from purity
and overlap measurements, for p = 0,0.1,0.2,...,0.9,1. The error bars are determined by Monte Carlo simulation with Poisson-distributed
error (1000 samples for each point). For comparison, the two green dashed lines depict the speed function computed from the reconstructed
states of copy 1,2 (the density matrices are reported in the main text), respectively. Superlinear scaling due to entanglement is detected for
values above the horizontal, black dotted line.
method to reconstruct the related density matrices, which read
φ
+
1
=
⎛
⎜
⎜
⎜
⎝
0.5146 + 0.0000i −0.0158 + 0.0031i 0.0058 + 0.0029i 0.4923 + 0.0071i
−0.0158 − 0.0031i 0.0039 + 0.0000i −0.0003 − 0.0026i −0.0173 − 0.0021i
0.0058 − 0.0029i −0.0003 + 0.0026i 0.0029 + 0.0000i 0.0029
− 0.0043i
0.4923 − 0.0071i −0.0173 + 0.0021i 0.0029 + 0.0043i 0.4787 + 0.0000i
⎞
⎟
⎟
⎟
⎠
,
φ
−
1
=
⎛
⎜
⎜
⎜
⎝
0.5072 + 0.0000i −0.0065 + 0.0008i −0.0052 + 0.0028i −0.4931 − 0.0090i
−0.0065 − 0.0008i 0.0030 + 0.0000i 0.0007 + 0.0021i 0.0065 + 0.0016i
−0.0052 − 0.0028i 0.0007 − 0.0021i 0.0029 + 0.0000i 0.0056
+ 0.0034i
−0.4931 + 0.0090i 0.0065 − 0.0016i 0.0056 − 0.0034i 0.4869 + 0.0000i
⎞
⎟
⎟
⎟
⎠
,
φ
+
2
=
⎛
⎜
⎜
⎜
⎝
0.4881 + 0.0000i −0.0108 + 0.0041i 0.0063 + 0.0091i 0.4486 + 0.0509i
−0.0108 − 0.0041i 0.0216 + 0.0000i −0.0029 − 0.0066i −0.0140 − 0.0068i
0.0063 − 0.0091i −0.0029 + 0.0066i 0.0198 + 0.0000i 0.0044
− 0.0073i
0.4486 − 0.0509i −0.0140 + 0.0068i 0.0044 + 0.0073i 0.4706 + 0.0000i
⎞
⎟
⎟
⎟
⎠
,
φ
−
2
=
⎛
⎜
⎜
⎜
⎝
0.4911 + 0.0000i 0.0041 − 0.0184i 0.0058 + 0.0075i −0.4502 − 0.0462i
0.0041 + 0.0184i 0.0155 + 0.0000i 0.0005 + 0.0080i 0.0041 − 0.0089i
0.0058 − 0.0075i 0.0005 − 0.0080i 0.0209 + 0.0000i −0.0085 + 0.
0182i
−0.4502 + 0.0462i 0.0041 + 0.0089i −0.0085 − 0.0182i 0.4724 + 0.0000i
⎞
⎟
⎟
⎟
⎠
.
3. Tomography of the Bell state measurements
We analyze the efficiency of the measurement apparata. A BSM consists of Hang-Ou-Mandel (HOM) interferometers and
coincidence counts. The BSM is only partially deterministic, discriminating two of the four Bell states (|φ
±
or |ψ
±
) at a time.
The interferometry visibility in our setting is 0.91. Two BSM (1,2) are required to evaluate purity and overlap by measurements
on two system copies. This requires the indistinguishability of the four interfering photons 1–4, including their arriving time,
spatial mode, and frequency. As explained, our three source scheme ensures that, postselecting sixfold coincidences, each detected
photon pair is emitted by a different source. We test our measurement hardware by performing BSM tomography. The probe states
are chosen of the form |{H,V,D,A,R,L}
|{H,V,D,A,R,L}, where the labels identify the following photon polarizations:
horizontal (H), vertical (V), diagonal [D = (H + V)/
√
2], antidiagonal [A = (H − V)/
√
2], right circular [R = (H + iV)/
√
2],
and left circular [L = (H − iV)/
√
2]. The measurement results for all the possible outcomes are recorded accordingly. An iterative
maximum likelihood estimation algorithm yields the estimation of what projection is performed in each run [47]. The average
fidelities of BSM1 and BSM2 are 0.9389 ± 0.0030 and 0.9360 ± 0.0034, being the standard deviation calculated from 100 runs,
by assuming Poisson statistics. The estimated Bell state projections
1(2)
x
=|xx|
A
1
(B
1
)A
2
(B
2
)
,x = φ
±
,ψ
±
, reconstructed from
042327-5
![FIG. 1. Overlap detection. The network evaluates the overlap 〈e−iHnτ ρ2SeiHnτ 〉ρ1S , Hn = ∑n i=1 hi, in an n-qubit system S ≡ {Si}. Each pair of subsystem Si copies, in the state ρ1Si ⊗ ρ2Si , enters a two-arm channel (blue and green). The unitaries Uτ,i = e−ihi τ are applied to the second copy of each pair. Leaving both copies unperturbed, the network measures the state purity. The measurement apparatus (red) interferes each pair of subsystem copies byO(n) beam splitter gates UBS [20]. The overlap, and therefore the speed function in Eq. (4), is extracted by O(n) local detections.](/figures/fig-1-overlap-detection-the-network-evaluates-the-overlap-e-1wvpn0rh.png)

![TABLE II. Theoretical values. The table reports the theoretical values of the SLDF, which is the smallest quantum Fisher information (multiplying it by a constant turns it into the biggest one; see Sec. V), the lower bound Sτ (ρp,H2) [Eq. (4)], and the related entanglement witness conditions [Eq. (5)], for the Bell state mixture ρp and the spin Hamiltonians H2.](/figures/table-ii-theoretical-values-the-table-reports-the-zvtoaf8o.png)