The Astrophysical Journal, 784:13 (7pp), 2014 March 20 doi:10.1088/0004-637X/784/1/13
C
2014. The American Astronomical Society. All rights reserved. Printed in the U.S.A.
ELECTRON-IMPACT IONIZATION OF P-LIKE IONS FORMING Si-LIKE IONS
D.-H. Kwon
1
and D. W. Savin
2
1
Nuclear Data Center, Korea Atomic Energy Research Institute, Daejeon 305-353, Korea; hkwon@kaeri.re.kr
2
Columbia Astrophysics Laboratory, Columbia University, New York, NY 10027, USA
Received 2013 October 8; accepted 2014 February 4; published 2014 February 26
ABSTRACT
We have calculated electron-impact ionization (EII) for P-like systems from P to Zn
15+
forming Si-like ions. The
work was performed using the flexible atomic code (FAC) which is based on a distorted-wave approximation. All
3 → n
(n = 3–35) excitation-autoionization (EA) channels near the 3p direct ionization threshold and 2 → n
(n = 3–10) EA channels at the higher energies are included. Close attention has been paid to the detailed branching
ratios. Our calculated total EII cross sections are compared both with previous FAC calculations, which omitted
many of these EA channels, and with the available experimental results. Moreover, for Fe
11+
, we find that part
of the remaining discrepancies between our calculations and recent measurements can be accounted for by the
inclusion of the resonant excitation double autoionization process. Lastly, at the temperatures where each ion is
predicted to peak in abundances in collisional ionization equilibrium, the Maxwellian rate coefficients derived from
our calculations differ by 50%–7% from the previous FAC rate coefficients, with the difference decreasing with
increasing charge.
Key words: atomic data – atomic processes
1. INTRODUCTION
Modeling and interpreting spectra of collisionally ionized
astrophysical plasmas requires accurate calculations for the
underlying charge state distribution (CSD; Landi & Landini
1999; Kallman & Palmeri 2007; Bryans et al. 2009). Such
plasmas are formed in the Sun and other stars, supernova
remnants, the interstellar medium, galaxies, and the intracluster
medium in clusters of galaxies. These CSD calculations, in
turn, depend on reliable data for electron-ion recombination
and electron-impact ionization (EII). The past decade or so
has seen significant advances in the available theoretical and
experimental data for dielectronic recombination, which is
the dominant recombination process for most ions in cosmic
plasmas (Badnell 2006; Schippers et al. 2010). This is to be
contrasted with EII which theoretically has only recently been
comprehensively studied (Dere 2007). Experimentally, only in
the past few years have unambiguous laboratory r esults become
available (Hahn et al. 2011a, 2011b, 2012a, 2012b, 2013).
EII can occur through a number of different channels. Direct
ionization (DI) is a one-step process whereby an electron is
ejected from an ion A
q+
of charge state q+, for any gi ven
atom A, thereby forming an ion A
(q+1)+
. A number of two-step
processes can also contribute to EII. Excitation-autoionization
(EA) occurs when the incident electron excites a bound electron
to a level which can subsequently autoionize to form A
(q+1)+
or higher. The incident electron can also undergo dielectronic
capture (DC), forming a doubly excited A
(q−1)+
system which
can then undergo double autoionization, forming A
(q+1)+
.This
is known as resonant excitation double autoionization (REDA)
if the two electrons are released sequentially (LaGattuta &
Hahn 1981; Linkemann et al. 1995) and resonant excitation
auto double ionization (READI) if the two electrons are ejected
simultaneously (Henry et al. 1982; Pindzola & Griffin 1987;
Rinn et al. 1987).
EII calculations are theoretically challenging. They require
solving a Hamiltonian which include all the relevant interactions
in the scattering event. The potential form to use for the descrip-
tions of target and continuum electrons is often an issue. When
multi-step processes can be involved, a large number of interme-
diate states need to be accounted for along with their radiative
and autoionizing branching ratios (BRs). Additionally, the prob-
lem necessitates suitable wave function expansions both for the
target and continuum states. The most sophisticated method is
the close coupling (CC) approach, but this is computationally
expensive and unsuitable for generating the vast quantities of
data required in astrophysics. For this reason, the distorted wave
(DW) method has been most widely employed to generate EII
data for astrophysical plasma (Kallman & Palmeri 2007;Dere
2007).
Testing of these theoretical methods has been performed for
decades using benchmark experimental measurements. Reviews
of such work can be found in M
¨
uller (1990) and M
¨
uller (2008).
However until recently most laboratory measurements have
been limited to single pass experiments using ion beams with
an unknown population of metastable levels (e.g., Gregory
et al. 1987). As a result an exact comparison of theory with
experiment has not been possible for ions whose cross sections
differ between the metastable levels and the ground level.
The development of ion storage rings combined with merged
electron beams has helped to overcome this experimental
limitation. Using an ion storage ring one can store the ions
long enough so that for many systems essentially all of the
metastable levels can radiatively decay to their ground states.
The resulting EII data provide unambiguous benchmark data
for theory. To date, results from such experiments have been
published for Li-like Si
11+
and Cl
14+
(Kenntner et al. 1995),
Be-like S
12+
(Hahn et al. 2012b), B-like Mg
7+
(Hahn et al.
2010), F-like Fe
17+
and Ne-like Fe
16+
(Hahn et al. 2013), Na-like
Fe
15+
(Linkemann et al. 1995), Al-like Fe
13+
(Hahn et al. 2013),
Si-like Fe
12+
(Hahn et al. 2011b), P-like Fe
11+
(Hahn et al.
2011a), and S-like Fe
10+
and Cl-like Fe
9+
(Hahn et al. 2012a).
In Kwon & Savin (2012), we focused on comparing theory
and experiment for Fe
11+
. Previous experimental work by Hahn
et al. (2011a) had found discrepancies with the earlier theoretical
work of Dere (2007). The theory was below the experimental
results near the 3p DI threshold but above the measurements
at higher energies where innershell EA channels opened up.
1

The Astrophysical Journal, 784:13 (7pp), 2014 March 20 Kwon & Savin
TheworkofDere(2007) used the flexible atomic code (FAC)
of Gu (2008). In Kwon & Savin (2012) we also performed
FAC calculations, but took more channels into account. For that
work we included 3 → n
(n = 4–35) EA channels near the
threshold and the 2 → n
(n = 3–10) EA channels at higher
energies. Particular attention was paid to the detailed BRs. These
new FAC results helped to resolve several of the previously seen
discrepancies. Moreover, at temperatures where Fe
11+
forms in
collisional ionization equilibrium (CIE; Bryans et al. 2009)the
rate coefficient derived from our calculation lies within 11%
of the experimentally derived rate coefficient and is in better
agreement with the measurement of Hahn et al. (2011a) than
the previous FAC results of Dere (2007) which differed by up
to 25% from the measurement.
Here we have extended our EII calculations for Fe
11+
to
P-like systems from P to Zn
15+
. Moreover, for Fe
11+
in addition
to DI and EA we have also included the REDA process, which
we did not include in Kwon & Savin (2012). In Section 2,we
describe the calculational approach used to obtain theoretical EII
cross sections and rate coefficients. In Section 3 the calculated
total EII cross sections and rate coefficients are shown for the
selected ions and compared with available experiments and
with the previous theoretical works of Dere (2007). Lastly, we
summarize our results in Section 4.
2. THEORETICAL CALCULATIONS
We have calculated EII cross sections based on the approach
and ionization channels detailed in Kwon & Savin (2012). Here
we briefly review those calculations. In addition we describe the
method employed for calculating the Fe
11+
REDA cross section,
which was not part of Kwon & Savin (2012).
Here DI, EA and REDA are treated independently. The total
single ionization cross section can then be written as (Badnell
& Pindzola 1993)
σ
tot
=
f
σ
DI
f
+
j
σ
CE
j
B
a
j
+
k
¯σ
DC
k
B
da
k
, (1)
where σ
DI
f
is the DI cross section for any given ion A
q+
to
the level f of A
(q+1)+
. The second summation on the right hand
side of Equation (1) represents EA where σ
CE
j
is the collisional
excitation (CE) cross section of the initial A
q+
ions to level
j, which can then undergo autoionization by the emission of
a single electron to form A
(q+1)+
with a BR of B
a
j
. The third
summation is due to REDA where ¯σ
DC
k
is the energy averaged
DC cross section to level k of A
(q−1)+
, which can then double
autoionize, to form an A
(q+1)+
ionwithaBRofB
da
k
.
The BR for single autoionization of level j by emission of one
electron is given by
B
a
j
=
s
A
a
js
B
r
s
+
t
A
r
jt
B
a
t
s
A
a
js
+
t
A
r
jt
, (2)
where A
a
denotes the autoionization rate and A
r
denotes the
radiative decay rate. The s indices are for the levels of A
(q+1)+
and the t indices are for the levels of A
q+
. Some of the s levels
may lie above the ionization limit for A
(q+1)+
and some of the t
levels may lie above the ionization limit for A
q+
. The radiative
BR B
r
s
and autoionization BR B
a
s
account for the fraction of those
s and t levels eventually resulting in a net single ionization event.
Equation (2) must be solved recursively in order to determine
all of the BRs.
The BR for double autoionization of level k by emission of
two electrons can be expressed as
B
da
k
=
j
A
a
kj
B
a
j
j
A
a
kj
+
t
A
r
kt
, (3)
where A
a
kj
is the autoionization rate of A
(q−1)+
from k to any
level j
of A
q+
, A
r
kt
is the radiative decay rate of A
(q−1)+
from
k to t
, and B
a
j
is the BR for autoionization of j
level given by
Equation (2).
In order to compare the theoretical REDA results with
experimental data we need to define the energy averaged DC
cross section ¯σ
DC
k
. This smooths over the resonances in the DC
cross section σ
k
and can be related to the experimental energy
spread by
¯σ
DC
k
=
σ
k
v
v
0
, (4)
where the numerator is defined as
σ
k
v=
σ
k
(v)vf (v
0
, v)d
3
v. (5)
Here v
0
is the average longitudinal center-of-mass electron
velocity in the experiment and v is the electron velocity vector
relative to the ions. The term σ
k
v can be expressed analytically
as Equation (9) of Kilgus et al. (1992) for the “flattened”
Maxwellian distribution typical of ion storage rings, as we
discuss more in the results section. In that equation, following
the theoretical framework of Shore (1969), the integrated cross
section of state k for DC can be expressed as
ˆσ
k
=
2π¯h
R
E
k
πa
2
0
g
k
2g
i
A
a
ik
, (6)
where ¯h is the Planck constant divided by 2π ;
R is the Rydberg
energy constant; E
k
denotes the resonance energy; a
0
is the Bohr
radius; g
k
and g
i
are the statistical weights of the captured and
initial states, respectively; and A
a
ik
is the autoionization rate
from the level i to k.
The ionization channels for DI and EA considered here
are the same as those of Kwon & Savin (2012) for Fe
11+
forming Fe
12+
except that we have included some additional
EA channels and autoionization decay channels resulting in net
double ionization which are energetically viable for some ions
with low atomic number Z.ForP,S
+
,Cl
2+
,Ar
3+
, and K
4+
the
3 → n
EA channels open up at threshold for the ground
state from n = 3 but for the isoelectronic Ca
5+
–Zn
15+
the 3 EA
channels open up starting from n = 4. In addition for P, S
+
, and
Cl
2+
,the2 → 3
EA channel followed by autoionization
to 2[s, p]
8
3[s, p]
3
3d levels can further autoionize to form
Al-like ions since some of the 2[s, p]
8
3[s, p]
3
3d levels lie above
the Si-like ionization threshold. Here n[s, p]
m
indicates that m
electrons are distributed between the s and p orbitals in the
n shell. However, these autoionizing levels in the Si-like ions
are below the Si-like ionization limit for initially Ar
3+
–Zn
15+
systems, thereby resulting in no net double ionization. Lastly
DI of a 2 electron of the initial P-like system was not included
because we calculate that the resulting 2-hole system for P-like
ions considered will autoionize over 93% of the time to form
Al-like ions.
In addition to the above, we also calculated REDA for Fe
11+
.
The REDA channels included are as follows. The first step
proceeds via the DC process
e
−
+2s
2
2p
6
3s
2
3p
34
S
3/2
→ 2[s, p]
7
3s
2
3p
3
n
1
1
n
2
2
, (7)
2
The Astrophysical Journal, 784:13 (7pp), 2014 March 20 Kwon & Savin
where for n
1
= 3, n
2
= 4–30 and for n
1
= 4, n
2
= 4. For all
cases
1
<n
1
and
2
5 were included. The DC cross sections
for 2 → n
1
1
with n
1
> 4 were so small that they can be
neglected. The captured states can autoionize by emitting one
electron to form Fe
11+
via
2[s, p]
7
3s
2
3p
3
n
1
1
n
2
2
→
⎧
⎪
⎨
⎪
⎩
2[s, p]
8
3[s, p]
4
n
3
3
2[s, p]
8
3[s, p]
3
n
1
1
n
2
2
2[s, p]
7
3[s, p]
5
n
3
3
⎫
⎪
⎬
⎪
⎭
+ e
−
,
(8)
or can radiatively decay leaving the system as Fe
10+
by
2[s, p]
7
3s
2
3p
3
n
1
1
n
2
2
→
2[s, p]
8
3[s, p]
4
n
1
1
n
2
2
2[s, p]
8
3s
2
3p
3
n
3
3
+ hν.
(9)
The autoionizing states in Equation (8) can then sequentially
emit another electron to form Fe
12+
⎧
⎪
⎨
⎪
⎩
2[s, p]
8
3[s, p]
4
n
3
3
2[s, p]
8
3[s, p]
3
n
1
1
n
2
2
2[s, p]
7
3[s, p]
5
n
3
3
⎫
⎪
⎬
⎪
⎭
→ 2[s, p]
8
3[s, p]
4
3[s, p]
3
n
3
3
+ e
−
,
(10)
or radiatively decay via
⎧
⎪
⎨
⎪
⎩
2[s, p]
8
3[s, p]
4
n
3
3
2[s, p]
8
3[s, p]
3
n
1
1
n
2
2
2[s, p]
7
3[s, p]
5
n
3
3
⎫
⎪
⎬
⎪
⎭
→ 2[s, p]
8
⎧
⎪
⎨
⎪
⎩
3[s, p]
5
3[s, p]
4
n
3
3
3[s, p]
3
n
1
1
2
⎫
⎪
⎬
⎪
⎭
+hν.
(11)
For 2 → 3
1
excitation and capture into n
2
> 30, a simple
hydrogenic scaling law (Romanik 1988) was used to extrapolate
the resonance energies, autoionization rates, and radiative decay
rates of the captured electrons. In the extrapolation the resonance
energy for t he captured states of n
2
> 30 is given by
E
k
(n
2
) = E
k
(n
s
) − (Z − N +1)
2
1
n
2
2
−
1
n
2
s
R (12)
for n
s
= 30 since the binding energy for high n
2
Rydberg levels
can be expressed as
−
(Z − N +1)
2
(n
2
− δ)
2
R −
(Z − N +1)
2
n
2
2
R, (13)
where the quantum defect δ is independent of n
2
and n
2
δ
(Cowan 1981). The autoionization and radiative decay rates are
given by
A
a
kj
(n
2
) = A
a
kj
(n
s
) ×
n
3
s
n
3
2
(14)
and by
A
r
kt
(n
2
) = A
r
kt
(n
s
) ×
n
3
s
n
3
2
, (15)
respectively. The radiative decay rate of the core electron for
these higher n
2
levels was set to that of the last n
2
= 30 level
for which explicit calculations were carried out.
Based on the good agreement found in Kwon & Savin (2012)
with the experimental results, we used the post form of a V
N
potential where N is the number of initial target electrons
(Pindzola et al. 1995). In the DW approximation, the cross
section is obtained by considering the continuum and bound
electrons interactions perturbatively. For the first order pertur-
bation t heory used in the conventional DW approach, the inter-
action potential is taken as a Coulomb field generated from an
arbitrary effective charge, due to the screening of the nucleus
by the continuum and bound electrons, and neglecting the long
range interaction between the scattered and ejected continuum
electrons (Macek & Botero 1992). Hence, the validity of the
assumed potential form in DW relies on benchmarking by ex-
perimental results (Pindzola et al. 1995). This is to be contrasted
with the more sophisticated CC method where the interaction
is treated non-perturbatively, taking into account long-range,
three-body Coulomb effects. Clearly a more exact treatment for
the potential, for example, using the time-dependent CC ap-
proach (Pindzola & Schulz 1996), would be helpful to further
verify the proper potential form choice.
More specifically, a single local central potential for the ini-
tial and final state radial wave functions was optimized on the
3s
2
3p
3
configuration of initial target ion for DI, EA, and REDA.
The alternative optimization on the 3s3p
3
+3s
2
3p
2
configura-
tions can lead to different values for the cross section, especially
for DI. The sensitivity of the results to the configuration selected
increases as the charge state of the initial target ion decreases.
However, as we show below, optimization on the 3 s
2
3p
3
config-
uration yielded good agreement with the available experimental
results for S
+
,Cl
2+
, and Ar
3+
as well as for Fe
11+
. Hence that
is the configuration we selected for optimizing the radial wave
functions.
For a Maxwell–Boltzmann electron energy distribution at
an electron temperature T
e
, the DI and EA rate coefficient
α
DI+EA
(T
e
) is generated from the calculated cross section σ (E)
using
α
DI+EA
(T
e
) =
1
(m
e
π)
1/2
2
k
B
T
e
3/2
×
∞
0
σ
DI+EA
(E)exp
−
E
k
B
T
e
dE, (16)
where k
B
is the Boltzmann constant and m
e
is the electron mass.
For REDA the Maxwellian rate coefficient is given by (Shore
1969)
α
REDA
(T
e
) =
1
2g
i
4πa
2
0
R
k
B
T
e
3/2
k
g
k
A
a
ik
B
da
k
exp
−
E
k
k
B
T
e
.
(17)
Adding these two gives the total ionization rate coefficient
α
I
(T
e
) = α
DI+EA
(T
e
)+α
REDA
(T
e
). (18)
3. RESULTS
The calculated DI+EA+REDA cross section for ground state
Fe
11+
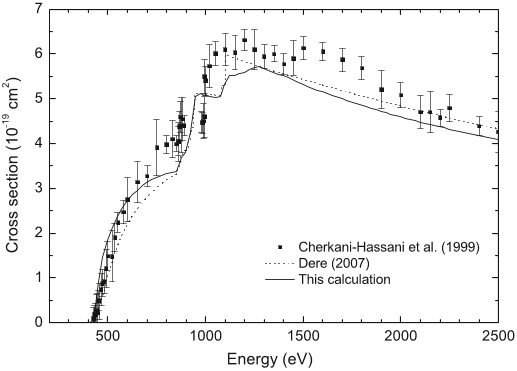
is shown in Figure 1. In order to compare our REDA
results with ion storage ring data, we must convolve the
theoretical data with the flattened Maxwellian distribution of
the experiment, which is described by parallel T
and transverse
T
⊥
temperatures with respect to the electron beam direction
(Schippers et al. 2001). For Fe
11+
these were k
B
T
= 13.5meV
and k
B
T
⊥
= 180 μeV (Hahn et al. 2011a).
In our previous EII calculation for ground state Fe
11+
(Kwon
&Savin2012), the 2 → 3
EA channel appeared to turn on
about 20 eV higher in energy than the experimental data. We hy-
pothesized that this difference could be due to neither REDA nor
READI being accounted for in our previous calculations. As can
be seen in Figure 1, including the REDA leads to better agree-
ment with the experiment between ∼680 and 720 eV. H owever
3

The Astrophysical Journal, 784:13 (7pp), 2014 March 20 Kwon & Savin
Figure 1. FAC calculations for the EII cross section for ground state Fe
11+
including the DI+EA+REDA contributions. The solid line represents the
calculated total EII cross section including the REDA cross section and the
dashed line shows the DI+EA cross sections. Also shown are the experimental
results of Hahn et al. (2011a). The experimental data are plotted using large filled
circles and their 1σ experimental uncertainty is shown by the small points.
Figure 2. Our calculated EII cross section for ground state P forming P
+
is
compared with the available experimental results. Various choices for the local
central potential for DI are plotted in different line types. The large error bar
shows the total experimental systematic uncertainty.
the theory is still below the experiment in the energy range
720–800 eV. This remaining discrepancy is unlikely to be due
to REDA. It is true that over the energy range of 640–920 eV DC
can proceed via e
−
+2 → n
1
1
n
2
2
(n
1
= 3 or 4 and n
2
> 3).
But there are many more sizable resonances concentrated in the
energy range 640–750 eV than in the energy range 750–920 eV
and the convolved REDA cross section is significant only in
the energy range 640–750 eV as shown in Figure 1.Wemay
attribute the remaining difference between theory and experi-
ment over the energy range 720–800 eV to READI which has
not yet been incorporated into FAC and therefore has not been
considered here. In the energy range of 405–920 eV, READI can
occur energetically for DC via e
−
+2 → n
1
1
n
2
2
(n
1
= 3or
4 and n
2
3). The detailed READI cross section calculation is
beyond the scope of this paper. READI has been considered for
Li-like systems using many-body perturbation theory (Pindzola
&Griffin1987) and a unified R-matrix approach (M
¨
uller 2000;
Scott et al. 2000). However, it is unclear how to relate those
results to the more complex P-like systems considered here.
Figure 3. Same as Figure 2 but for ground state S
+
forming S
2+
. The small error
bars show the statistical deviations of the measurements, and the large error bar
shows the total experimental systematic uncertainty.
Figure 4. Same as Figure 3 but for ground state Cl
2+
forming Cl
3+
.
The REDA contribution to the Maxwellian rate coefficient
increases the DI+EA rate coefficient by less than 4% at temper-
atures where Fe
11+
is predicted to form in CIE. This is only a
small contribution to the total EII rate coefficient, and so we do
not include REDA in the calculated total EII cross sections and
rate coefficients for all the P-like ions from P to Zn
15+
presented
below.
Figures 2–6 show our calculated total EII cross sections for
some selected other P-like ions where experimental data is
available to compare with. As for comparison to the FAC results
of Dere (2007), he did not present data for P, S
+
, and Cl
2+
.His
FAC calculations for Ar
3+
and Ni
13+
are shown in Figures 5
and 6, respectively.
Figure 2 shows our calculated cross section for P. At the peak,
it is up to two times larger than the measurements of Freund et al.
(1990). At the highest energies it is in good agreement with
experiment. The agreement does not improve if we use other
potentials for the calculations. Using the V
N−1
potential for DI
optimized on the 3s3p
3
+3s
2
3p
2
configurations reduces both the
peak cross section as well as that at high energies. Similarly, the
agreement is also poor using a V
N
+ V
N−1
potential optimized
on the 3s
2
3p
3
+3s3p
3
+3s
2
3p
2
configurations.
The cause for the discrepancy between experiment and theory
is not immediately obvious. The neutral atoms in the experiment
4

The Astrophysical Journal, 784:13 (7pp), 2014 March 20 Kwon & Savin
Figure 5. Same as Figure 3 but for ground state Ar
3+
forming Ar
4+
.Alsoshown
are the previous FAC results from Dere (2007).
were generated using charge-transfer neutralization of fast
P
+
. The resulting neutral beam had an unknown metastable
population. Clearly, measurements on ground state P would
greatly help to resolve the issue by providing unambiguous
laboratory benchmark data. Moreover, such benchmark results,
could guide the selection of the proper potential form to use for
DW calculations.
Another theoretical issue which may play a role involves
the approximations used for the calculation of the collision
cross section. FAC assumes a weak interaction in order to
derive the scattering matrix (Bar-Shalom et al. 1988;Gu2008;
Sampson et al. 2009). Such an approach is usually reliable
for highly charged ions but breaks down for neutral atoms.
This approximation does not ensure that the scattering matrix
is unitary, which implies potentially incomplete conservation
of wave function flux before and after scattering. This issue
is generally corrected for using a normalization procedure
(Sobelman et al. 1981;Clark1990). Unfortunately the correction
is not implemented at present in FAC. Alternatively, it is possible
that calculations with the more sophisticated CC R-matrix
method, which should yield a scattering matrix closer to unitary,
might resolve the discrepancy between experiment and theory.
Our new FAC calculations for S
+
are in good agreement with
the measurements by Yamada et al. (1988) and Djuri
´
cetal.
(1993) near the ionization threshold and also at peak as shown
in Figure 3. But at higher energies our calculations agree better
with the results of Djuri
´
cetal.(1993) than with those of Yamada
et al. (1988).
For Cl
2+
our new FAC calculations are in good agreement with
the measurement by Mueller et al. (1985) near the ionization
threshold and also at peak as shown in Figure 4. At higher
energies our calculation is lower than the measurement but still
within the total experimental systematic uncertainty.
Figure 5 shows our new FAC calculations for Ar
3+
. At peak
energy they are in better agreement with the measurements by
Gregory et al. (1983) than with those by M
¨
uller et al. (1980).
At an energy of ∼60 eV, near the 3 ionization threshold, our
calculated total EII cross section, which includes EA via 3 into
high n
, is in better agreement with the experimental data of
Gregory et al. (1983) than are the FAC cross section results by
Dere (2007).
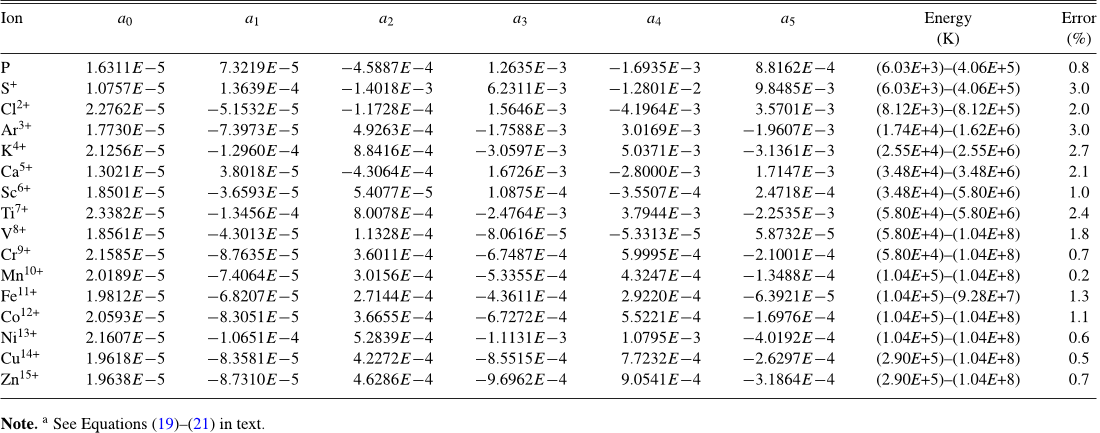
Our new FAC calculation for Ni
13+
near the ionization
threshold is in better agreement with the measurement by
Figure 6. Same as Figure 5 but for ground state Ni
13+
forming Ni
14+
.
Figure 7. EII rate coefficients for various ground state P-like ions forming
Si-like ions. The solid line represents our FAC results and the dotted line shows
the FAC result by Dere (2007), except for S
+
. The dotted line for S
+
is the BT
scaled fit derived from the measurement by Yamada et al. (1988). For Fe
11+
the
experimental rate coefficient of Hahn et al. (2011a) is also shown by the dashed
line. The horizontal bars show the CIE temperature regime predicted by Bryans
et al. (2009) where each ion is over 1% abundant.
Cherkani-Hassani et al. (2001) than are the previous FAC results
by Dere (2007), as can be seen in Figure 6. However our
calculated cross section lies below the measurement at energies
of ∼840–2000 eV where 2 → n
EA contributes. Resolving
these discrepancies would be greatly aided by laboratory EII
measurements on ground state Ni
13+
.
Surprisingly, for EII of S
+
–Ar
3+
the metastable contamina-
tion in the experimental results seems to generate no major
discrepancies between our calculations and the laboratory data.
We attribute this, in part, to the fact that the metastable states
have the same 3s
2
3p
3
valence shell configuration as that of the
ground state (See Gregory et al. 1983). According to our calcu-
lations, DI is the dominant contribution to the EII cross section
for all P-like systems from P through Zn
15+
. We find that the
peak DI cross sections for the metastable levels are larger by
only 8% for S
+
compared to the ground state. This decreases to
4% by the time one reaches Ar
3+
. However, for P the increase is
22%, much larger than for S
+
–Ar
3+
. This decreasing difference
with increasing Z is due to decrease in the importance of
electron–electron interactions as the nuclear charge increases.
5