




read more










The authors can think of two avenues for further research. On the one hand, the activation and deactivation of the safety task as well as a dynamic exchange of task priority roles can induce some chattering phenomena, which can be avoided by introducing a hysteresis scheme. Secondly, the dimensionality of the subspace associated to each null space projector is a necessary condition to be considered when designing subtasks, however it might not be sufficient to guarantee the fulfilment of the subtask and a thorough analytical study of these spaces can be required.
The addition of more tasks in cascade is possible as long as there exist remaining DoF from the concatenation of tasks higher up in the hierarchy.
The visual servo mission task requires 6 DoF, and the secondary and comfort tasks with lower priority can take advantage of the remaining 4 DoF.
1) Primary task: Among all other tasks, the one with the highest priority must be the safety task, not to compromise the platform integrity.
The gravitational vector alignment task and the joint limits avoidance task require 1 DoF each being scalar cost functions to minimize (see Eq. 35 and 43).
The desired task variable is σ∗L = 0 (i.e. σ̃L = −σL), while the corresponding task Jacobian isJL = [ 01×4 −2 (ΛL (qa − q∗a))> ] . (45)One common choice of q∗a for the joint limit avoidance is the middle of the joint limit ranges (if this configuration is far from kinematic singularities), q∗a = qa + 1 2 (qa − qa).
Finally the dynamics of the system can be written as[ σ̇0 σ̇1 ] = [ −Λ0 O −J1J+0 Λ0 −Λ1 ] [ σ0 σ1 ] , (29)which is characterized by a Hurwitz matrix as in [23] that guarantees the exponential stability of the system.
This guarantees asymptotic stability of the control law regardless of the target point selection, as long as planar configurations are avoided.
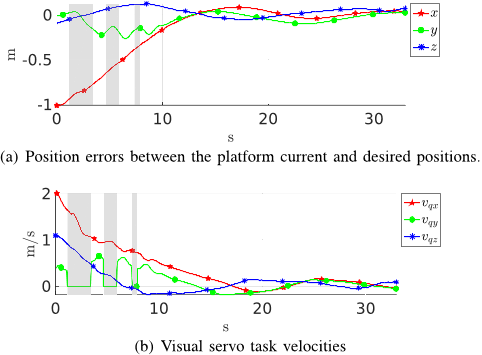
When the obstacle does not violate the inflation radius, the safety task becomes deactivated and the other subtasks can regain access to the previously blocked DoF. Fig. 3(a) shows how the servoing task is elusive during the first 10 seconds of the simulation when the obstacle is present, but is accomplished afterwards when the obstacle is no longer an impediment to the secondary task.
Ja q̇a = R c b Ja q̇a, (11)with Rcb the rotation matrix of the body frame with respect to the camera frame, and where vcq corresponds to the velocity of the quadrotor expressed in the camera framevcq = R c b[ νbq + ω b q × rbcωbq] = [ Rcb −Rcb [ rbc ] ×0 Rcb] vbq, (12)with rbc(qa) the distance vector between the body and camera frames, and vbq = [νqx, νqy, νqz, ωqx, ωqy, ωqz]> the velocity vector of the quadrotor in the body frame.
for the primary task the authors can substitute Eq. 21 into Eq. 20, giving σ̇0 = Λ0σ̃0, which for a defined main task error σ̃0 = σ∗0 − σ0 and σ∗0 = 0, the asymptotic stability is proven with L̇ = −σT0 Λ0σ0.
By denoting with JI , JS , JG and JL theJacobian matrices of the above-mentioned tasks, the desired system velocity can be written as followsq̇ = J#I σ̃I + NI J # S ΛSσ̃S + NI|S J + G σ̃G+NI|S|G J + L σ̃L − JI|S|G|L$, (30)where NI , NI|S , NI|S|G are the projectors of the safety, the visual servoing and of the center of gravity tasks, which are defined asNI = (I− J#I JI) (31a) NI|S = (I− J+I|S JI|S) (31b) NI|S|G = (I− J+I|S|G JI|S|G) , (31c)with JI|S and JI|S|G the augmented Jacobians computed as in Eq. 27.
The sum of normalized distances of the position of the i-th joint to its desired configuration is given bym∑ i=1 ( qai − q∗ai qai − qai )2 . (42)So their task function is selected as the squared distance of the whole arm joint configuration with respect to the desired oneσL = (qa − q∗a)>ΛL (qa − q∗a), (43)where qa = [ qa1, . . . , qam ]> and q a = [ q a1 , . . . , q am ]> are the high and low joint-limit vectors respectively, and ΛL is a diagonal matrix whose diagonal elements are equal to the inverse of the squared joint limit rangesΛL = diag((qa1 − qa1) −2, . . . , (qam − qam) −2). (44)
The generalization of Eq. 23 to the case of η prioritized subtasks isq̇ = J+0 Λ0σ̃0 + η∑ i=1 N0|...|i−1J + i Λiσ̃i − J0|...|η$ (24)with the recursively-defined compensating matrixJ0|...|η = N0|...|i−1J + i Ji +