Rashba spin precession in a magnetic field
Jun Wang,
1,2
H. B. Sun,
1
and D. Y. Xing
2
1
Center of Quantum Computing Technology and School of Physical Sciences, University of Queensland, Brisbane Qld 4072, Australia
2
National Laboratory of Solid State Microstructures and Department of Physics, Nanjing University, Nanjing 210093, China
共Received 11 August 2003; published 11 February 2004兲
Spin precession due to Rashba spin-orbit coupling in a two-dimension electron gas is the basis for the spin
field effect transistor, in which the overall perfect spin-polarized current modulation could be acquired. There
is a prerequisite, however, that a strong transverse confinement potential should be imposed on the electron gas
or the width of the confined quantum well must be narrow. We propose relieving this rather strict limitation by
applying an external magnetic field perpendicular to the plane of the electron gas because the effect of the
magnetic field on the conductance of the system is equivalent to the enhancement of the lateral confining
potential. Our results show that the applied magnetic field has little effect on the spin precession length or
period although in this case Rashba spin-orbit coupling could lead to a Zeeman-type spin splitting of the energy
band.
DOI: 10.1103/PhysRevB.69.085304 PACS number共s兲: 73.21.⫺b, 71.70.Ej, 73.40.Sx
Spin-polarized electron transport in microstructures has
attracted considerable attention since last decade, fueled by
the possibility of producing efficient photoemitters with a
high degree of polarization of the electron beam 共spin light-
emitting diode兲, creating spin-based memory device and uti-
lizing the properties of spin coherence for quantum compu-
tation and communication. In the spintronics 共spin-based
electronics兲 field, both degree of freedom of spin and charge
are exploited, even spin could entirely replace the electric
charge to carry information. This is the basis for a new gen-
eration of electric devices.
1
The spin-polarized field effect transistor 共SFET兲 proposed
by Datta and Das
2
is one of the most attractive spintronic
devices for it may switch faster than the traditional transistor
since it can avoid redistributing charges during operation.
The idea is based on Rashba spin-orbit 共RSO兲 coupling
3
in
two-dimensional electron gas 共2DEG兲. It results in spin pre-
cession as electrons move along a heterostructure and can be
controlled by an external electric field. This novel spintronic
device has three requirements: 共1兲 long spin-relaxation time
in 2DEG; 共2兲 gate voltage control of RSO coupling, and 共3兲
high spin injection efficiency. At present, the first two con-
ditions have been basically satisfied in experiments.
4,5
It ap-
pears to be very difficult, however, to achieve an efficient
injection of spin-polarized carriers from a ferromagnetic
metal into 2DEG, and a great deal of work has been dedi-
cated to this challenge.
6–11
Apart from the three requirements above for an SFET, in
fact, there is another basic limitation to the ultimate imple-
mentation of SFET, i.e., in order to restrict the angular dis-
tribution of electrons in a 2DEG,
2
a strong enough transverse
confining potential must be imposed on the 2DEG or the
width of the confined quantum well must be very narrow.
The RSO interaction in the 2DEG comes from the inversion
asymmetry of the structure and can be expressed as
3
H
R
⫽ (
␣
/ប)(
⫻ p), where
is Pauli matrix,
␣
is the RSO cou-
pling constant proportional to the external electric field E,
and p is the momentum operator. The term H
R
itself can lift
the degeneracy of spin space but not lead to a Zeeman-type
split of energy band, because the time inversion symmetry of
system remains unchangeable under this RSO interaction.
When an electron propagates, however, the RSO coupling
can result in spin precession of electronic current along its
propagating way due to the interference of two spin-splitting
electronic waves. To ensure the perfect spin modulation of
electric current in SFET, the energy gap between two neigh-
boring subbands due to the lateral confining potential, which
is generally assumed to have reflection symmetry, must be
much larger than the intersubband mixing from RSO
coupling,
2,12
i.e.,
具
n
兩
H
R
兩
n⫹ 1
典
/(
n⫹1
⫺
n
)Ⰶ 1 with n being
the index of subband. Therefore, the subband energy disper-
sion from RSO keeps linear k dependence. It has been
argued
12
that in the hard-wall confining potential, the width
of the quantum well must satisfy WⰆប
2
/
␣
m with m being
the effective mass of electrons. From this, one can see that
the RSO coupling constant
␣
modulated by an external elec-
tric field is strongly limited by the width W of transverse
confined potential well.
In this paper, we propose to employ an external magnetic
field to relieve the limitation to a strong transverse confining
potential or the narrow well width. The Landau level will
form in the magnetic field so that the energy gap of intersub-
bands could be enlarged and the RSO coupling constant
␣
could be modulated in a larger range, in which the perfect
spin-current modulation could not be destroyed. The mag-
netic field effect is equivalent to the enhancement of the
confining potential or the reduction of the effective width of
the quantum wire. However, does it introduce another factor
to destroy the spin precession? To answer this question is
another motive of this paper that investigates the interplay
between the RSO coupling and the external magnetic field.
Our numerical results show that the RSO coupling in mag-
netic field will lead to spin split of the subband spectrum like
Zeeman effect, while the spin precession from RSO coupling
keeps almost invariable such as its length or period.
The model we adopted is a two-terminal device that a
quasi-one-dimensional quantum wire with RSO coupling is
connected by two ideal leads. This device is subjected to a
magnetic field perpendicular to the two-dimensional plane
共xy plane, it is assumed that x is the current direction of the
PHYSICAL REVIEW B 69, 085304 共2004兲
0163-1829/2004/69共8兲/085304共5兲/$22.50 ©2004 The American Physical Society69 085304-1

device兲. Considering the real condition in experiment, the
magnetic field applied to the RSO coupling region is as-
sumed inhomogeneous and being tuned adiabatically on and
off as in Ref. 13. After discreting procedure, a type of tight-
binding Hamiltonian including the RSO coupling on a square
lattice is obtained in absence of magnetic field,
12
H⫽
兺
lm
lm
C
lm
†
C
lm
⫺ t
兺
lm
兵
C
l⫹ 1,m
†
C
lm
⫹ C
l,m⫹ 1,
†
C
lm
⫹ H.c
其
⫺ t
so
兺
lm
⬘
兵
C
l⫹ 1,m,
⬘
†
共
i
y
兲
⬘
C
lm
⫺ C
l,m⫹ 1,
⬘
†
共
i
x
兲
⬘
C
lm
⫹ H.c.
其
, 共1兲
where C
lm
†
(C
lm
) is the creation 共annihilation兲 operator of
electron at site 共lm兲 with spin
and
lm
⫽ 4t is the site-
energy, t⫽ប
2
/2ma
2
is the hopping energy, a is the lattice
constant, and t
so
⫽
␣
/2a is the RSO coupling strength. Here
we focus on the case of an impurity-free quantum wire with
RSO coupling. The generalization to the case including im-
purities is straightforward.
14
In our following calculation, all
energy is normalized by the hoping energy t(t⫽ 1). When
the magnetic field B(0,0,1) is introduced, it could be incor-
porated into the nearest-neighbor hopping energy by the
Peierl’s phase factor such as
T
lm,lm⫹ 1
⫽ t exp
共
iប
c
l/2t
兲
⫽
共
T
lm⫹ 1,lm
兲
쐓
;T
lm,l⫹ 1,m
⫽
共
T
l⫹ 1m,lm
兲
쐓
⫽ t, 共2兲
where
c
⫽ eB/mc is the cyclotron frequency. We choose
vector potential A(By,0,0) and keep the transitional symme-
try of system along the x direction 共electric current direc-
tion兲. In magnetic field, RSO coupling Hamiltonian is reex-
pressed as H
R
⫽ (
␣
/ប)
⫻ (p⫹ eA/c) so that t
so
has a
similar modification. The spin-quantum axis is chosen along
z direction. The Zeeman effect from the external magnetic
field is not included here.
In the ballistic transport, the conductance of structure is
given by Landauer-Buttiker formula G
⫽ (e
2
/h)T
and T
is the multichannel transmission coefficient of electron with
spin
. Based upon the nonequilibrium Green function
formalism,
15
the following result for spin-resolved conduc-
tance is obtained
14
G
⬘
⫽
e
2
h
Tr
关
⌫
L
G
r
⬘
⌫
R
⬘
G
a
⬘
兴
, 共3兲
where ⌫
L(R)
⫽ i
关
⌺
L(R)
r
⫺ ⌺
L(R)
a
兴
, ⌺
L(R)
r
⫽ (⌺
L(R)
a
)
쐓
is the self
energy from the left 共right兲 lead, G
r(a)
is the retarded 共ad-
vanced兲 Green function of the structure, and the lead effect is
incorporated into the self energy of green function G
r(a)
.
The trace is over the spatial degrees of freedom. The Green
function above is computed by the well-known recursive
Green function method
16,17
and the conductance is evaluated
at the Fermi energy. Our following discussion is based on the
assumption that only spin-up polarized electrons are injected
from the left lead into RSO region 共where the spin preces-
sion of incident electron is induced兲 and collected in the right
lead.
We have chosen the lattice size a much smaller than the
Fermi wavelength
F
(
F
⫽ 10a) so that our model can
simulate a continuum system. The width and the length of
the quantum wire are taken as N
y
a⫽ 30a and N
x
a⫽ 60a,
respectively. The calculated results of the conductance are
plotted in Fig. 1 as a function of the external magnetic field
in the absence of RSO interaction. It appears that the con-
ductance is quantized and decreases with magnetic field. At
បw
c
⫽ 0, there are 6 modes 共subbands兲 at the Fermi energy
(E
F
⫽ 0.4t) contributing to the conductance. When បw
c
⫽0,
all subbands are elevated and the energy gap of intersub-
bands increases due to the formation of Landau level as
shown in Fig. 2 共more detailed later兲. The transmitted modes
below E
F
thus becomes less and the conductance is quan-
tized and decreases with B. Basically, when បw
c
⬎ 2E
F
,
there is no transmitted mode contributing to conductance and
it decreases to zero. The conductance quantization induced
by magnetic field resembles that found in quantum point
contact, in which the number of modes at E
F
will change in
discrete steps by constricting continuously its width.
18
In
other word, the magnetic field effect on the conductance of a
quantum wire is equivalent to the reduction of its effective
width or enhancement of the confining potential because a
strong transverse potential will also lead to decrease of the
number of modes at E
F
.
19
Apart from the quantization of conductance in Fig. 1, an-
other character, the oscillation of conductance is also found
in our results. This oscillation is referred to as the Aharonov-
Bohm 共AB兲 effect
20,21
and originates from the edge state
22
in
a magnetic field. Due to the multireflection of electrons in
quantum wire before they escape to the collector, the right-
going channel and left-going channel form a loop resulting
from the perpendicular magnetic field so that the quantum
interference will lead to AB effect as that in a mesoscopic
ring. The oscillation periodicity is related to the wave vector
of the transmitted mode and the length of the multireflection
region. Consequently, the oscillation becomes apparent just
FIG. 1. The conductance of quantum wire as a function of mag-
netic field ប
c
in absence of RSO coupling t
so
⫽ 0. The inset en-
larges the points just above the threshold of the second transmitted
mode.
WANG, SUN, AND XING PHYSICAL REVIEW B 69, 085304 共2004兲
085304-2

above the threshold of every transmitted mode where the
wave vector turns out to be smaller.
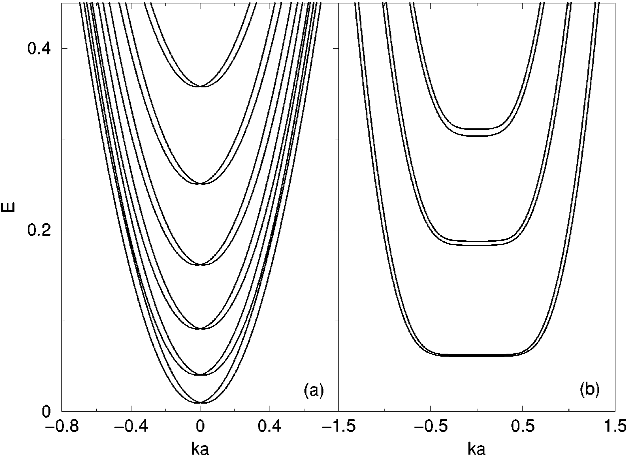
The subband energy spectrum is plotted in Fig. 2 at the
presence of RSO coupling. Since the contribution to conduc-
tance of those evanescent modes could be neglected, only
these modes at E
F
are shown. When there is no magnetic
field B⫽ 0 in Fig. 2共a兲, the spectra seem to be simple para-
bolic due to a weak RSO coupling t
so
⫽ 0.02t used in our
calculation.
19
The degeneracy of spin space is lifted by the
RSO coupling, however, it does not resemble Zeeman effect
that leads to split of the energy band, and here the spin de-
generacy at k⫽0 still exists. When the intersubband mixing
from RSO coupling is neglected, the spin-resolved eigenval-
ues are approximately at every subband
⫾
(k)⫽
n
⫹ ប
2
k
2
/2m⫾
␣
k, ⫾ denotes two spin-splitting bands due to
the RSO coupling and not the eigenstates of
z
yet. Once
B⫽0, the Landau levels form in the system and this is the
reason of the platform appearing at the bottom of subbands
共near k⫽ 0) as shown in Fig. 2共b兲. Both the subbands and
their energy difference are enhanced in comparison with Fig.
2共a兲 when the external magnetic field increases, moreover,
the gap of intersubbands is basically equivalent to បw
c
.Itis
interesting to note that the RSO coupling will lead to a
Zeeman-type energy-band split under B⫽0. In an ideal
2DEG under a magnetic field, the plane waves of eigenstates
have no group velocity,
/
k⫽ 0, and the RSO modifica-
tion has no relation with wave vector k. At this moment, the
difference of the two spin eigenvalues is ⌬
⫽ (2
␣
冑
2m/ប)
冑
បw
c
(n⫹ 1), here n denotes the Landau
level. Thus the RSO spin-splitting strength is related to the
energy level index n and the magnetic field B.
The effect of an external magnetic field is equivalent to
the enhancement of the transverse confining potential on a
quantum wire, which results in an enlargement of the inter-
subband energy gap so that the perfect spin-polarized current
modulation can be kept in a larger
␣
parameter region. In
Fig. 3, two spin-splitted conductances are presented as the
RSO coupling strength t
so
varies. At B⫽ 0, the conductance
modulation is quickly and clearly weakened by the intersub-
band mixing that increases with RSO coupling; otherwise, as
B increases, the subband mixing from RSO coupling could
be neglected compared to the intersubband energy gap, and
the perfect spin modulation of conductance would remain in
a larger RSO coupling range as shown in Fig. 3共b兲, where
FIG. 2. The subband energy spectrum with
RSO coupling strength t
so
⫽ 0.02; 共a兲 no mag-
netic field ប
c
⫽ 0 and 共b兲ប
c
⫽ 0.24.
FIG. 3. The spin modulation of conductance vs RSO coupling
strength t
so
; the solid line and dash line represent G
↑↑
and G
↑↓
,
respectively. 共a兲ប
c
⫽ 0 and 共b兲ប
c
⫽ 0.40.
RASHBA SPIN PRECESSION IN A MAGNETIC FIELD PHYSICAL REVIEW B 69, 085304 共2004兲
085304-3

only one transmitted mode contributing to conductance is
chosen to be plotted as a result of the magnetic field effect.
This oscillation of conductance originates from the interfer-
ence of two RSO spin-splitted electronic waves in one sub-
band. The oscillation period can be determined by the accu-
mulated phase difference ⌬
⫽ 2t
so
*
N
x
, here N
x
a is the
length of RSO interaction region. For instance, N
x
⫽ 60 is
chosen in our calculation and the oscillation period is esti-
mated T
t
s0
⫽ 0.512. The RSO coupling is the basic principle
for the operation of an SFET. One can control the output spin
polarization of the SFET by tuning the RSO coupling con-
stant via an external electric field. In a real device, it is also
required that spin dephasing length should be much longer
than device size to avoid spin mixing. While in order to
avoid the distraction of spin modulation at the collector by
the intersubband mixing, an external magnetic field may be
an alternative as discussed above.
Another point to be noted is that even B⫽0, the oscilla-
tion period from RSO coupling is still independent of the
energy of injected electrons and the magnetic field, i.e., two
spin-resolved conductances are mainly determined by the
RSO coupling constant
␣
and the length of RSO region N
x
a,
when the number of mode at E
F
is fixed. In Fig. 4, we plot
the conductances as a function of magnetic field at different
␣
and N
x
. It is shown that the conductance G
↑
and G
↓
keep
almost unvaried as the magnetic field B varies. This case is
similar to that they are independent of the energy of injected
electrons at a weak RSO coupling region unless the different
transmitted modes at Fermi energy are involved 共not shown兲
when the energy of injected electrons varies.
12
In summary, we have investigated the ballistic transport of
a quasi-one-dimensional quantum wire considering the RSO
interaction under an external magnetic field. We find that the
perfect spin modulation of the conductance due to the RSO
coupling would not be destroyed in the large coupling con-
stant region because the RSO coupling between different
transmitted modes is negligible compared with their energy
difference. We conclude that our proposal of applying a mag-
netic field to the system can be a proper alternative to the
prerequisite of the narrow width of the quantum wire or the
strong transverse confining potential for the functional opera-
tion of a spin field effect transistor.
This work was supported by Australian Research Council
under Project LX0347471; D.Y.X. thanks the state key pro-
grams for Basic Research of China for financial support un-
der Grant No. 10174011.
1
See, e.g., M. Oestreich, Nature 共London兲 402, 735 共1999兲; S.A.
Wolf, D.D. Awschalom, R.A. Buhrman, J.M. Daughton, S. von
Molna
´
r, M.L. Roukes, A.Y. Chtchelkanova, and D.M. Treger,
Science 294, 1488 共2001兲.
2
S. Datta and B. Das, Appl. Phys. Lett. 56, 665 共1990兲.
3
Y.A. Bychkov and E.I. Rashba, J. Phys. C 17, 6039 共1984兲.
4
J.M. Kikkawa and D.D. Awschalom, Phys. Rev. Lett. 80, 4313
共1998兲.
5
J. Nitta, T. Akazaki, H. Takayanagi, and T. Enoki, Phys. Rev. Lett.
78, 1335 共1997兲.
6
C.-M. Hu and T. Matsuyama, Phys. Rev. Lett. 87, 066803 共2001兲;
D. Grundler, ibid. 86, 1058 共2001兲.
7
T. Matsuyama, C.-M. Hu, D. Grundler, G. Meier, and U. Merkt,
Phys. Rev. B 65, 155322 共2002兲; P. Mavropoulos, O. Wunnicke,
and Peter H. Dederichs, ibid. 66, 024416 共2002兲.
8
G. Schmidt, D. Ferrand, L.W. Molenkamp, A.T. Filip, and B.J.
van Wees, Phys. Rev. B 62, R4790 共2000兲; E.I. Rashba, ibid. 62,
R16 267 共2000兲; J.D. Albrecht and D.L. Smith, ibid. 66, 113303
共2002兲.
9
A.T. Hanbicki, B.T. Jonker, G. Itskos, G. Kioseoglou, and A.
Petrou, Appl. Phys. Lett. 80, 1240 共2002兲; V.F. Motsuyi, J. De
Boeck, J. Das, W. Van Roy, G. Borghs, E. Goovaerts, and V.I.
Safarov, ibid. 81, 265 共2002兲.
10
R. Fiederling, M. Keim, G. Reuscher, W. Ossau, G. Schmidt, A.
Waag, and L.W. Molenkamp, Nature 共London兲 402, 787 共1999兲;
Y. Ohno, D.K. Young, B. Beschoten, F. Matsukura, H. Ohno,
and D.D. Awschalom, ibid. 402, 790 共1999兲.
11
G. Kirczenow, Phys. Rev. B 63, 054422 共2001兲.
12
F. Mireles and G. Kirczenow, Phys. Rev. B 64, 024426 共2001兲.
13
Z.L. Ji and D.W.L. Sprung, Phys. Rev. B 54, 8044 共1996兲.
14
T.P. Pareek and P. Bruno, Phys. Rev. B 65, 241305 共2002兲; L.W.
Molenkamp, G. Schmidt, and G.E.W. Bauer, ibid. 62, 4790
共2000兲.
15
L.V. Keldysh, Sov. Phys. JETP 20, 1018 共1965兲.
16
P.A. Lee and D.S. Fisher, Phys. Rev. Lett. 47, 882 共1981兲.
17
T. Ando, Phys. Rev. B 44, 8017 共1991兲; M.J. Mclennan, Y. Lee,
and S. Datta, ibid. 43, 13846 共1991兲; H.U. Baranger, D.P. Divin-
cenzo, R.A. Jalaber, and A.D. Stone, ibid. 44, 10637 共1991兲.
FIG. 4. The spin-resolved conductance in different RSO cou-
pling constants t
so
and the lengths of quantum wire N
x
; the solid
line and dash line are same as in Fig. 3. 共a兲 t
so
⫽ 0.02, N
x
⫽ 60;
共b兲 t
so
⫽ 0.04, N
x
⫽ 60; 共c兲 t
so
⫽ 0.02, N
x
⫽ 40, t
so
⫽ 0.04, N
x
⫽ 40.
WANG, SUN, AND XING PHYSICAL REVIEW B 69, 085304 共2004兲
085304-4

18
B.J. van Wees, H. van Houten, C.W.J. Beenakker, J.G. William-
son, L.P. Kouwenhoven, D. van der Marel, and C.T. Foxon,
Phys. Rev. Lett. 60, 848 共1988兲.
19
A.V. Moroz and C.H.W. Barnes, Phys. Rev. B 60, 14272 共1999兲.
20
H. Yoshioka and Y. Nagaoka, J. Phys. Soc. Jpn. 59, 2884 共1990兲.
21
Y. Takagaki and D.K. Ferry, Phys. Rev. B 47, 9913 共1993兲.
22
A.G. Scherbakov, E.N. Bogachek, and U. Landman, Phys. Rev. B
53, 4054 共1996兲.
RASHBA SPIN PRECESSION IN A MAGNETIC FIELD PHYSICAL REVIEW B 69, 085304 共2004兲
085304-5