Correlation and convolution filtering and image
processing for pitch evaluation of 2D micro- and
nano-scale gratings and lattices
XIAOMEI CHEN
1,*
, LUDGER KOENDERS
2
, SIMON PARKINSON
3
1
Centre for Autonomous & Cyber-Physical System, Cranfield University, Cranfield MK43 0JR, UK
2
Surface Metrology Department, Physikalisch-Technische Bundesanstalt(PTB), Bundesallee 100, 38116 Braunschweig, Germany
3
School of Computing, University of Huddersfield, Queensgate, HD1 4DH Huddersfield, West Yorkshire, UK
*Corresponding author: xiaomei.chen@cranfield.ac.uk
Received XX Month XXXX; revised XX Month, XXXX; accepted XX Month XXXX; posted XX Month XXXX (Doc. ID XXXXX); published XX Month XXXX
We have mathematically explicated and experimentally demonstrated how a correlation and convolution filter can
dramatically suppress the noise that coexists with the scanned topographic signals of 2D gratings and lattices with
2-dimensional (2D) perspectives. To realize pitch evaluation, the true peaks’ coordinates have been precisely
acquired after detecting the local maxima from the filtered signal, followed by image processing. The combination
of 2D filtering, local-maxima detecting and image processing make up the pitch detection (PD) method. It is
elucidated that the pitch average, uniformity, rotation angle and orthogonal angle can be calculated using the PD-
method. This has been applied to the pitch evaluation of several 2D gratings and lattices, and the results are
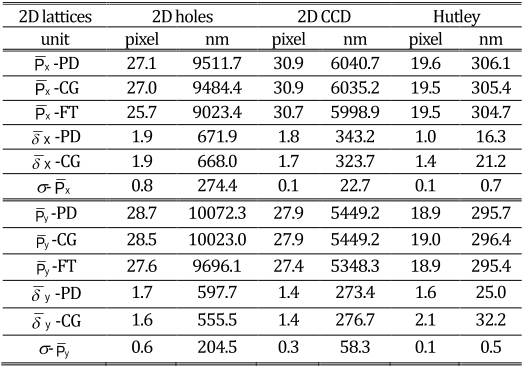
compared with the results of using the CG- and FT-method. The differences of pitch averages which are produced
using the PD-, CG- and FT-methods are within 1.5 pixels. Moreover, the PD-method has also been applied to detect
the dense peaks of Si (111) 7×7 surface and the HOPG basal plane.© 2015 Optical Society of America
OCIS codes: (120.0120) Instrumentation, measurement, and metrology; (100.0110) Imaging processing; (070.6110) Spatial filtering; (180.0180)
Microscopy.
http://dx.doi.org/10.1364/AO.99.099999
NOMENCLATURE
CC
Correlation
and convolution;correlation or convolution
XYZ
or
XOY
3D or 2Dcoordinate
s
systemof samplesurface
xyzorxoy 3D/2D coordinates of measuring instrument, e.g. an SPM
ϕ
x
,
ϕ
y
The angles thatXOY plane tilts relative tox-and y-axis of
xyzsystem
P
X
, P
Y
Pitches ofa 2D grating or lattice, and periodsofits
topographicsignal
f
(
X
,
Y
)
in
XYZ
system
P
x
, P
y
Projections of P
X
and P
Y
in xoy plane: P
x
=
P
X
⋅
cos
ϕ
x
,
P
y
=P
Y
⋅cos
ϕ
y
∆x,∆y
Scanning step sizesof an SPMin x- and y-axis
p
x
, p
y
Computer-sampleddata numberswithin P
x
and P
y
periods
Pq,Pr Periodsof a half2Dsinusoidal waveform
∆
q ,
∆
r
Element intervalsofa half2Dsinusoidal waveform
p
q
, p
r
Element numberswithin PqandPr periods
1. INTRODUCTION
The pitch described in this paper is the distance between adjacent
similar structural features of one-dimensional (1D) and two-
dimensional (2D) gratings and lattices on surfaces. In nanometer
metrology and measurement, the International Organization for
Standardization (ISO) stipulates 1D and 2D gratings and lattices in
several documents to calibrate diverse microscopes and instruments
after metrologically verifying the pitch-related parameters, such as
pitch average, pitch uniformity, etc. Microscopes and instruments
include a family of scanning probe microscopes (SPM) [1], scanning
electron microscopes (SEM) [2,3], various optical microscopes and
contact stylus instruments that are used for areal surface roughness
measurement [4,5]. Usually, metrological atomic force microscopes
(AFM) and nano-measuring machines (NMM) [6-8] implement the
metrological verification. This typically includes two steps: acquiring
the three-coordinate topographic signal in raster-scan mode, and
afterwards evaluating the pitch-related parameters according to a
pitchevaluationmethod.
Beside the center-of-gravity (CG) method [9,10] and Fourier-
transform-based (FT) method [10], another pitch evaluation method
of 1D gratings based on a 1D correlation filter has been previously
published [11,12]. A half 1D sinusoidal waveform sequence with
period P
T
is taken as a correlation filter. When it cross-correlates with a
1D grating topographic signal with period P, the noise can be greatly
suppressed if P
T
≈P. After correlation filtering, the distance between
any two adjacent waveform peaks, along the direction perpendicular
to 1D grating lines, is one pitch. The method was described as the peak
© 2017 Optical Society of America. One print or electronic copy may be made for personal use only. Systematic reproduction and distribution, duplication
of any material in this paper for a fee or for commercial purposes, or modifications of the content of this paper are prohibited.
This is the Author Accepted Manuscript issued with: Creative Commons Attribution Non-Commercial License (CC:BY:NC 4.0).
The final published version (version of record) is available online at DOI:10.1364/AO.56.002434.
Please refer to any applicable publisher terms of use.
Applied Optics, 2017, Volume 56, Issue 9, pp2434-2443
DOI:10.1364/AO.56.002434

detection (PD) method. The pitch average, uniformity and rotation
anglearound z-axiscan be calculated using the PD-method.
It has always been cumbersome to evaluate the pitches of 2D
gratings and lattices based on CG- and FT-methods. The 2D gratings
and lattices (defined by XOY plane) are mounted on the stage (defined
by xoy plane) of the measuring instrument to be subsequently raster-
scanned into images. When raster-scanning only a cluster of 2D grating
or lattice features into image, we will find that the grating and lattice
structures are always orientating an unknown
θ
angle around z-axis
relative to the xoy plane. The unknown
θ
angle, plus the accompanied
noise, will make the CG- and FT-method performance more
demanding and less correct. In order to avoid the
θ
angle, the strategy
is to make sure that the
θ
angle in the xoy plane is minimized to zero (
θ
≈ 0°). To achieve this, the 2D grating or lattice that has been loaded
onto the xoy plane, needs to be located, orientated, image-scanned and
image-analyzed to determine if the raster-scan lines are parallel to any
assumed line that passes through a series of gravity centers of the 2D
grating or lattice. The above actions have to be iteratively repeated
until
θ
≈0°. Regardless of the size, the raster-scan area is indispensable
[13] for metrologically verifying a 2D grating or lattice on a
metrological AFM or a NMM, as well as applying it as a standard
material to metrologically calibrate an SPM [14], and to map its errors
[15,16] in accordance with ISO standards [17]. Except for CG- and FT-
methods, there is an absence of literature addressing the problem in
2D pitch evaluation methods. Therefore, our intention is to apply the
PD-method to the pitch evaluation of 2D gratings and lattices by
suppressing the noise and making the
θ
angle known, so that the CD-
and FT-method can be precisely fulfilled with decreasing workload.
Commercially available software [18] has taken a unit cell of
topographic signals from 2D gratings and lattices as the template to
calculate the 2D correlation average. In this paper, a half 2D sinusoidal
waveform is proposed as a template for all features of 2D gratings and
lattices. It can achieve the equivalent impact and high credibility for
analyzing the images and topographic signals containing repeated 3D
structural features. Furthermore, the template as a CC filter can
dramatically suppress the noise and greatly improve the signal-to-
noise-ratio (SNR), consequently the positions and orientations of 3D
features can be precisely characterized andmeasured.
For identifying positions and locations of the repeated structural
features on diverse surfaces [19-22], others have applied a grayscale
threshold segmentation to binarize images, and edge and centroid
detection to extract the borders and locate the centers. In contrast, we
will introduce the 2D CC filter and the peak detection based on local-
maxima detecting and image processing for identifying the peak
positions of 2D gratings and lattices. To the best of our knowledge, the
binary and ternary image reconstruction procedure presented in the
paper is unique. Finally, the mathematical explanation of the 2D CC
filtering, as well as the practicalalgorithm to determine the periods of a
2D half sinusoidalwaveform templatehavebeenannexed.
2. 2D SINUSOIDAL GRATING
A. Topographic and coexisted signals
When an SPM or a scanning tunneling microscope (STM) raster-
scans a 2D sinusoidal grating along two orthogonal direction x and y at
the step size ∆x and ∆y, it crosses the X- and Y-pitches, P
X
and P
Y
, of the
2D sinusoidal grating with an unknown
θ
angle. The raster-scanned
2D signal F(x,y) (in such physical units as length, voltage, current, etc.),
against the positions (x,y) can be decomposed as a 2D sinusoidal
topographic signal f(x,y), a nonlinear drift signal U(x,y) and a noise
signal W(x,y), i.e.
(
)
(
)
(
)
(
)
, , , ,
F x y f x y U x y W x y
= + +
(1)
Coordinate x and y, signal F(x,y), f(x,y), U(x,y) and W(x,y) are all M ×N
matrices in a raster-scan range M∆x × N∆y. An example signal of a 2D
sinusoidal grating with 300 nm nominal pitches, F(x,y), is shown by a
2D intensity graphin Fig. 1(a).
It is supposed that theorigin of XYZ coincideswiththat of xyz. Due to
the existence of a 2D nonlinear drift signal U(x,y), the XOY plane tilts a
ϕ
x
angle relative to x-axis and
ϕ
y
angle relative to y-axis. If the 2D
sinusoidal topographic signal,inXYZ systemis defined by
2 2
sin sin( )
, .
X Y
X Y
A
P P
f X Y
π π
=
(2)
It isexpressed inxyz system as
2 ( cos sin ) 2 ( sin cos )
sin sin
cos cos
2 ( cos sin ) 2 ( sin cos )
sin sin
( ),
,
X x Y y
x y
x y x y
A
P P
x y x y
P P
f x
A
y
π θ θ π θ θ
ϕ ϕ
π θ θ π θ θ
− +
− +
=
=
(3)
where, 1) X=(xcos
θ
−ysin
θ
)/cos
ϕ
x
and Y=(xsin
θ
+ycos
θ
)/cos
ϕ
y
means
that the coordinates first rotate-transform by an
θ
angle from the XOY
coordinates (of the 2D sinusoidalgrating)to the xoy coordinates(of the
measurement instrument), subsequently rotate-transform by
ϕ
x
angle
around the x-axisand
ϕ
y
angle around the y-axis respectively; 2) The X-
and Y-axes are parallel to the direction of the X-pitch and Y-pitch, P
X
and P
Y
, respectively; 3) P
x
=P
X
cos
ϕ
x
and P
y
=P
Y
cos
ϕ
y
mean the
projectionsofP
X
and P
Y
in the xoy plane.
U(x,y), according to ISO/DIS 11952[17], is presumably caused by
piezo drift or creep in lateral or vertical direction; mechanical stresses
of the sample holders and its fixers; mechanical expansion of the
components such as measurement frame of an SPM. The diminishing
effect on the accurate pitch evaluation can be leveled by rotation-
transforming
ϕ
x
and
ϕ
y
angles around the x- and y-axis respectively, so
that U(X,Y) ≈0 in XYZ system, which means the drift signal theoretically
does not exist in XYZ system. Mathematically, it is expressed by a 2D
polynomial function in the xyz system whether it has been leveled or
unleveled:
1 1
,
( ) ( ) ( ) .
TU
K
K K
x y c a x b y a x b y
R = + + + + +L
(4)
where, c=a
0
+b
0
is the content item, a
i
and b
i
(i=1,2, …, K) are the
coefficientsof theith order item of variable x and y , respectively.
W(x,y) is given by the amplitude a
x,y
at any raster-scanposition (x,y):
,
( , ) .
x y
W x y
a
=
(5)
B. 2D CC-filtered signals
A half 2D sinusoidal waveform template T(q, r) with Pq and Pr
periods is described by
2 2
( ) sin sin
, .
q
r
q r
T q B
P P
r
π π
=
(6)
T(q,r) has a matrix of M
T
×N
T
elements against a matrix of M
T
×N
T
positions (q,r)with intervals ∆qand ∆r.
The correlation or convolution between F(x,y) and T(q,r) is
expressed by
, , , ,
( ) ( ) ( ) ( ).
TF Tf TU TWR R R R
x y x y x y x y
= + +
(7)

(a) (b) (c)
Fig. 1. (a),(b)and (c)shows 2Dsinusoidal grating topographicsignalF(x, y),correlation-filteredsignalR
TF
(x,y) and peaksdetection image in intensity graphs, respectively.
Fig.2. Based on convolution operation, 3D plots of filtered topographic signalR
TF
(x,y) (without normalization) with periods Px=Py=20 pixels; figure a, b, c, d, e and f are
corresponding to Pq=Pr=P/4,P/2,P,2P, 3Pand 4P, respectively .
R
TF
(x,y), R
Tf
(x,y), R
TU
(x,y) and R
TW
(x,y) are named as filtered signal,
filtered topographic signal, filtered nonlinear drift signal and noise
residue signal, respectively.
If correlation operator (+) and convolution operator (−) are
combined into one operator (±), R
Tf
(x,y), R
TU
(x,y) and R
TW
(x,y) in xyz
system is developed as equation (8), (9) and (10), respectively. The
mathematical developments are listedin Annex A.
2 (
[ ] [ ]sin( [ ])
cos
2 (
sin( [ ])
cos
cos sin )
( , )
sin cos )
.
X
Y
Tf q r X q
x
Y r
y
x y
C P D P P
P
x y
P
P
R x y
π
φ
ϕ
π
φ
ϕ
θ θ
θ θ
= +
⋅ +
−
+
(8)
1
1 1
,( ) ( ) ( ) .TU K
K
K K
J J Jx y a x b y a x b yR = + + + + +L
(9)
1 1
,
0 0
( ),( )
( ) ,,
T T
TW
M N
k l
k l
x k q y l r
R x Ay a
− −
= =
± ∆ ± ∆
= ⋅
∑ ∑
(10)
where, C[Pq] and
φ
X
[Pq] are concerned with Pq whilst D[Pr] and
φ
Y
[Pr]
are related with Pr. They are defined by equation (A.3) ∼ (A.6) in the
Annex A. J is the constant item; J
1
, J
2
,⋅⋅⋅, J
K
are the weighted index of
monomial item, quadratic item, …, and Kth order item of the binary
polynomials, respectively. They are explained by equation (A.8)
∼ (A.10) in Annex A.
Compared with equation (3), equation (8) verifies that R
Tf
(x,y)
remains a 2D sinusoidal signal. Its periods, P
x
and P
y
, are equal to the
periods of f(x,y), though the amplitude has changed to C[Pq]D[Pr] and
phases have shiftedto
φ
X
[Pq] and
φ
Y
[Pr].
Compared with equation (4), equation (9) interprets that R
TU
(x,y)
still is a nonlinear drift signal. It will not disturb the peaks detection
even if it is unleveled beforehand, or if it is not totally diminished after
leveled.
In contrast to equation (5), equation (10) is the operation of
weighted moving average (WMA) of the noise signal a
x,y
by using a
matrix of data A
k,l
(k=0, 1, ..., M
T
-1, l=0, 1, ..., N
T
-1) as the weights. A
k,l
is
expressed by equation (A.12) in AnnexA.

Therefore, after correlation or convolution (CC) filtering, the noise
signal a
x,y
, from highly dense irregularities, is minimized to a small and
gently changing noise residue signal R
TW
(x,y). Although it can more or
less modulate the amplitude of the R
Tf
(x,y) if it is superimposed to the
latter, it does not influence the periodicity of the latter (see Fig. 3
ref.[12]).
An 80×80 2D sinusoidal simulation signal f(x,y) of 1 arbitrary unit
(a.u.) amplitude and 20 a.u. periods (Px=Py=20), with Gaussian white
noise W(x,y) of 0.3 a.u. standard deviation, was taken as an example to
demonstrate how R
TF
(x,y) varies with period Pq and Pr of a half 2D
sinusoidal waveform template T(q,r). T(q,r) has 1 a.u. amplitude and
M
T
×N
T
elements, where M
T
=Pq/2, N
T
=Pr/2. Based on convolution
operation, the 3D plots of R
TF
(x,y) are shown in Fig. 2, where 3D plots
markedby a,b, c, d, e and f correspond to Pq=Pr=P/4, P/2, P, 2P, 3P and
4P,which are 5,10, 20, 40, 60 and 80 a.u., respectively.
From a half 1D sinusoidal waveform as 1D cross-correlation filter
[11,12], when a half 2D sinusoidal waveform of Pq and Pr periods
correlates or convolutes with the raster-scanned signal of a 2D
sinusoidal grating of P
x
and P
y
periods withnoise, we candeduce:
(1) itcan greatly filter noise if Pq≈P
x
and Pr ≈P
y
;
(2) itcannot completely filter noise if Pq <<P
x
;
(3) it can filter noise but severely modulate the amplitude of signal
R
Tf
(x,y) to make it impossible to distinguish R
Tf
(x,y) from
R
TW
(x,y) if Pq >>P
x
andPr>>P
y
.
Thus, instead of directly detecting the pitches from the raster-
scanned signal F(x,y), the filtered signal R
TF
(x,y) is validated for the
pitch detection if we chose Pq≈P
x
and Pr≈P
y
. For 2D sinusoidal grating
signal F(x,y) shown in Fig. 1(a), the correlation-filtered signal R
TF
(x,y) is
exhibited in 2D intensity graph in Fig. 1(b). The practical algorithm on
how to choose Pq and Pr to implement the CC filtering is attached in
AnnexB.
3. 2D LATTICES
A 2D lattice is a repetitive arrangement of 3D features, such as
pillars, hills, holes, dimples, etc. The 3D convex type features have
parallelogram (rectangle, square, diamond, etc.) or circle bottoms and
the 3D concave type features have parallelogram or circletops. Lattices
are fabricated such that the features are arranged in square,
rectangular, hexagonal and oblique array. The arrangement is in
similarity to 2D solid crystalline lattices. Mathematically, they are
described bydifferent analytic functions inside and zero outside the 3D
features.
A. Topographic signals
For a P
x
- and P
y
-pitch lattice with any 3D feature in square,
rectangular, hexagonal, and oblique array, the raster-scanned
topographic signal (with P
x
- and P
y
-periods) is defined as f(x,y) inside
the 2D waveforms and zero outside. A primitive unit cell witha bottom
or top area A can be defined in the rectangular range G{-P
x
/2≤x≤P
x
/2, -
P
y
/2≤y≤P
y
/2} so that the 3D feature waveforms at the origin lies
entirely within the primitive unit bottom or top, where x and y are two
independent real variables in the whole feature array.The topographic
signal of two exemplar square lattices with 3D central-symmetric
features in parallelogram holes and hills is shown in Fig. 3(a) and (b),
respectively.
The topographic signal of a lattice can be developed as a 2D Fourier
series incomplexexponential form:
,
( , ) [ exp[ ( )].I JIJ
I J
x yf x y A j x y
ω ω
∞
=−∞
= ⋅ +
∑
(11)
where,
ω
xI
= 2πI/P
x
and
ω
yJ
= 2πJ/P
y
are the angularfrequencyin x- and
y-axes, respectively; A
IJ
is the Fourier transformation coefficient given
by
1
( , )exp[ ( )]d d ,
( , 1, 2, ).
xI yJ
IJ
G
A f x y j x y
G
I J
ω ω
= − +
= ± ± ⋅⋅⋅
∫∫
(12)
(a) (b)
(c) (d)
Fig. 3. Topographic signals of square lattices with 3D features in parallelogram
holesand hillsin (a) and (b); the correspondent correlation filtered signals are in
(c) and(d) respectively.
To expand Equation (11) as the real form (Annex C), we find that
2D signal f(x,y) consists of four group of 2D sinusoidal signals with
different phase shifts in each group. Each group includes a constant
item (I, J=0) and infinite numbers of 2D sinusoidal signals including a
fundamental (I, J = 1) period P
x
and P
y
, and harmonic period P
x
/I and
P
y
/J (I, J = 2, 3, 4,···). Since the amplitude A
IJ
decreases sharply with I
and J increasing [25], the sinusoidal waveform in fundamental period
(I,J=1) dominates equation (11). Concerning the square lattices with
such 3D central symmetric features as shown in Fig. 3 (a) and (b),
equation (11) can be simplified as
, 0
( , ) 4 sin( )sin( )
2 2
I JIJ
I J
x yf x y A x y
π π
ω ω
∞
=
= − −
∑
(13)
B. 2D CC-filtered signals
If a half 2D sinusoidal waveform with period Pq≈P
x
and Pr≈P
y
is
usedtofiltera series of 2D sinusoidal signals of 2D lattice (with periods
P
x
/I and P
y
/J expressed by equation (13)). The filtered 2D sinusoidal
signal with fundamental periods (I, J=1) has the same period P
x
and P
y
.
The filtered 2D sinusoidal signals with harmonic periods, due to
Pq >>P
x
/I and Pr >>P
y
/J (I,J=2,3,4···), have been severely modulated.
Moreover, with periods decreasing (i.e. I and J increasing), their
amplitudes sharply dropped. Therefore, when the filtered 2D
sinusoidal signals with fundamental and harmonic periods are
combined into the filtered signal of 2D lattices, the filtered 2D
sinusoidal signal infundamentalperiodsdominates.

The images of the 2D square holes and 2D hills in square arrays in
Fig. 3 (a) and (b) are raster-scanned by different types of AFM in
256×256 pixels. The actual raster-scan ranges are 90µm×90µm and
50µm×50µm, respectively. After correlation-filtered using a half 2D
sinusoidal waveform with periods, p
q
and p
r
of 30 pixels and 40 pixels,
the filtered signals are plotted as 2D intensity graphs in Fig. 3 (c) and
(d), respectively.
4. AUTOMATIC PEAK DETECTION
The peak detection in R
TF
(x,y) can be performed as follows. If a data
R
TF
(m,n) at (m,n) (m=0,1, ..., M-1, n=0,1, ..., N-1) position in M×N matrix
signal is the true peak, it is the local maximum in both row m and
column n. First, two M×N zero matrices B
R
and B
C
are constructed.
Based on the algorithm to find the local maxima in a sequence signals
by applying quadratic/parabolic interpolation of three adjacent
samples [23, 24], the following two steps are taken to detect the local
maxima from row vectors and column vectors, respectively.
Subsequently, the new values are assigned to the corresponding
positionsin B
R
and B
C
, respectively:
(1) The local maxima of R
TF
(m,n) are detected row by row. If
R
TF
(m,n) is detected as a local maximum in row m, B
R
(m,n) is
converted to 1, otherwise it remains 0.
(2) The local maxima of R
TF
(m,n) are detected column by column.
If R
TF
(m,n) is detected as a local maximum in the column n,
Bc(m,n) isconverted to 1, otherwise it remains0.
As a result, B
R
and B
C
are dual-value M×N matrices. Apparently,
R
TU
(x,y) and R
TW
(x,y) do not influence the local maxima detection,
though they are included in R
TF
(x,y). If a data item R
TF
(m,n) is a true
peak, it should be grey-scale 1 in both images, i.e. B
R
(m,n)=B
C
(m,n)=1.
However, if it is only a local maxima, either B
R
(m,n)=1, B
C
(m,n)=0 or
B
R
(m,n)=0, B
C
(m,n)=1. If B
R
and B
C
are merged into a new image G
E
using logical ‘AND’ or arithmetical ‘add’ of the corresponding pixels, G
E
consists of 0 and 1 or 0, 1 and 2 values. The former is called binary
image and the latter is called ternary image. Those pixels with grey-
scale 1 in the binary image G
E
or grey-scale 2 in the ternary image G
E
are the true peaks. Thus, a ternary images is displayed in dark
background (grayscale=0), colored pixels (grayscale=1) and bright
pixels (grayscale=2). The local maxima (grey-scale=1), which have
disappeared in the binary image, can produce good visual effect in the
ternary image to associate the peaks with the original and filtered
images.
The peaks detection to the raster-scanned signal of the 2D
sinusoidal grating in Fig. 1(a) is shown bythe ternary image in Fig.1 (c).
The peak detection of the signals in Fig.3 is shown in Fig. 4. Where, (a)
and (b) are the ternary images before 2D correlation filtering. They
appear chaotic and disordered due to noise; (c) and (d) are the ternary
images after 2D correlation filtering. The true peaks in bright pixels
with grayscale 2 can be easily extracted from the ternary images Fig. 4
(c) and (d).
The peak detection process was applied to the raster-scanned
signals of 2D atomic lattices: (1) silicon (111)-7×7 scanned by the
variable temperature scanning tunneling microscope (VT STM) in
30nm×30 nm range and 800×800 pixel density shown in Fig. 5 (a); (2)
HOPG scanned by the VT STM in 10nm ×10 nm range and 150×150
pixel density shown in Fig. 6 (a). As a result, the correlation-filtered
signals (p
q
=p
r
=30 and 10 pixels, respectively) and the ternary images
including true peaks and local maxima are shown in Fig. 5 (b) and (c)
as well as Fig 6 (b) and (c), respectively. It is made possible to use
atoms positions and unit cells to detect the directional drift of the
sample, i.e., the motion of the scanner in an STM.
(a)
(b)
(c) (d)
Fig. 4. Ternary image (a), (b), (c) and (d) are the peak detection results
correspondingtothe topographic signal (a) and (b),correlationfilteredsignal (c)
and(d)inFig.3, respectively.
(a) (b) (c)